近年の情報社会におけるコンピュータビジュアリゼーションの研究 〜視覚効果に着目した高度な画像表現・情報提示技術〜
東京大学大学院新領域創成科学研究科 複雑理工学専攻 高橋 成雄 准教授

ボリュームデータと伝達関数

伝達関数とは、ボリュームレンダリングで中身を可視化するために使う、色と透明度に一回変換する関数です。

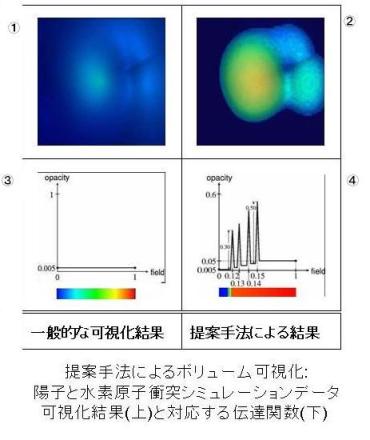
図2は、陽子と水素原子の衝突直後のデータです。これに対して、数値データの特徴（分布）を何も考えない伝達関数で可視化すると、真ん中が明るくなる結果になります。（図2-1）
これじゃ、どうしようもないんで、特徴解析したものがこれです。（図2-2）このデータに対して、等値面の閾値を高い値から低くしていくと、2つの球がでてきて、くっついて1回イビツなドーナツを作って、穴となり、最後は穴が埋まって大きな塊になります。こういう形状のトポロジーに関する特徴点をとりだし伝達関数を設定すると、図2-4のような伝達関数が設計できます。
実は、これでシミュレーションした方がいらっしゃって、お見せした時のフィードバックが結構面白く、彼らは、水素原子と陽子がここら辺にあるということは知っていたんですけども、このときにエネルギーがどこを回って戻ってきているっていうのは全然、認識していなかったのですが、これをみて、それがはっきりしたそうです。これは可視化が、人間が普通気付かないような情報をきちんと拾い出して、見えないものをきちんとユーザに提示してくれた一つの例ですね。

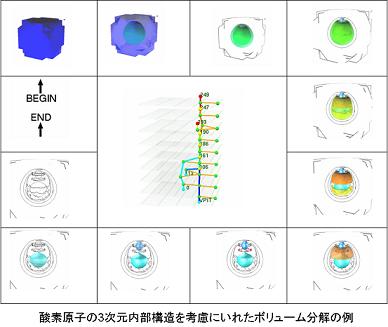
図3は、別のボリュームデータの入れ子構造に着目し、分解したものです。
中央のグラフは、等値面のトポロジー変化を示すもので、ここから、この下向きになる部分は片側が入れ子になっていることがわかります。このグラフだけ抽出できれば、入れ子関係が分かるのでこの部分が内側になるんだから、こっちのほうに大きな不透明度を与えてやって、そうすると外側が少しうすく透けていって内側のほうが良く見える、ということができます。
このグラフは操作のインターフェイスになっているので、実際のオブジェクトをクリックしながら順番をかえることもできます。

最適視点と可視化

次は、物を見るときに、どこらみるのがいいのという研究です。
例えば、心理学実験で、凹凸のあるかたちを提示して「どこからみたらいんでしょうね？」と質問をした実験結果があり、そこには法則が存在します。

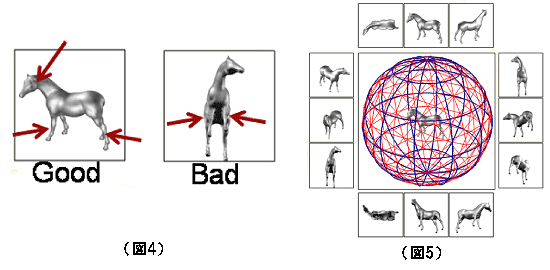
1つは特徴を重視する法則です。例えば馬は、顔や首や足など特徴部分見えないと馬と判らないですから、それが見える方向を最適な視点と考えます。
2つめは、視点位置が多少変化しても画像が変わらないという法則です。画面をチラチラっと揺らしたときに、劇的に画像が変わってしまう視点は最適と感じません。ぎりぎりで良く見えているのではなく、くるくるって廻したときに、しばらくの間「良いビュー」が続くような場所を良い視点と考えます。
3つめは、たくさんの情報（面）が見えていることです。
ビューエントロピーというものを計算し、その最大値を最適な視点とする考え方があります。
図5の中央は、馬を囲むすべての方向から見た場合に対して、エントリピーを計算し、その値を球面に色でマップしています。上が北半球、下が南半球で、赤いところがいい視点を意味します。
われわれは、これを、さきに紹介した特徴解析を使ってボリュームに拡張しました。
これについては検証のテストをしました。その結果、最適視点の位置は、完全に一致しないですが、その傾向は比較的きれいにシミュレートができ、そこそこ使えるという話になっています。

<<戻る

1

2

3

次へ>>

• 汎用可視化ソフトウェア
• 製品情報
• 事例
• 価格
• お役立ち情報
• サービス・サポート
• セミナー・イベント
• お問い合わせ
• サイトマップ