CAEを学ぶ
はじめての振動解析(3)減衰の基礎
はじめての振動解析(3)減衰の基礎 の概要

はじめての振動解析(1)(2)(3) 完全保存版 PDF を "無料" 公開中!

はじめての振動解析(1)(2)(3) 完全保存版 PDF サンプル
これさえ読めば振動解析の基本がわかる!
全3回のシリーズとなっております「はじめての振動解析」について、3回分の解析講座を1冊でお読みいただける完全保存版 PDF を公開いたしました。どなたでも簡単なフォーム入力のみでダウンロードいただけますので、是非この機会にご利用ください。
ページ数:30ページ
ファイル形式: PDF
はじめての振動解析(1)(2)(3) 完全保存版 PDF の目次
| (1) 振動の基礎とモーダル解析 1. はじめに 2. 振動のメカニズム 3. 振動解析の基礎 4. モーダル解析(固有値解析) 5. モーダル解析でできること 6. Ansys によるモーダル解析 7. Ansysモーダル解析事例 8. (補足) 実固有値解析と複素固有値解析 9. おわりに |
(2) 周波数応答解析モード重ね合わせ法の基礎 1. はじめに 2. 周波数応答解析 3. 周波数応答解析でできること 4. 周波数応答解析の解法:フル法(直接法) 5. 周波数応答解析の解法:モード重ね合わせ法 6. Ansysによる周波数応答解析 7. Ansys周波数応答解析事例 8. 付録 9. おわりに |
(3) 減衰の基礎 1. はじめに 2. 減衰の基礎 3. 減衰のタイプ 4. 粘性減衰 5. 構造減衰 6. モード減衰 7. 各種減衰の使い分け 8. 付録 9. おわりに |
1 はじめに
2 減衰の基礎
2.1 減衰は振動を抑える抵抗力
2.2 抵抗力は速度に比例
減衰は構造物に何らかの振動(動き)がないと働きませんので、減衰による抵抗力は速度に比例すると考えるのが簡単です。そこで減衰を速度に比例する粘性減衰として表現します。粘性減衰力![]() を(式1)で表し、比例定数
を(式1)で表し、比例定数![]() を(粘性)減衰係数と呼びます(図1)。
を(粘性)減衰係数と呼びます(図1)。

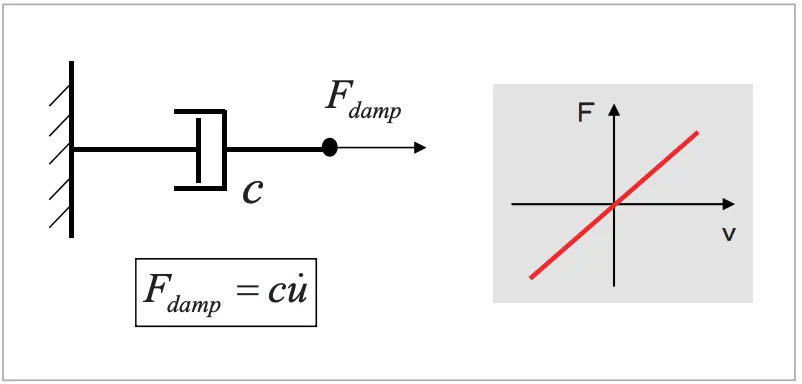
図1 粘性減衰
2.3 減衰するさまを臨界減衰比で評価
減衰![]() という物理量は、質量
という物理量は、質量![]() や剛性
や剛性![]() と違い非常にイメージしにくいです。そこで振動するかしないかの臨界減衰係数
と違い非常にイメージしにくいです。そこで振動するかしないかの臨界減衰係数![]() と減衰係数
と減衰係数![]() の比である臨界減衰比
の比である臨界減衰比![]() を算出して評価するのが一般的です。簡単な1 自由度粘性減衰系振動モデル(図2)で臨界減衰比を算出してみます。
を算出して評価するのが一般的です。簡単な1 自由度粘性減衰系振動モデル(図2)で臨界減衰比を算出してみます。
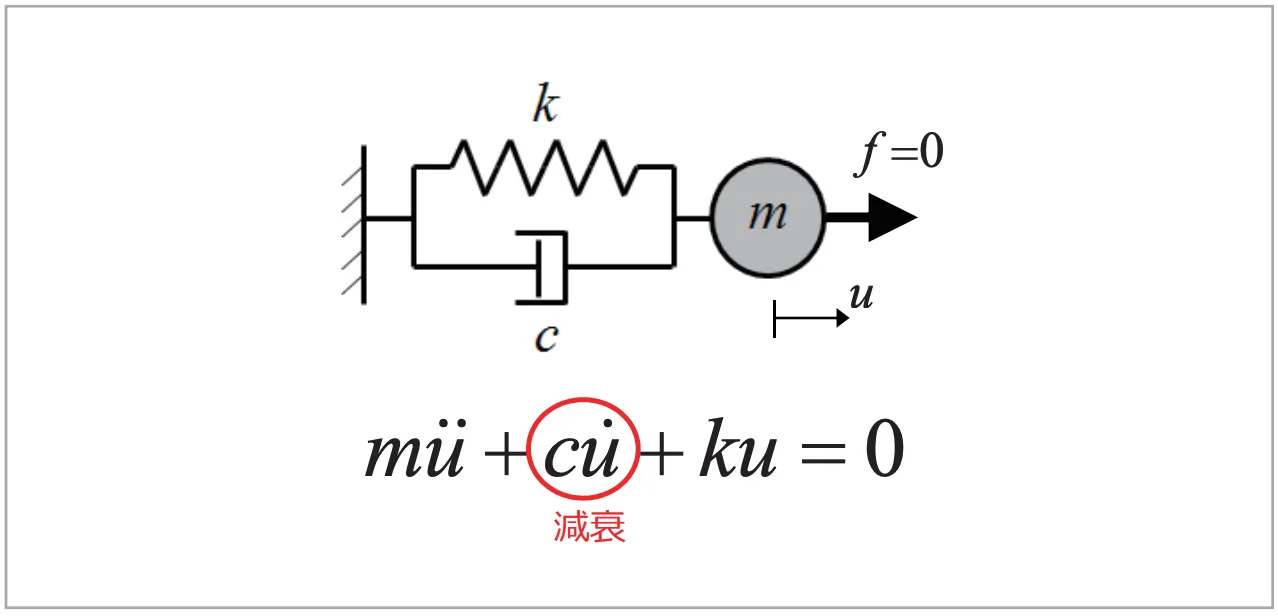
図2 1自由度粘性減衰系振動モデル
運動方程式は次式となります。
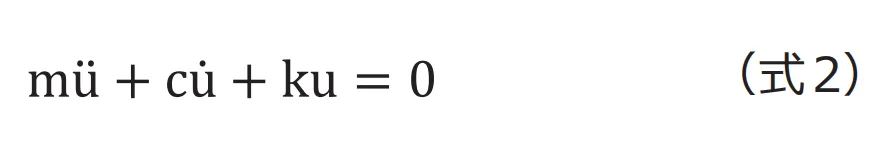
第1回のモーダル解析で行ったのと同じように、変位を![]() と仮定し代入します。
と仮定し代入します。
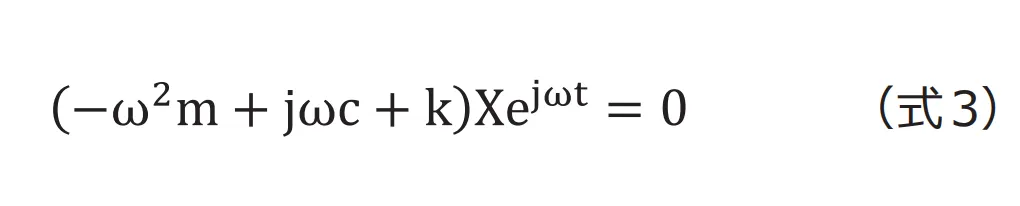
この式の解として![]() は単に振動しないことを意味するため除外すると次式となります。
は単に振動しないことを意味するため除外すると次式となります。
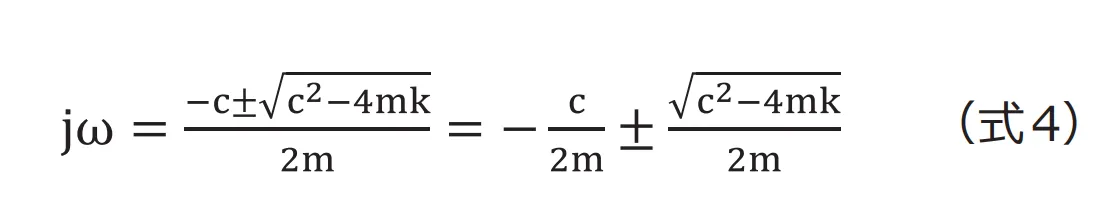
![]() の部分に着目すると、
の部分に着目すると、![]() が
が![]() より小さいか大きいかにより実数または虚数に分かれることがわかります。ここで
より小さいか大きいかにより実数または虚数に分かれることがわかります。ここで![]() 、固有振動数
、固有振動数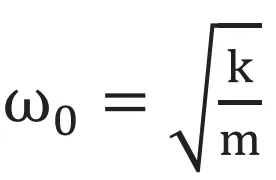 と定義すると次式になります。
と定義すると次式になります。
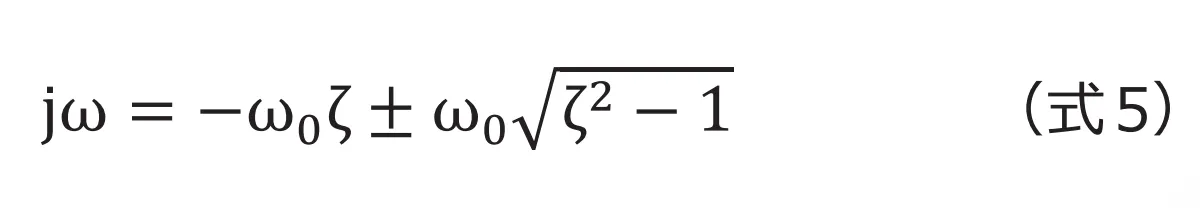
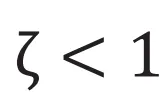 のとき
のとき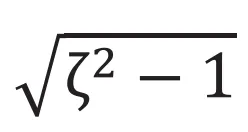 は複素数となります。ここで
は複素数となります。ここで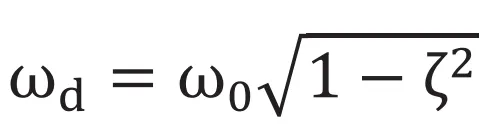 と定義すると
と定義すると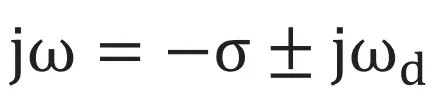 となり変位は(式6)で表現できます。
となり変位は(式6)で表現できます。 は振動状態を表し、
は振動状態を表し、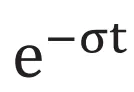 は時間が進むにつれ減衰する状態を表しますので減衰しつつ振動する結果となります。グラフで表すと(図3-b)です。
は時間が進むにつれ減衰する状態を表しますので減衰しつつ振動する結果となります。グラフで表すと(図3-b)です。
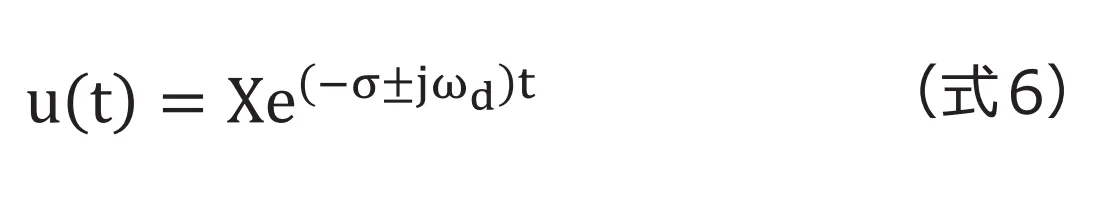
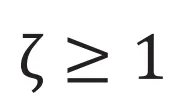 のとき
のとき
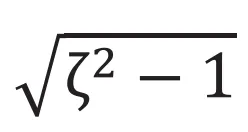 は実数となります。
は実数となります。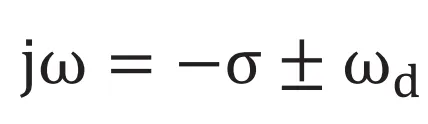 となり変位は(式7)で表現できます。今度は虚数成分がありませんので、時間が進むにつれ減衰する結果となります。グラフで表すと(図3-c)です。
となり変位は(式7)で表現できます。今度は虚数成分がありませんので、時間が進むにつれ減衰する結果となります。グラフで表すと(図3-c)です。
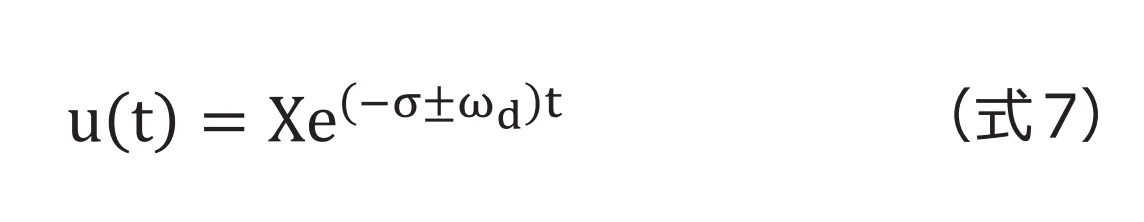
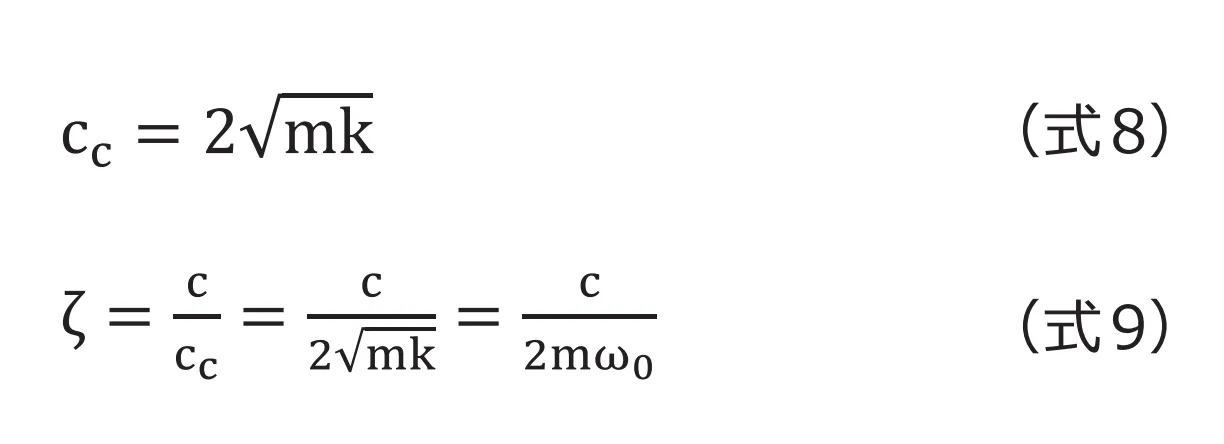
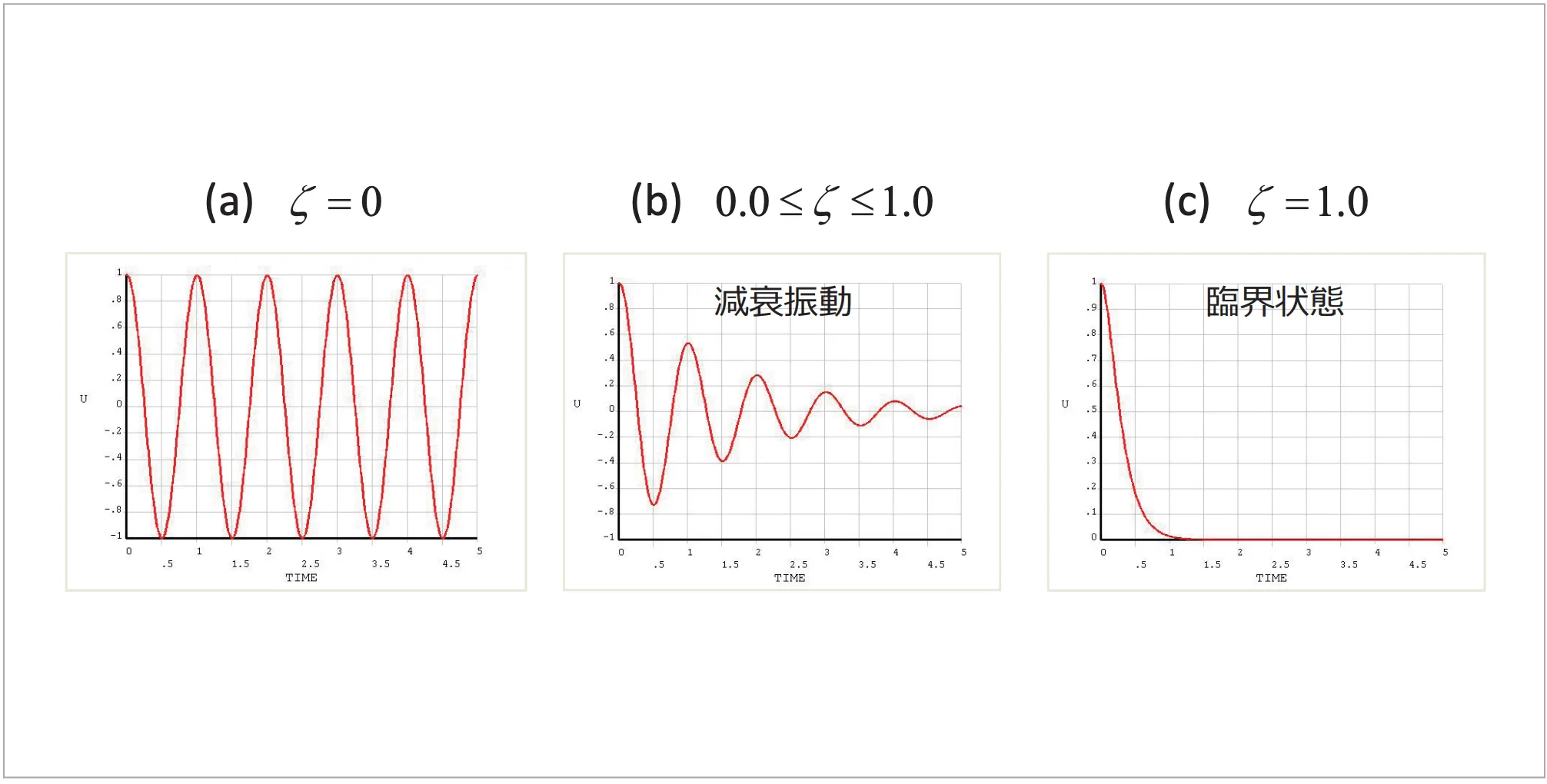
図3 臨界減衰比による振動の違い
2.4 対数減衰率
対数減衰率![]() は減衰自由振動の振幅比(
は減衰自由振動の振幅比(![]() )の自然対数をとったもので、臨界減衰比
)の自然対数をとったもので、臨界減衰比![]() と以下の関係式が成り立ちます(図4)。
と以下の関係式が成り立ちます(図4)。
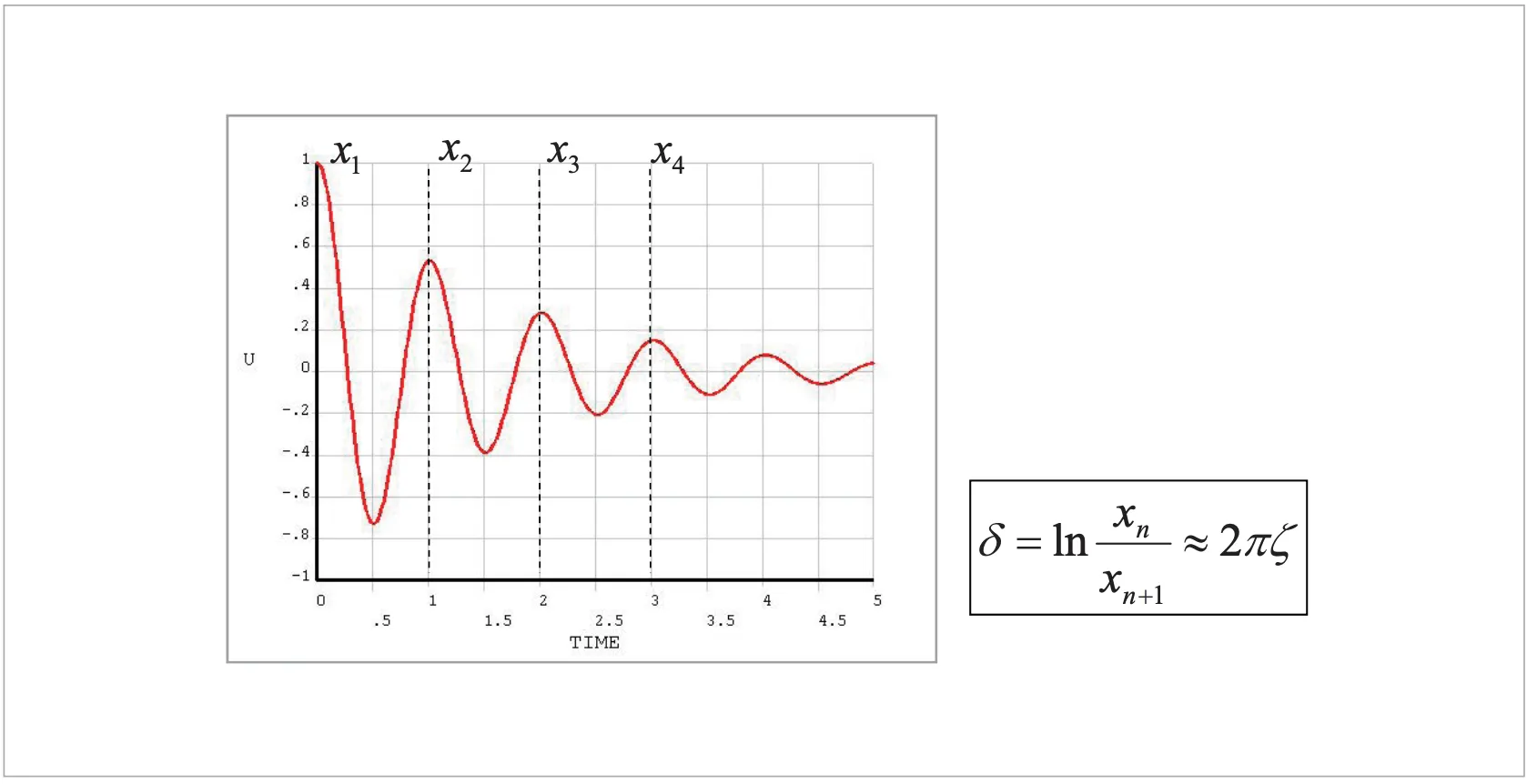
図4 対数減衰率
2.5 損失係数

2.6 エネルギーと臨界減衰比
系に減衰が存在すると振動時にエネルギーが消費されます。持っていたエネルギー![]() と1周期間に消費されるエネルギー
と1周期間に消費されるエネルギー![]() の比は以下の関係式が成り立ちます。
の比は以下の関係式が成り立ちます。

3 減衰のタイプ
すべてのメカニズムが解明されているわけではありませんが、減衰は以下の3つのタイプに分けることができます。
- 粘性減衰
空気抵抗や構造内部の摩擦抵抗などによって生じる減衰力で速度に比例します。
Ansysではレイリー減衰などで表現します。 - 構造減衰(履歴減衰、複素減衰とも呼ばれる)
構造内部に発生する減衰力でひずみ速度にほとんど依存しません。材料固有の減衰特性を持ちます。
Ansysでは一定構造減衰などで表現します。 - クーロン減衰
固体接触面に生じる摩擦による減衰力です(本稿では紙面の都合上取り扱いません)。
4 粘性減衰
4.1 要素粘性減衰
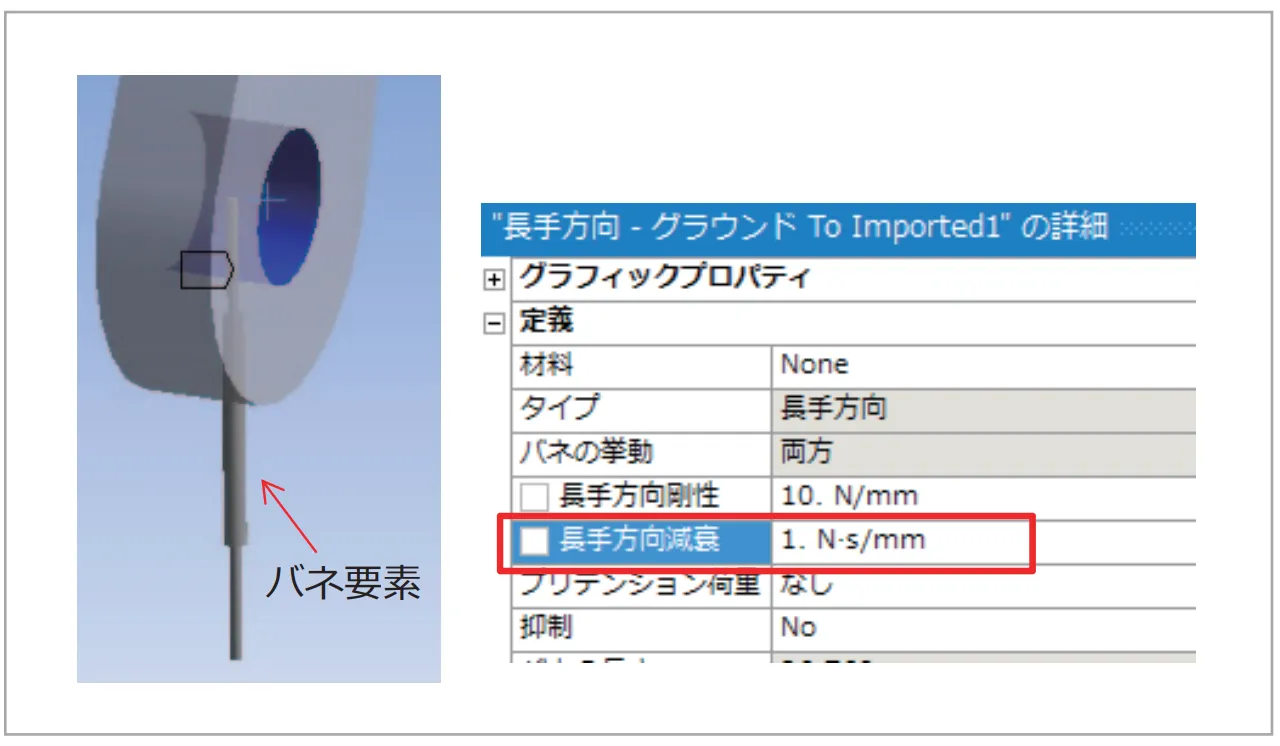
図5 要素粘性減衰
4.2 α 減衰
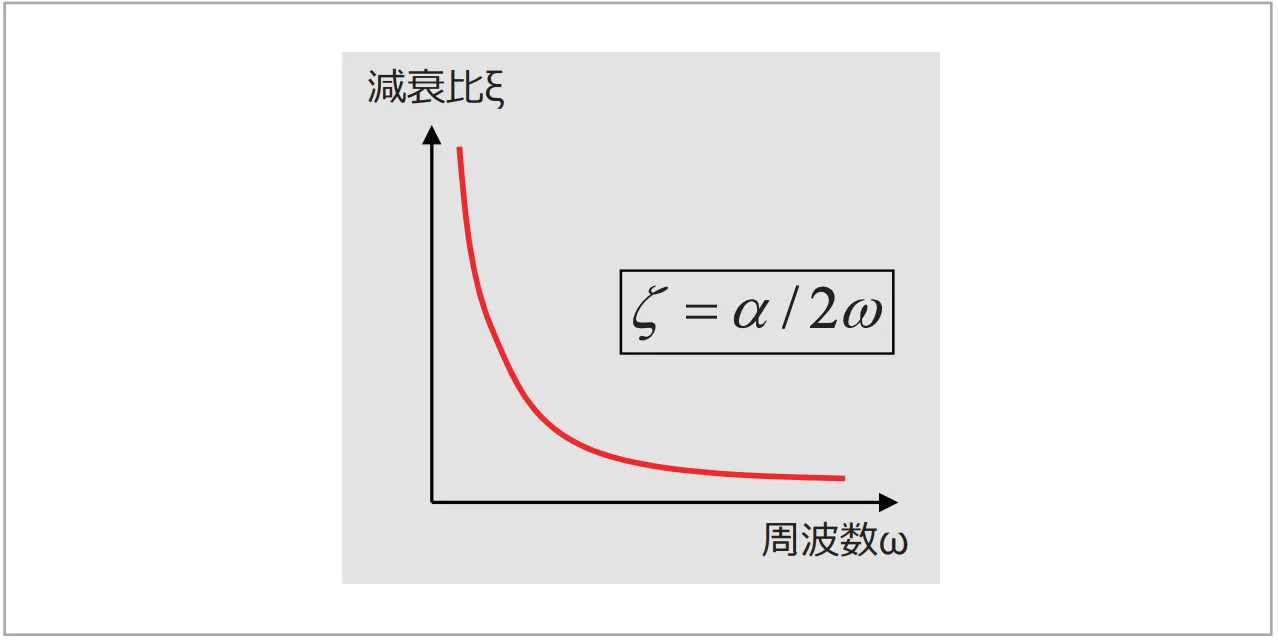
図6 α減衰
4.3 β減衰
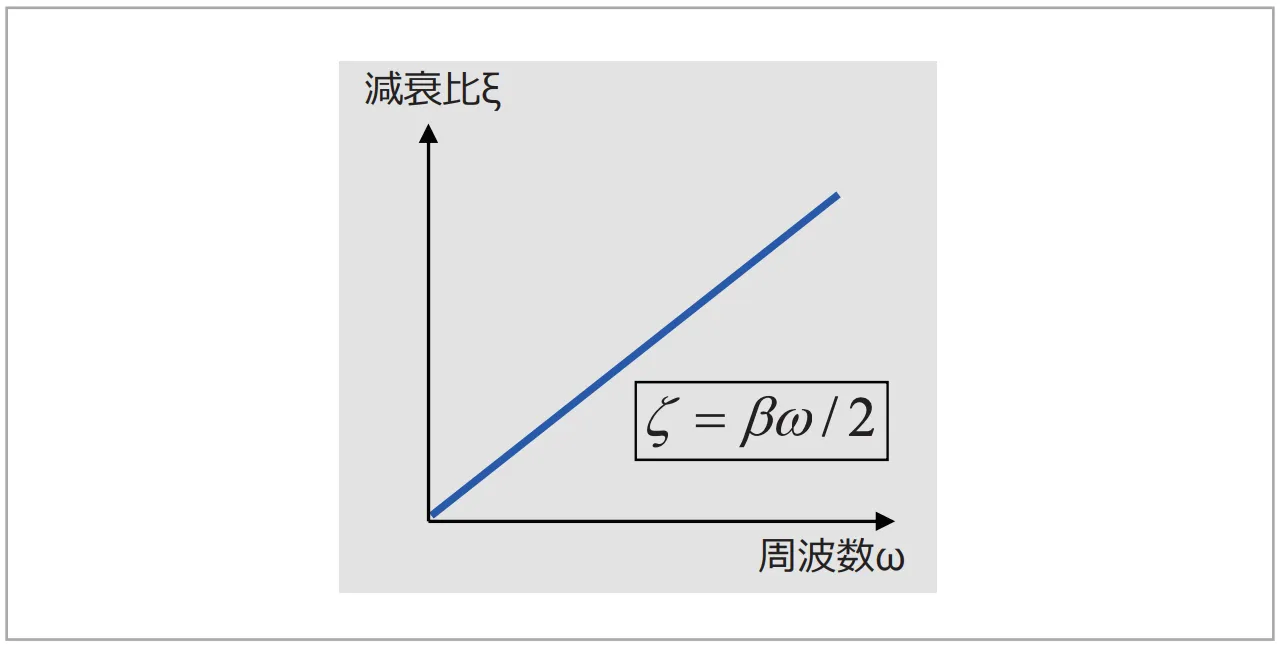
図7 β減衰
4.4 レイリー減衰
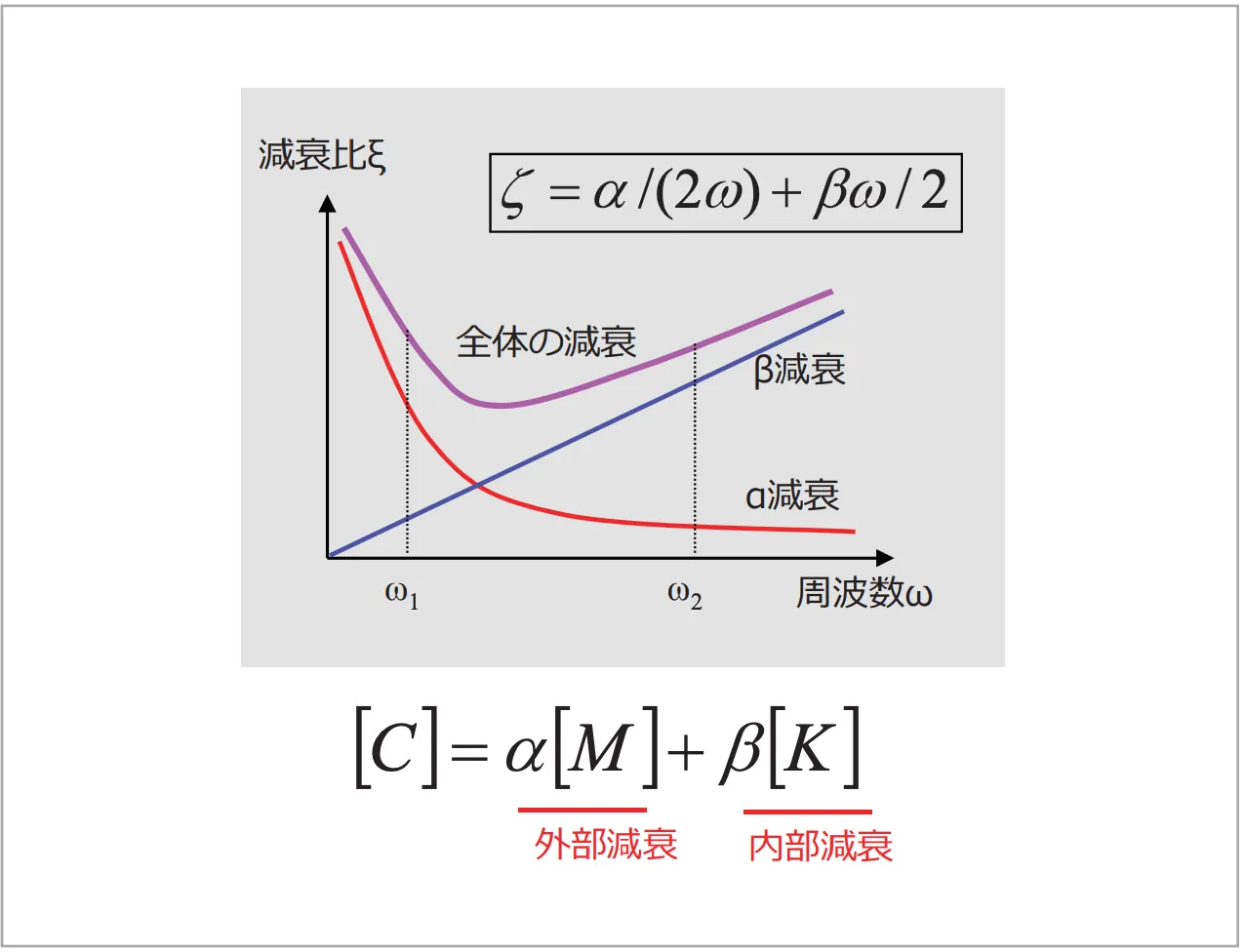
図8 レイリー減衰
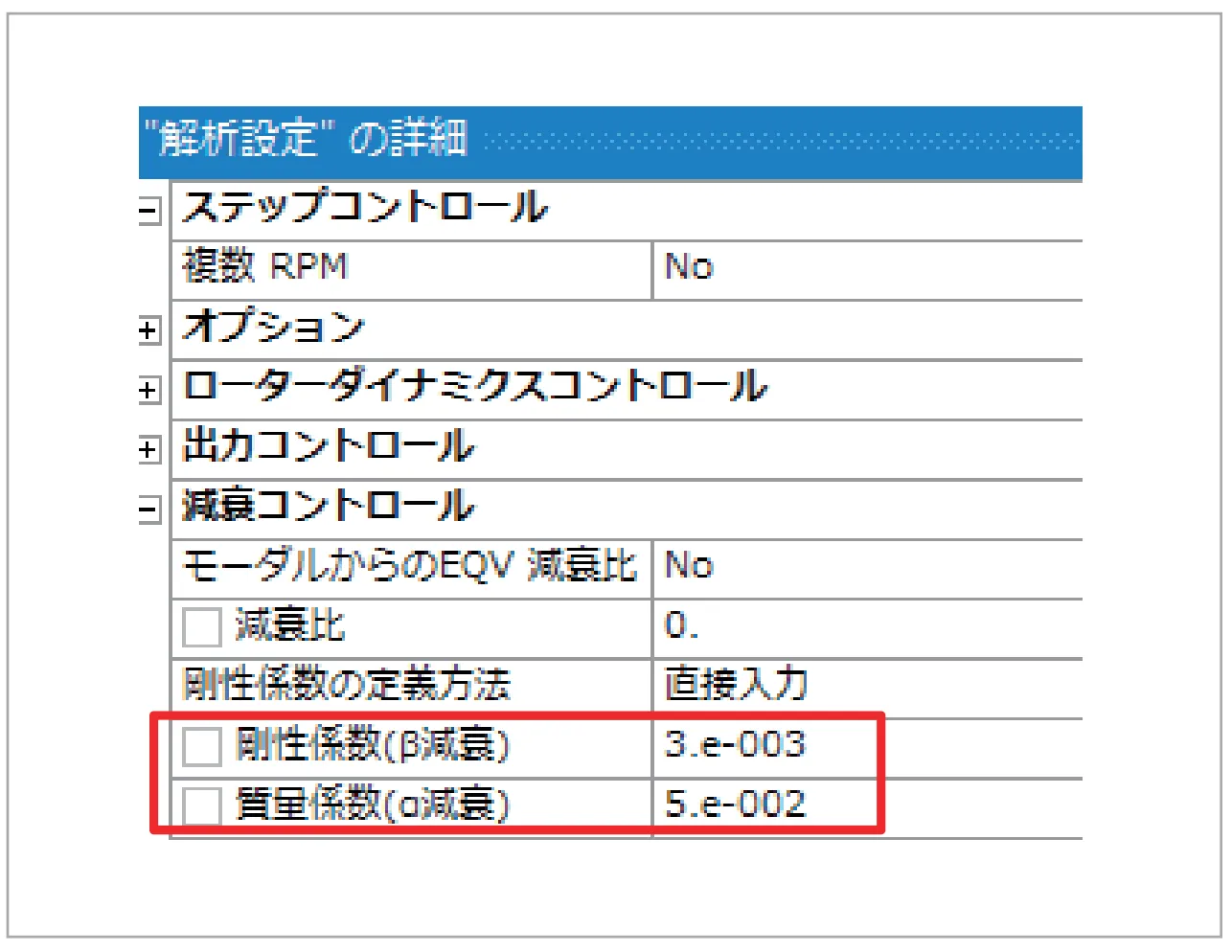
図9 レイリー減衰の設定
5 構造減衰
構造減衰は履歴減衰、複素減衰とも呼ばれ、速度に関係なく減衰比![]() が一定です。減衰として取扱いやすいのが特徴で、周波数応答解析でよく利用されます。計算上は周波数依存性を持つ等価粘性減衰で表現されます。
が一定です。減衰として取扱いやすいのが特徴で、周波数応答解析でよく利用されます。計算上は周波数依存性を持つ等価粘性減衰で表現されます。
5.1 等価粘性減衰係数
等価粘性減衰係数は、粘性減衰力が1 周期でなす仕事量が消費エネルギー![]() に変換され描くループ面積と同等であることを利用して求められます(図10)(式12)。
に変換され描くループ面積と同等であることを利用して求められます(図10)(式12)。
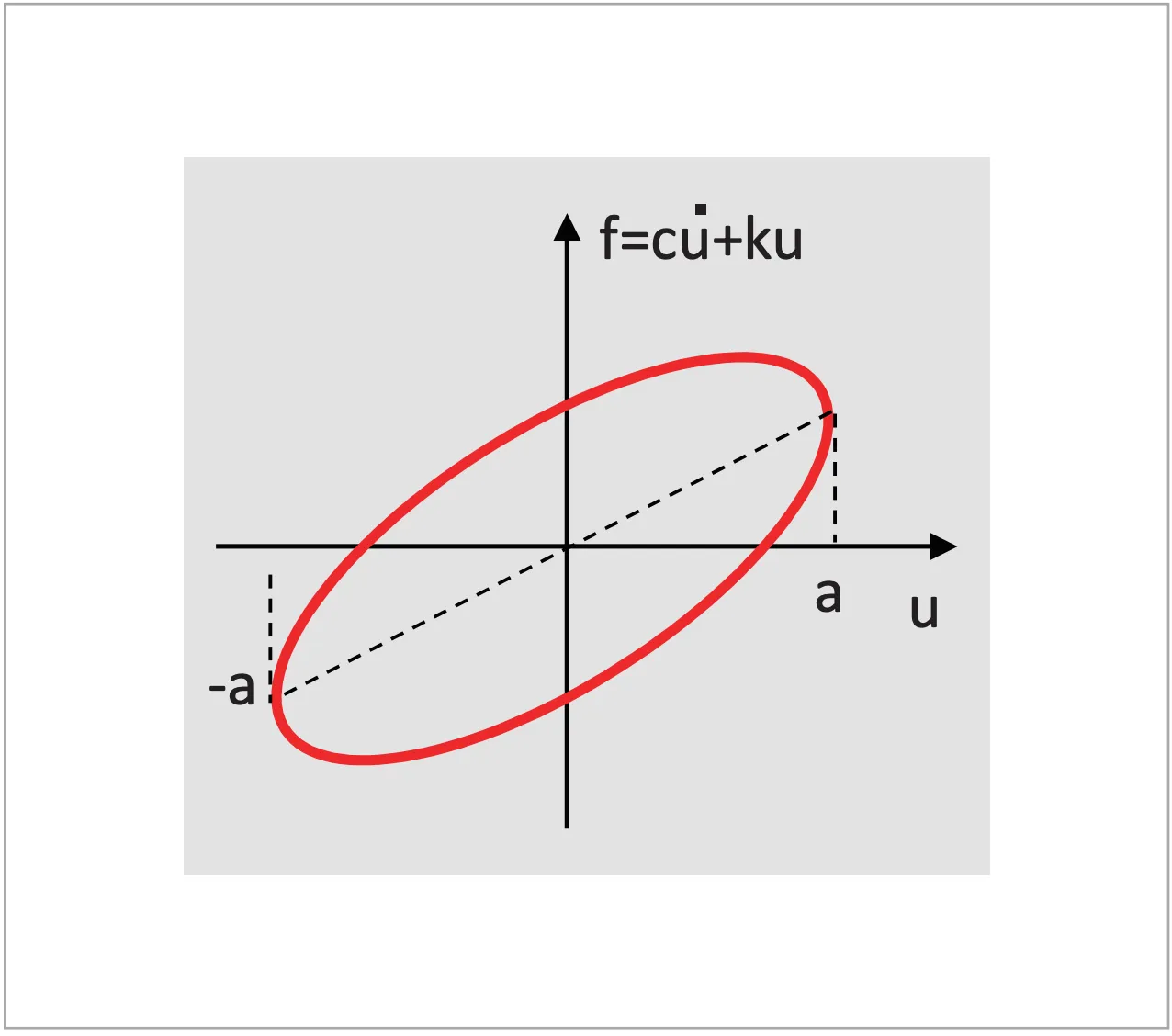
図10 強制振動時の履歴曲線
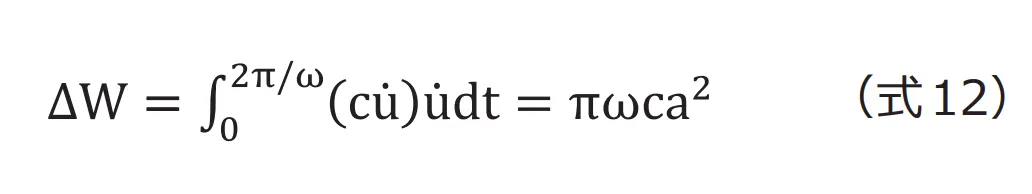
また、最大変位![]() に達したときに蓄えられるひずみエネルギー
に達したときに蓄えられるひずみエネルギー![]() は次式で求められます。
は次式で求められます。

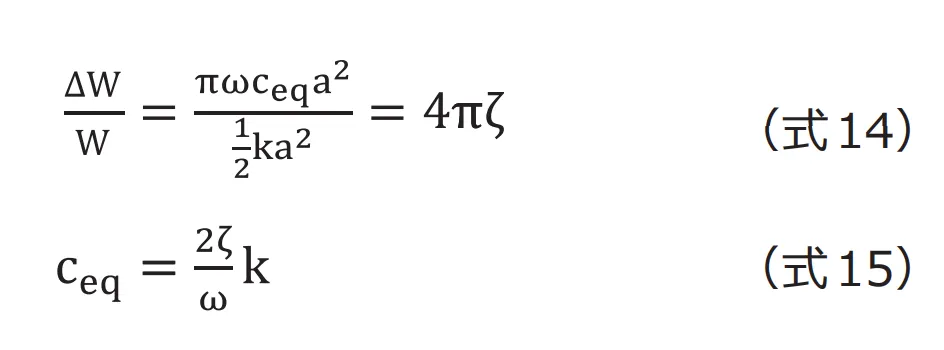
5.2 調和加振における運動方程式
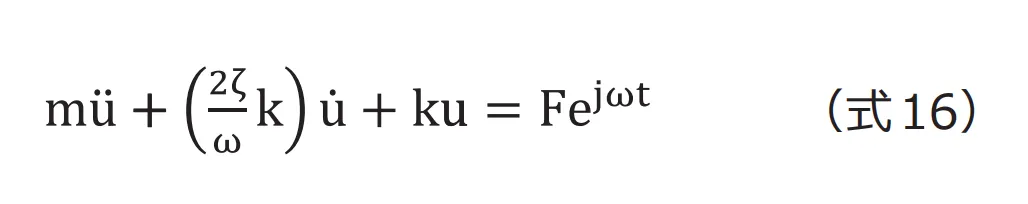
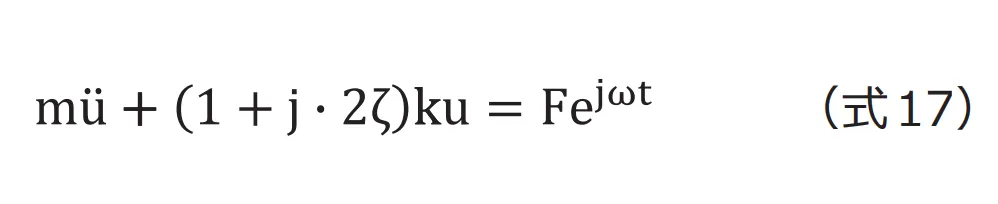
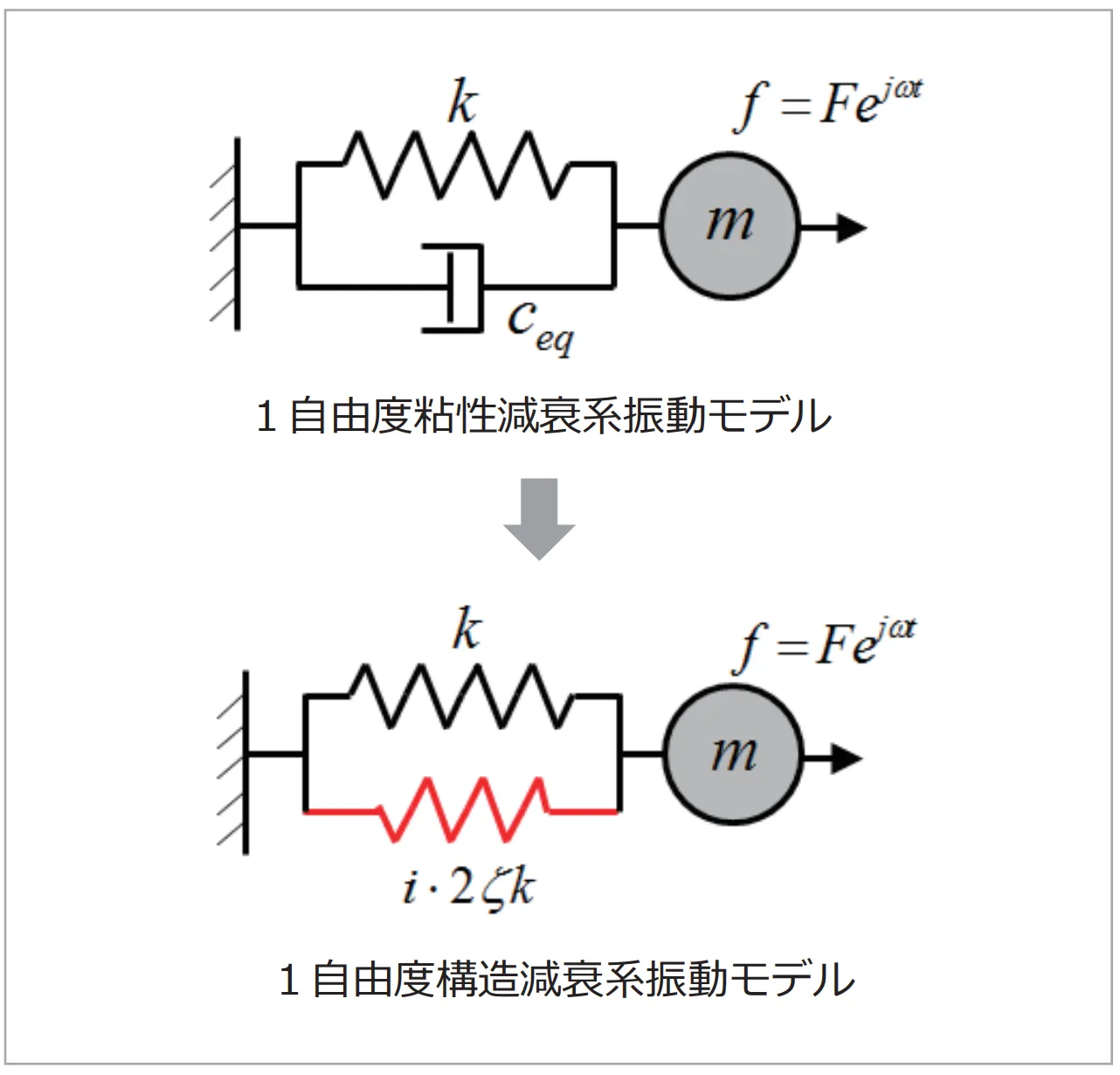
図11 1自由度構造減衰系振動モデル
5.3 一定構造減衰
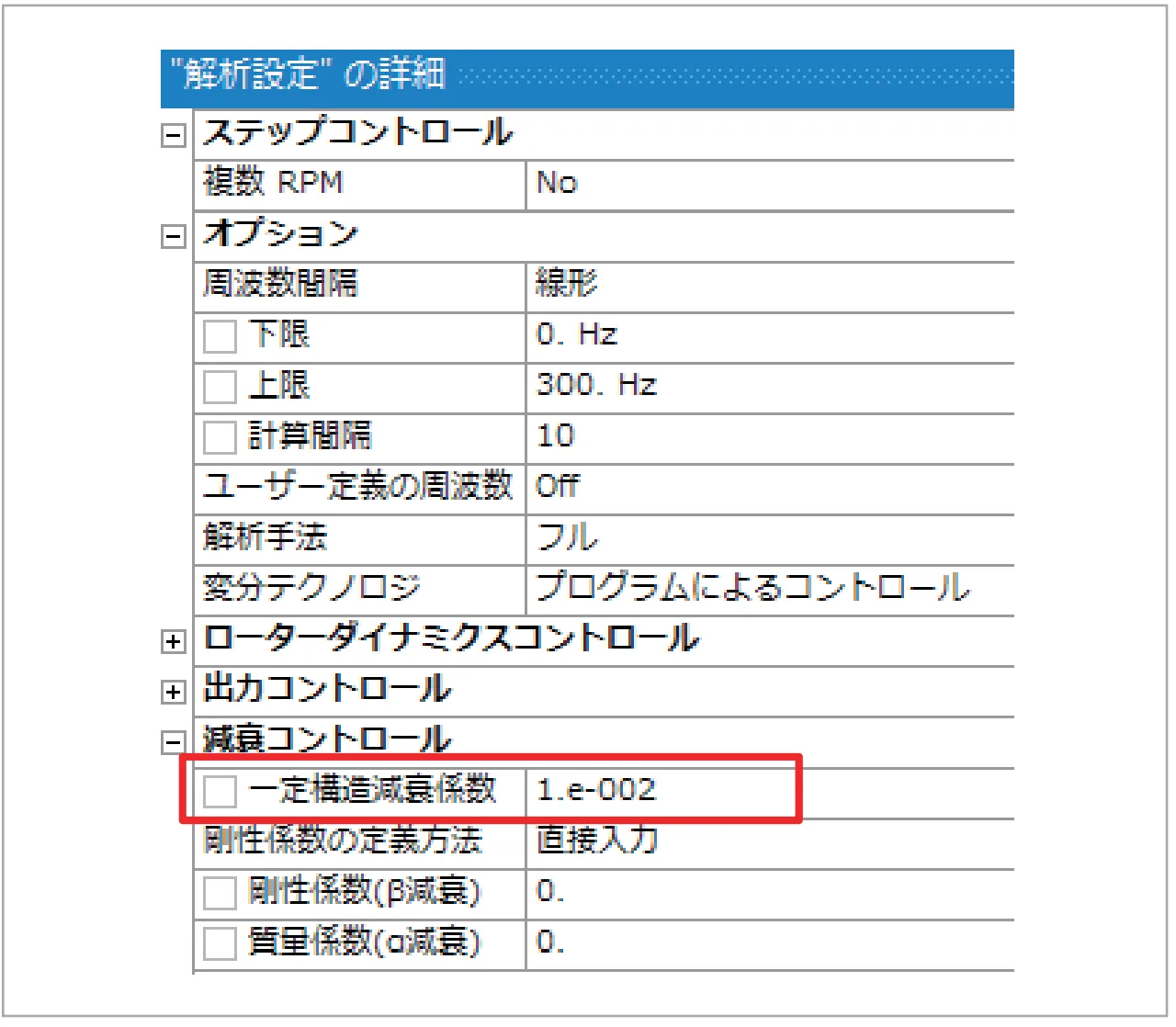
図12 一定構造減衰係数の設定
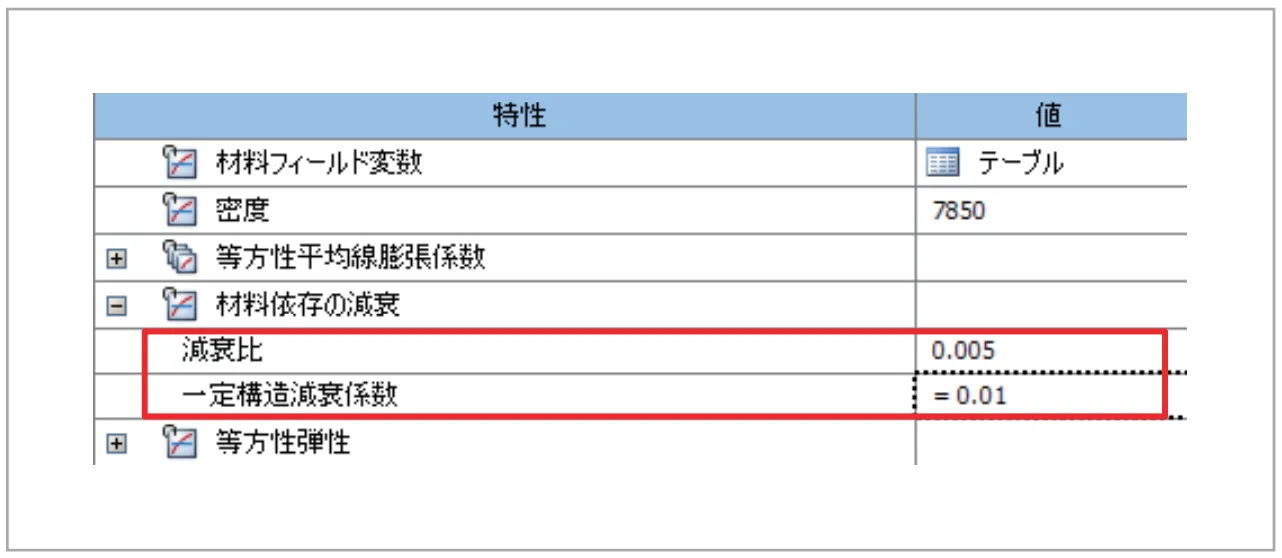
図13 材料別の一定構造減衰係数の設定
6 モード減衰
モード重ね合わせ法では、減衰マトリクス[C]を作成する代わりに、モードごとの臨界減衰比であるモード減衰比を設定します(図14)。モード減衰比は速度に依存しない減衰で、構造減衰とよく似ています。
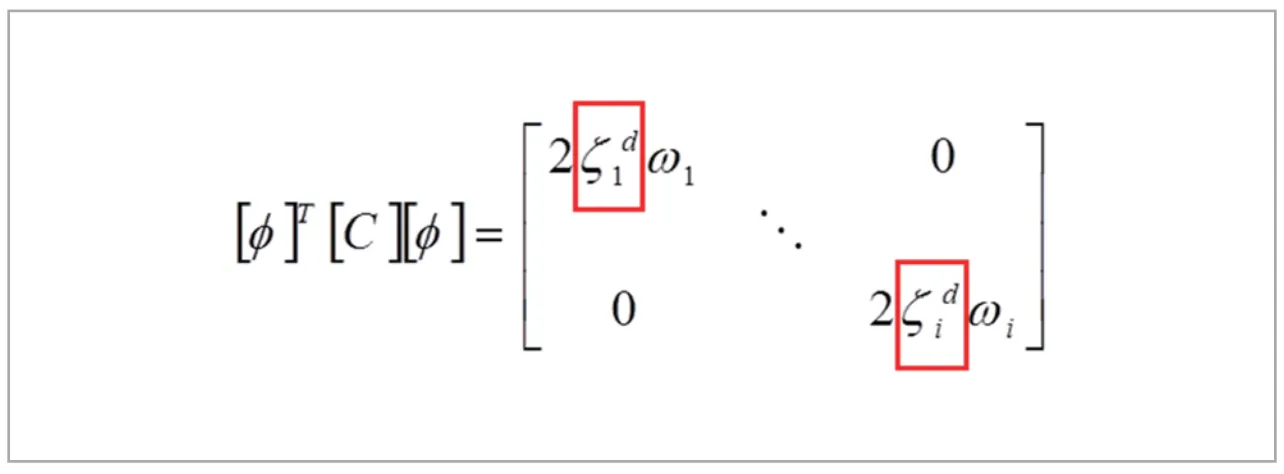
図14 モード減衰比
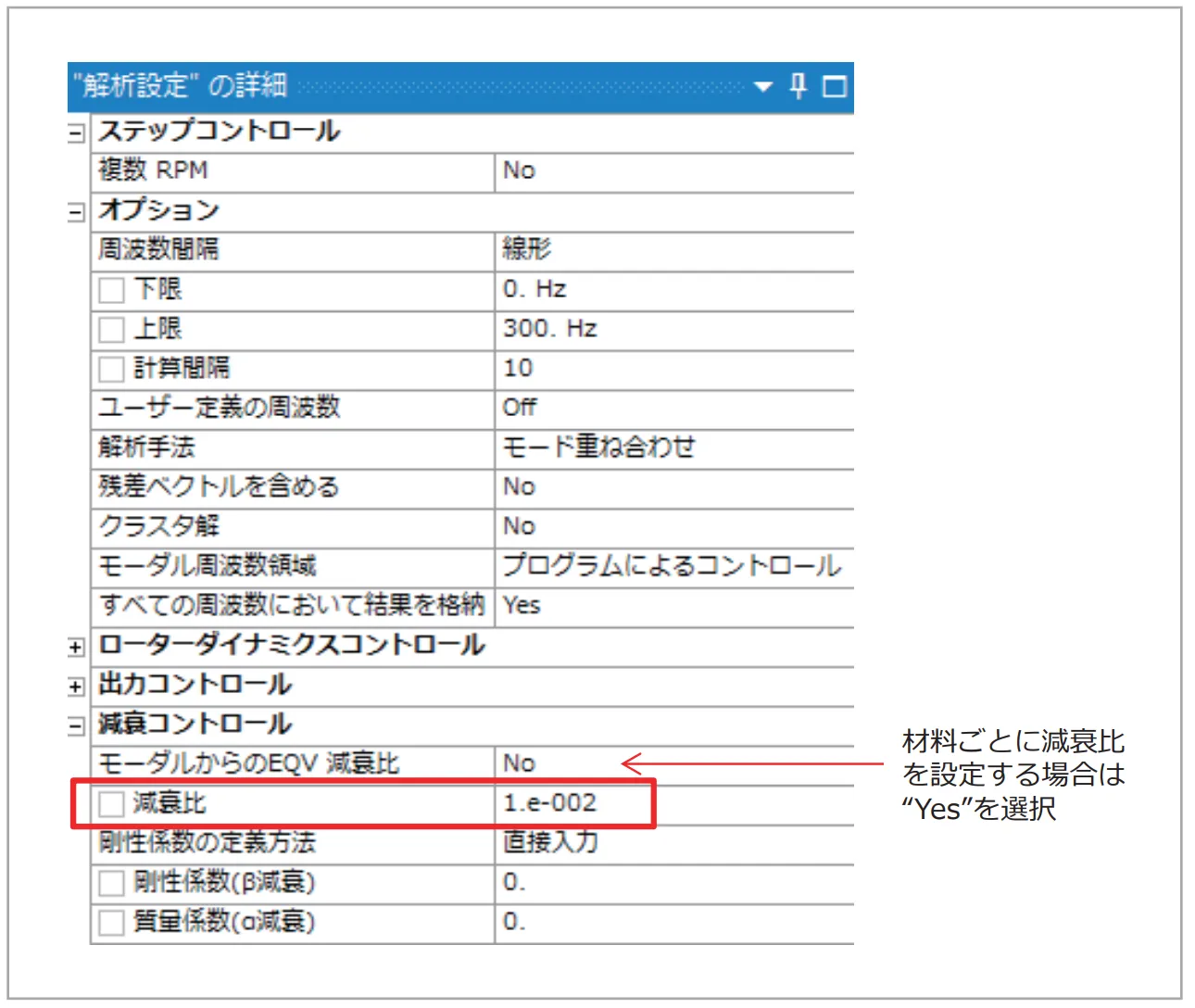
図15 モード減衰比の設定
7 各種減衰の使い分け
7.1 目的による使い分け
- とりあえず何らかの減衰が入ればよい場合
一定構造減衰(モード重ね合わせ法では一定のモード減衰比)を設定するのが簡単です。減衰はゼロにしないことを推奨します。ほぼ減衰が無いと想定される場合は、小さな値(0.001 など)を設定してください。 - 各部品や材料の減衰を個別に設定したい場合
フル法の場合:材料ごとに臨界減衰比を設定するのが簡単です。(図13)を参照してください。
モード重ね合わせ法の場合:(図15)の[モーダルからのEQV減衰比]をYesに設定してください。 - 実験モーダル結果からモードごとの減衰が見積もれる場合
MDAMPコマンドを利用して、モードごとに減衰を設定することができます。詳細はAnsysのコマンドリファレンスをご覧ください。 - 材料の周波数ごとの減衰データをお持ちの場合
これは主に粘弾性材料が該当すると思われます。粘弾性材料では周波数ごとの減衰比を定義するのが簡単です。詳細は弊社サポートへお問合せください。
7.2 解析タイプによる使い分け
- フル法周波数応答解析の場合
構造減衰がよく利用されますが、粘性減衰も使用できます。両者をともに使用すると効果が累積されます。
粘弾性材料はフル法周波数応答解析のみ対応します。 - モード重ね合わせ法周波数応答解析の場合
モード減衰がよく利用されますが、レイリー減衰も使用できます。両者をともに使用すると効果が累積されます。
要素減衰は使用できません(QR減衰法に変えることで対応可)。
8 補足
なお本稿でご紹介したAnsysのGUIはAnsys 2019 R2をもとに記載しております。バージョンにより多少異なる場合がありますので、ご注意ください。
9 おわりに
全3 回にわたって振動解析の基礎をご紹介してまいりましたが、振動解析は非常に奥深い世界で、本シリーズで触れていない機能やテクニックが数多く存在します。弊社では豊富な知見をベースにセミナーや受託解析、コンサルティングなどのサービスを提供しております。もし振動解析でお困りの点がございましたら、弊社営業部にお問い合わせください。
参考文献
[ 1] Ansysオンラインヘルプ > 構造解析ガイド > 構造解析の概要 > 減衰
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-
剥離・接合強度評価ソリューション ~Ansys Workbench Mechanicalで実施できる剥離解析~
-

レーザー集光の高温レンズ歪みを克服するAnsys連携ソリューション
-
周波数応答解析×自動抽出で干渉チェックを高速化
-

直観的な操作で無線/デジタルフィルタの設計・最適化を支援する〜Ansys Nuhertz FilterSolutions〜
-
流体機器設計の新たな一歩
~Ansys Discoveryで加速する設計改革~
-
筐体の冷却性能を構想設計から見える化 (手戻りを削減できる)
~Ansys Discoveryで始める電気筐体製品の設計改革~
-
若手でもすぐに使えるリアルタイム解析 (勘と経験からの脱却)
~Ansys Discoveryによる30名規模メーカーの設計改革~
-
構想設計ですぐにリアルタイム検証 ~解析専任者ゼロでも使いこなせるAnsys Discovery~
~解析専任者ゼロでも使いこなせるAnsys Discovery~