CAEを学ぶ
はじめての振動解析(2) 周波数応答解析・モード重ね合わせ法の基礎
はじめての振動解析(2) 周波数応答解析・モード重ね合わせ法の基礎 の概要

はじめての振動解析(1)(2)(3) 完全保存版 PDF を無料公開中

はじめての振動解析(1)(2)(3) 完全保存版 PDF サンプル
全3回のシリーズとなっております「はじめての振動解析」について、3回分の解析講座を1冊でお読みいただける完全保存版 PDF を公開いたしました。どなたでも簡単なフォーム入力のみでダウンロードいただけますので、是非この機会にご利用ください。
ページ数:30ページ
ファイル形式: PDF
はじめての振動解析(1)(2)(3) 完全保存版 PDF の目次
| (1) 振動の基礎とモーダル解析 1. はじめに 2. 振動のメカニズム 3. 振動解析の基礎 4. モーダル解析(固有値解析) 5. モーダル解析でできること 6. Ansys によるモーダル解析 7. Ansysモーダル解析事例 8. (補足) 実固有値解析と複素固有値解析 9. おわりに |
(2) 周波数応答解析モード重ね合わせ法の基礎 1. はじめに 2. 周波数応答解析 3. 周波数応答解析でできること 4. 周波数応答解析の解法:フル法(直接法) 5. 周波数応答解析の解法:モード重ね合わせ法 6. Ansysによる周波数応答解析 7. Ansys周波数応答解析事例 8. 付録 9. おわりに |
(3) 減衰の基礎 1. はじめに 2. 減衰の基礎 3. 減衰のタイプ 4. 粘性減衰 5. 構造減衰 6. モード減衰 7. 各種減衰の使い分け 8. 付録 9. おわりに |
1 はじめに
本シリーズ第1回では振動の基礎とモーダル解析(固有値解析)について取り上げました。モーダル解析では固有振動数と固有モードを求めることができましたが、加振力は考慮しない解析手法でした。本稿(第2回)で取り上げる「周波数応答解析」は、加振力を考慮した振動応答を求めるのによく使われる手法です。
この「モーダル解析」と「周波数応答解析」が振動解析の双璧をなす解析手法です。たとえば一般社団法人 日本機械学会が主催する計算力学技術者資格認定事業[1]の振動分野2級の認定試験では、モーダル解析・周波数応答解析、そして時刻歴応答解析が出題範囲とされていることからも重要性を感じていただけると思います。
本稿では周波数応答解析と、効率よく計算する手法である「モード重ね合わせ法」の基礎を合わせてご説明いたします。
2 周波数応答解析
2.1 周波数応答解析とは?
周波数応答解析は単純な正弦波の荷重(加振力)が負荷されたときの構造物の定常的な応答を評価する解析です。
モーダル解析に比べると解く式が複雑になるため計算時間がかかりますが、後ほどご紹介する「モード重ね合わせ法」により効率よく計算することもできます。
2.2 定常振動を構成する3つの要素
先ほど「定常的な応答を評価する」と書きましたが、定常的な振動とはどのようなものなのかを最初に確認しておきます。定常的な振動は振幅・周波数・位相の3つの要素から成り立っています(図1)。
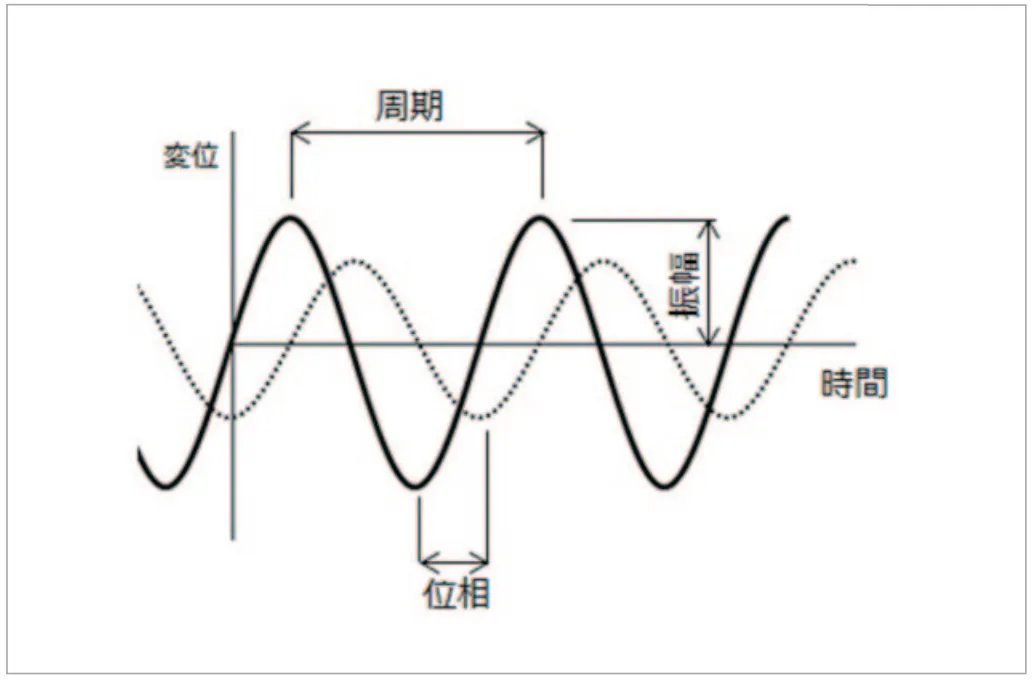
図1 定常振動を構成する3要素
- 振幅:振動の大きさ(最大値)のことです。
- 周波数:1 秒間に何周期の振動があるかを表します。
- 位相:振動するタイミングのずれを表します。
要するに構造物の変位が正弦波のように周期的に振れている状態が「定常的な応答」です(正弦波と異なり位相はゼロとは限りません)。周波数応答解析を実施すると、構造物の振幅・周波数・位相を調べることができます。
周波数応答解析では定常振動状態を仮定していますので、定常でない振動状態、たとえばランダムな加振力が加わる状態や、応答が定常的にならない状態などは解析できません。
2.3 モーダル解析と周波数応答解析の違い
前回(第1 回)で取り上げたモーダル解析と周波数応答解析の主な違いは以下のとおりです。
- 加振力を負荷したときの振動応答を評価できる
モーダル解析では固有振動数が求められますが、これはあくまで「共振しそうな周波数」がわかるだけで、実際に共振したときにどのような応答になるかは不明で した。一方、周波数応答解析は振動応答を求めることができますので、より現実に即した結果が得られます。 - 振幅に物理的な意味がある
モーダル解析で出力される変位は比率だけに意味がありましたが、周波数応答解析で求められる振幅は物理 的な意味があり絶対値として評価できます(変位だけでなく応力やひずみも物理的な意味があります)。 - 固有振動数以外の周波数における情報も取得できる
モーダル解析は固有振動数が求められ、それ以外の周波数における情報はありませんでした。一方、周波数応答解析では任意に指定した周波数の情報を取得できます。
2.4 1自由度系の非減衰強制振動
続いて理論的な側面から周波数応答解析の理解を深めていきます。まずは簡単な1 自由度モデル(図2)で強制振動を理論的に求めてみます。
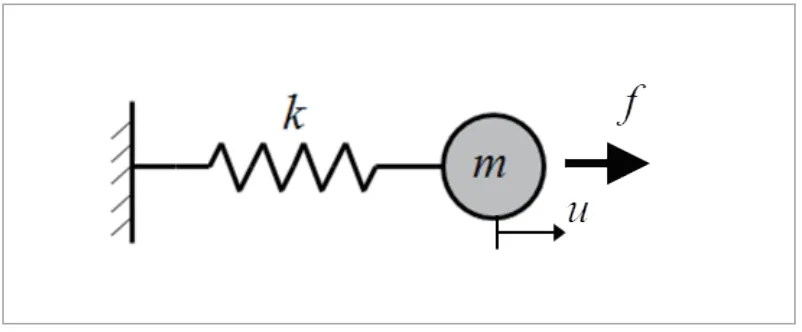
図2 1自由度非減衰強制振動
このモデルで非減衰強制振動の条件は、加振力![]() および減衰
および減衰![]() となります(複素指数関数を使用した理由については付録をご参照ください)。
となります(複素指数関数を使用した理由については付録をご参照ください)。
強制振動状態の運動方程式は(式1)のようになります。
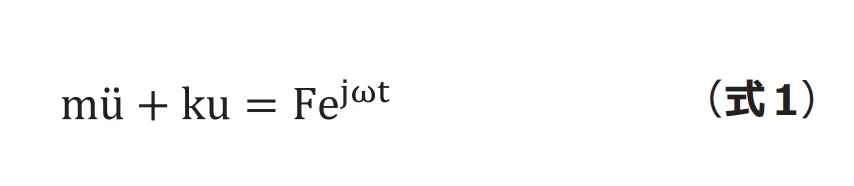
周波数応答解析は定常振動を前提としていますので、 モーダル解析のときと同様に変位![]() と定常振動 状態を仮定します。
と定常振動 状態を仮定します。![]() は複素数、
は複素数、![]() は角振動数です。代入すると振幅
は角振動数です。代入すると振幅![]() は(式3)のようになります。
は(式3)のようになります。
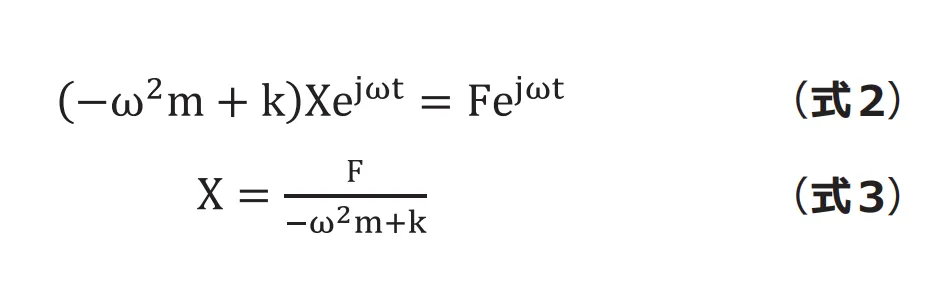
もし(式3)![]() でが固有振動数と等しい、つまり
でが固有振動数と等しい、つまり![]() となった場合、分母がゼロとなり振幅は無限大に発散します。このように加振力の周波数と系の固有振動数が一致して非常に大きな振幅が発生することを共振と呼びます。
となった場合、分母がゼロとなり振幅は無限大に発散します。このように加振力の周波数と系の固有振動数が一致して非常に大きな振幅が発生することを共振と呼びます。
2.5 1自由度系の減衰強制振動
もし振幅が無限大に発散してしまうと構造物はことごと く壊れてしまうことになりますが、現実の世界では何らか の減衰が働いて振幅が抑えられます。そこで(図3)のよう に減衰を考慮した強制振動を求めてみます。運動方程式は (式4)のようになります。
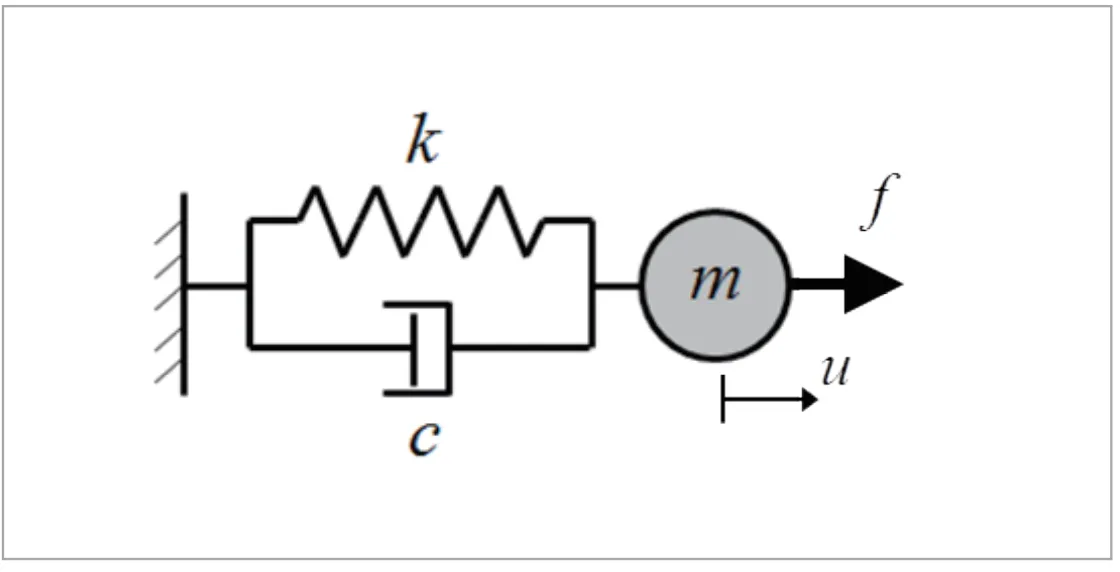
図3 1自由度粘性減衰系強制振動
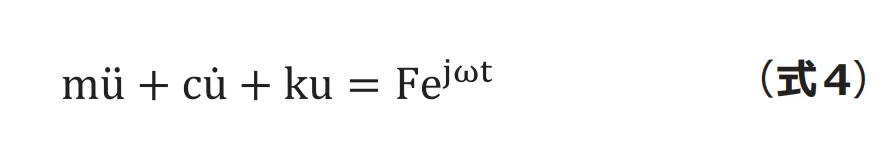
先ほどと同様の方法で計算していきます。
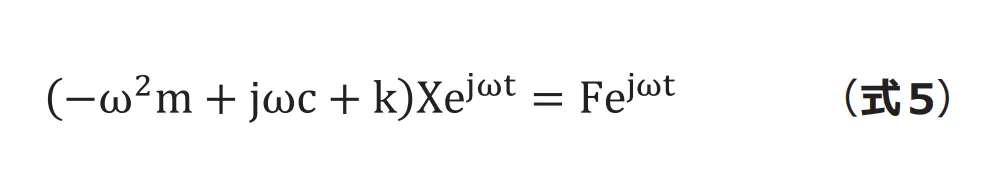
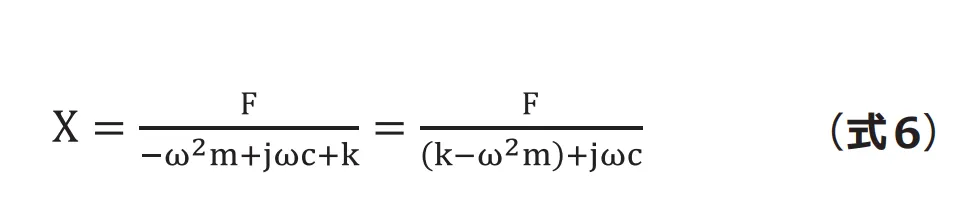
ここで、無減衰1 自由度系の固有振動数![]() を用いて
を用いて![]() を定義し、
を定義し、![]() とおきます(減衰を
とおきます(減衰を![]() このようにおく理由は次回第3 回で説明します)。さらに、静解析における変位を
このようにおく理由は次回第3 回で説明します)。さらに、静解析における変位を![]() (式6)に代入してみます。
(式6)に代入してみます。
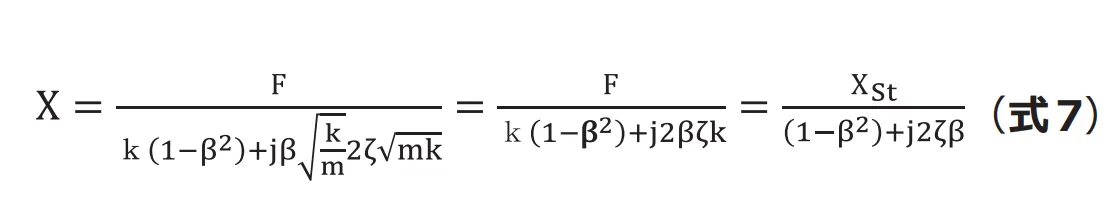
分母に虚数![]() が入っているとわかりづらいので、複素指数関数で表現します。複素指数関数の関係(式8, 9, 10) を用いて整理すると(式11)となります(複素指数関数について詳しくは付録を参照してください)。
が入っているとわかりづらいので、複素指数関数で表現します。複素指数関数の関係(式8, 9, 10) を用いて整理すると(式11)となります(複素指数関数について詳しくは付録を参照してください)。
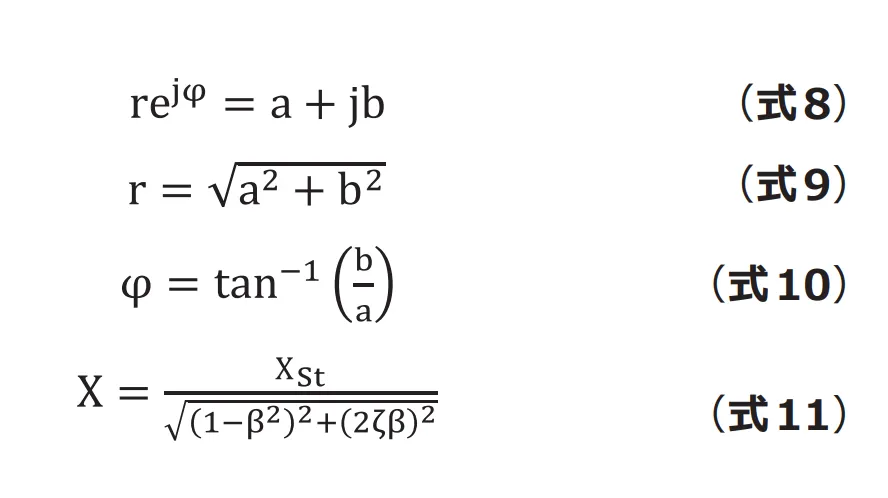
よって、変位解は(式12)となります。
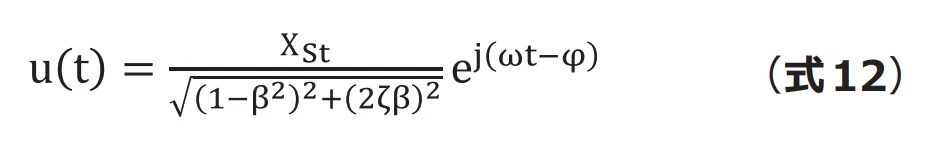
ここで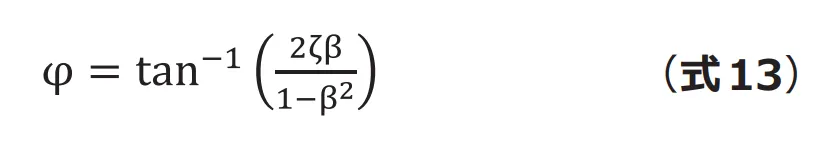
応答倍率が最大になるのは![]() すなわち、
すなわち、 ![]() となるときです。固有振動数より若干低くなりますが、
となるときです。固有振動数より若干低くなりますが、![]() は通常小さな値なので、実用上は固有振動数で共振する(応答倍率が最大になる)と考えて構いません。このときの最大振幅は(式14)となり、振幅は物理的な意味を持つ値となります。
は通常小さな値なので、実用上は固有振動数で共振する(応答倍率が最大になる)と考えて構いません。このときの最大振幅は(式14)となり、振幅は物理的な意味を持つ値となります。
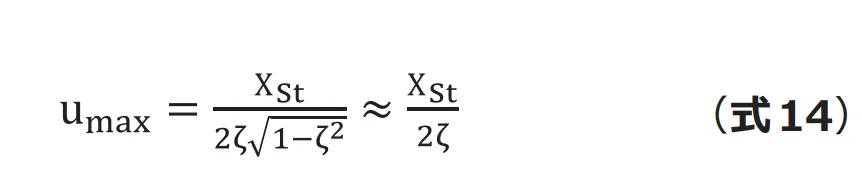
横軸に周波数をとって応答倍率![]() と
と![]() 、位相
、位相![]() と
と![]() との関係をプロットすると(図4)のようになります。周波数応答解析を実施すると、このように周波数ごとの振幅や位相を評価できます。
との関係をプロットすると(図4)のようになります。周波数応答解析を実施すると、このように周波数ごとの振幅や位相を評価できます。
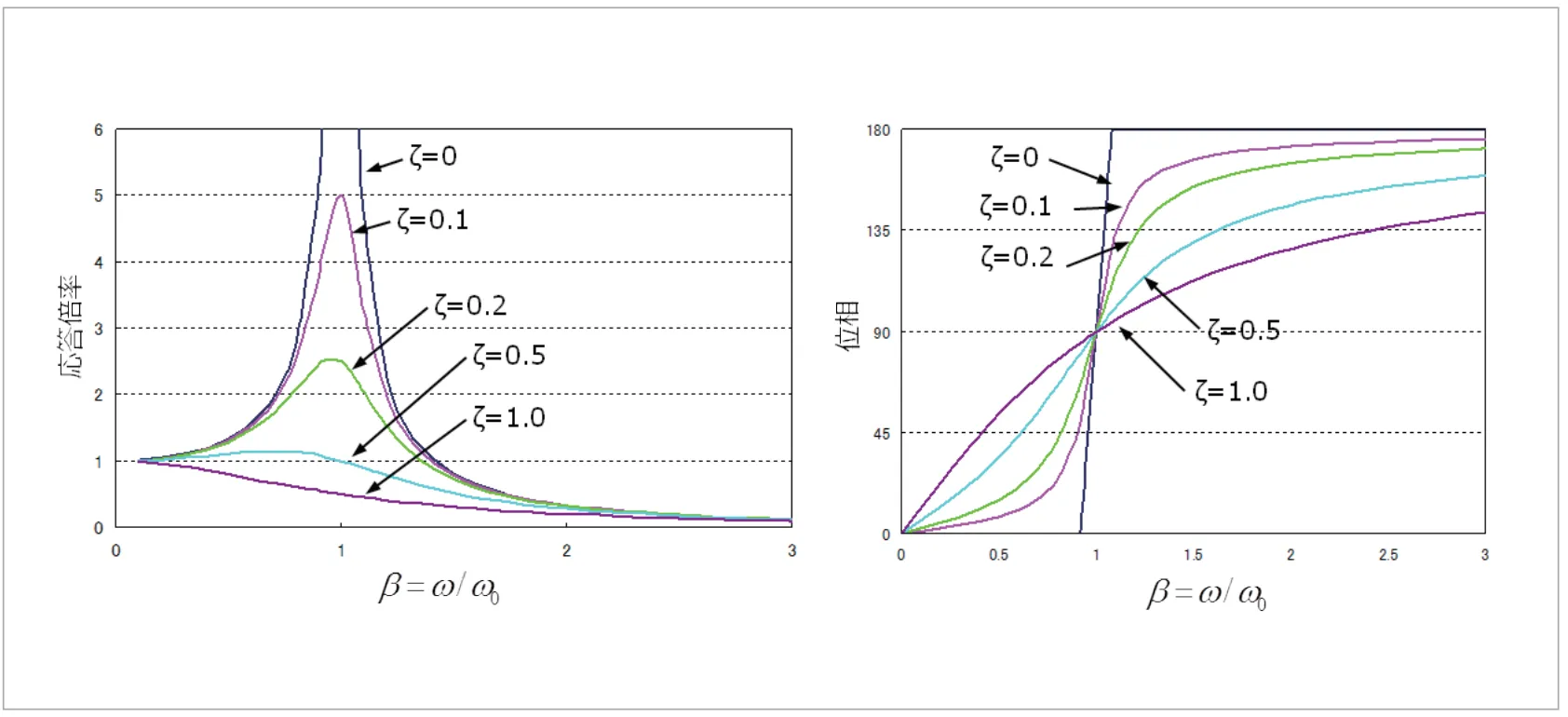
図4 応答倍率とβ、位相とβの関係
2.6 周波数応答解析の注意点
前述のとおり周波数応答解析では物理的に意味のある振幅を求めることができます。ただし、このことはCAEの解 析結果が実物と同じ振幅になることは意味しません。先の (式14)で示したとおり振幅は減衰次第で変わりますので、 実物と同じような振幅を得られるようにするには適切な減 衰を設定したり、(アセンブリでは)部品間の結合のモデル化を工夫するなど様々なテクニックが必要です。
3 周波数応答解析でできること
周波数応答解析でできることは大きく分けて3つあります。
- 共振時の構造物の応答を評価
共振時に構造物の振幅がどのぐらいになるのか、そして発生する応力はどのぐらいなのかを評価できます(図5)。 - 振動対策後の効果を確認
何らかの振動対策を行ったときの効果を確認できます。主な振動対策としては、加振力そのものの低減や、剛性や質量を変えて固有振動数を変化させる、制振材や防振材を追加するといった方法があります(図6, 7)。 - 周波数毎で構造物の動特性を評価
周波数分析することで構造全体の振動挙動を把握しやすくなります。
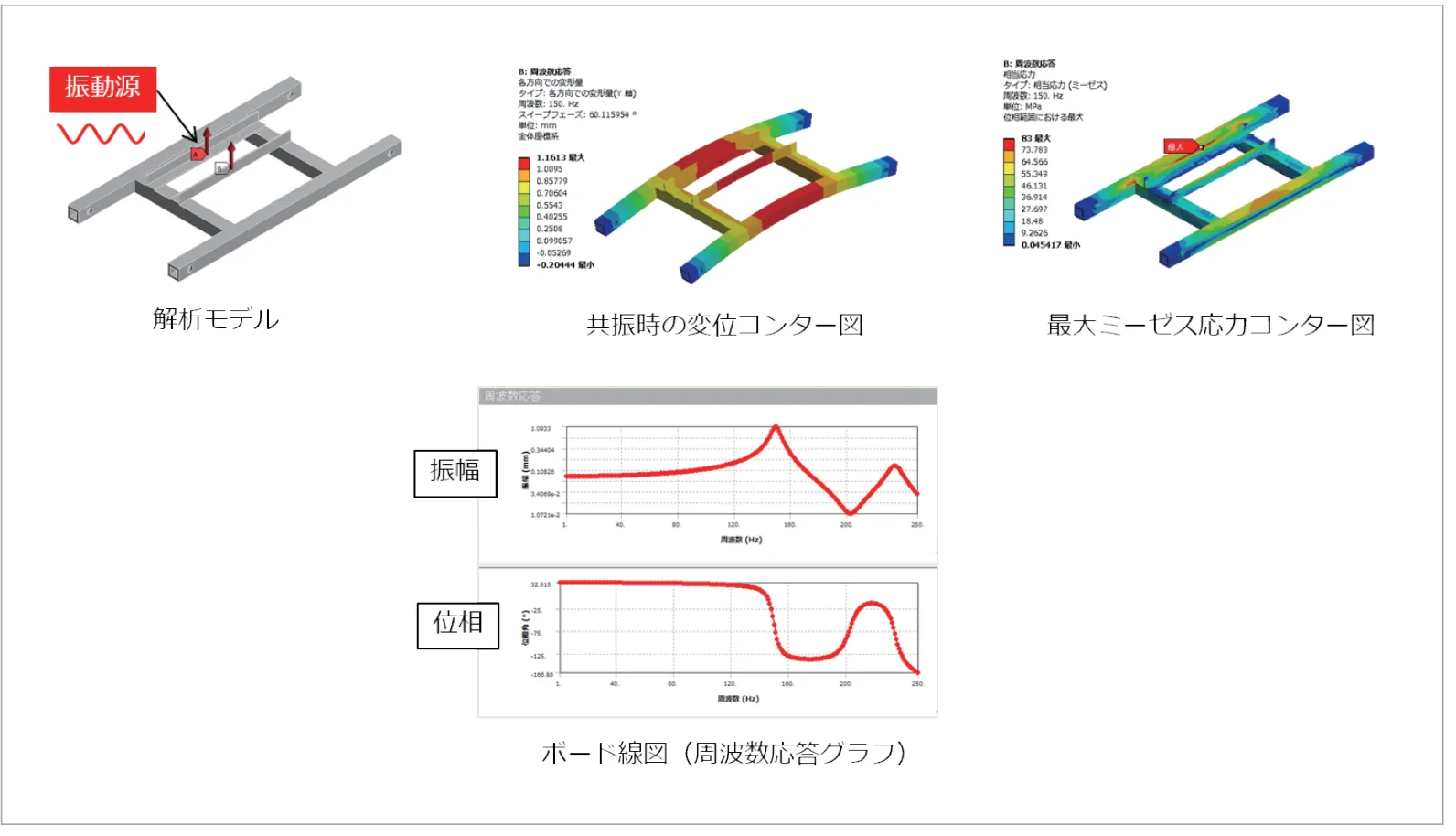
図5 共振時の構造物の応答評価
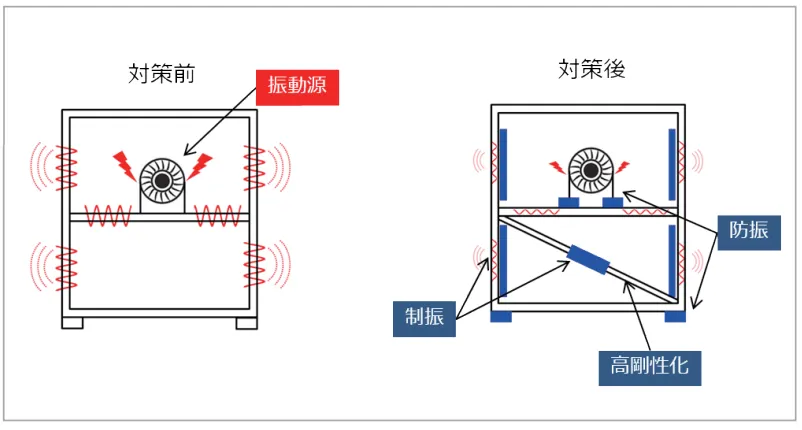
図6 振動対策例
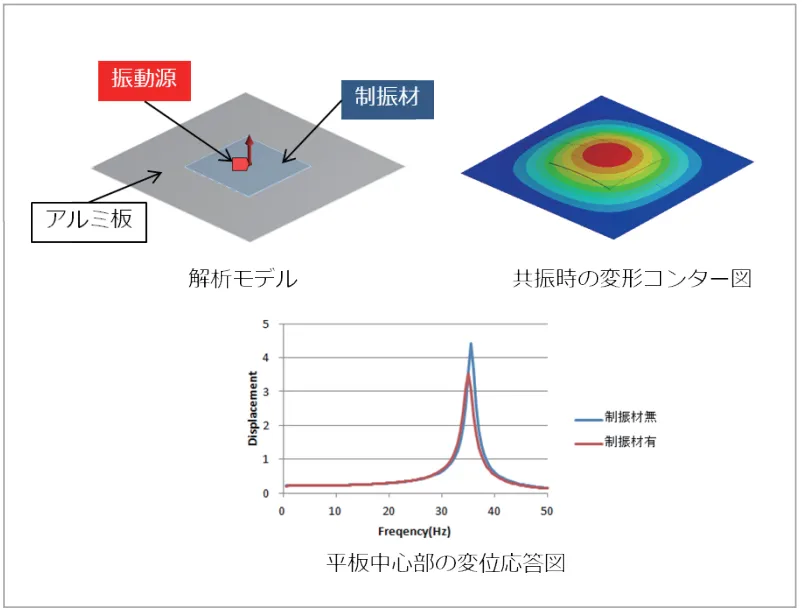
図7 アルミ板上面に制振材を貼付した効果を確認
4 周波数応答解析の解法: フル法(直接法)
周波数応答解析には大きく分けてフル法(直接法)とモー ド重ね合わせ法があります。フル法は周波数応答の式をそ のまま計算する手法です。
4.1 多自由度系のフル法周波数応答解析
前述の1自由度減衰系の問題を多自由度系に拡張します。 まず運動方程式は(式15)のようになります。
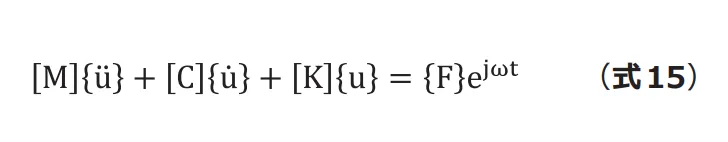
先ほどと同様に変位を仮定して計算すると、変位は (式16)のように求められます。
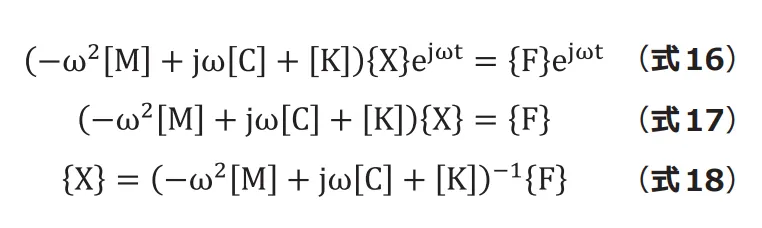
この式では逆行列の計算が必要なことがわかります。しかも逆行列の中にωが入っていますのでωが変わるたびに逆行列を計算する必要があります。たとえば100 個の周波数に対して応答を求めたい場合は、100 回逆行列を計算しなければならず、とても計算コストが高くなります。
(図8)のような横軸周波数で滑らかな周波数応答関数を描こうとした場合、計算コストが大きな壁になります。
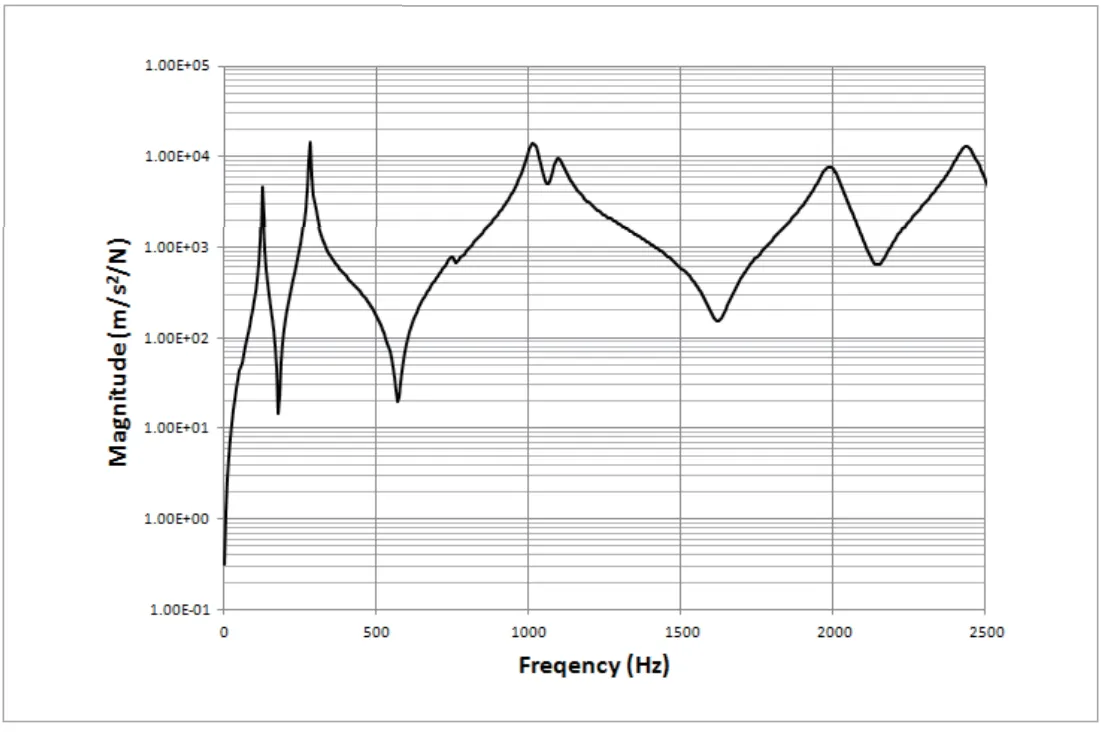
図8 周波数応答関数
5 周波数応答解析の解法: モード重ね合わせ法
フル法で解析すると計算コストが高くなるのが欠点でした。そこで計算を効率的に行えるモード重ね合わせ法 (Mode superposition method、略称MSUP)がよく使 われます。モード重ね合わせ法は「振動は固有モードが混 り合って生じている」として、モーダル解析で求めた固 有ベクトルを係数倍し足し合わせることで動的応答を得る 手法です(図9)。
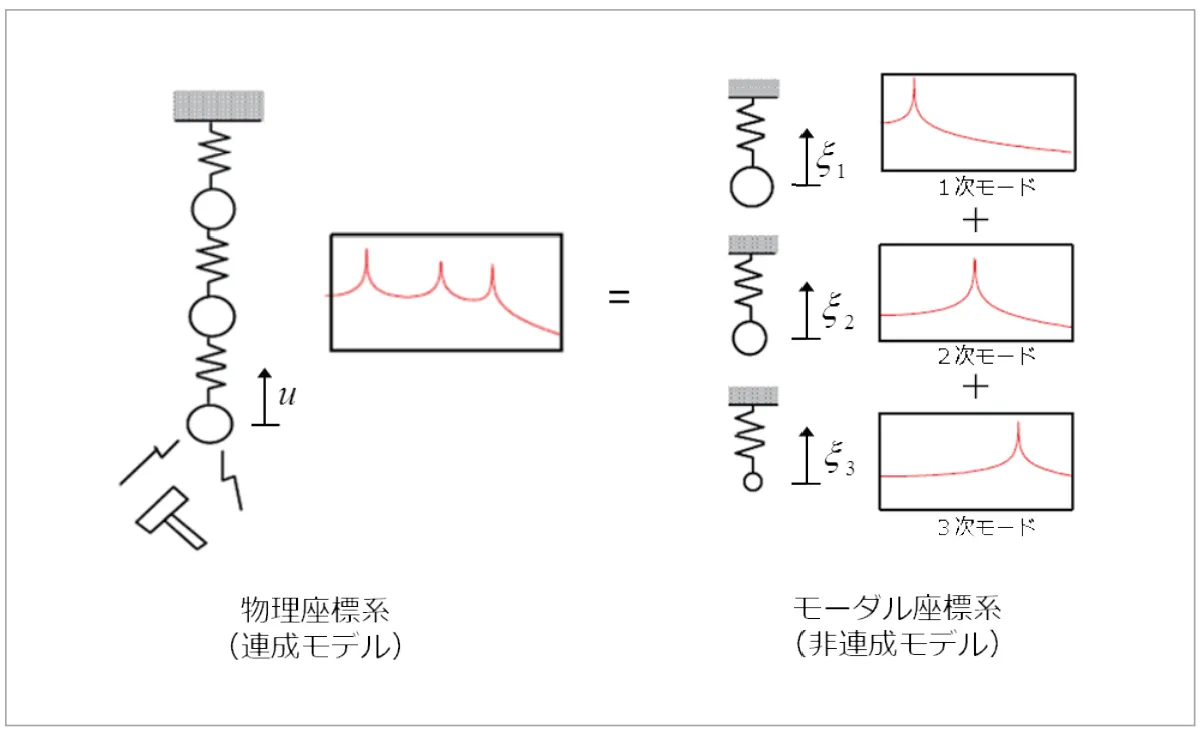
図9 モード重ね合わせ法の概念図
5.1 モード座標
まずはモード座標について解説します。2次元において (図10)で示すようにベクトルは、2 つの直交するベクトル![]() との線形和
との線形和![]() と
と![]() の(重ね合わせ)で表わすことができます。
の(重ね合わせ)で表わすことができます。
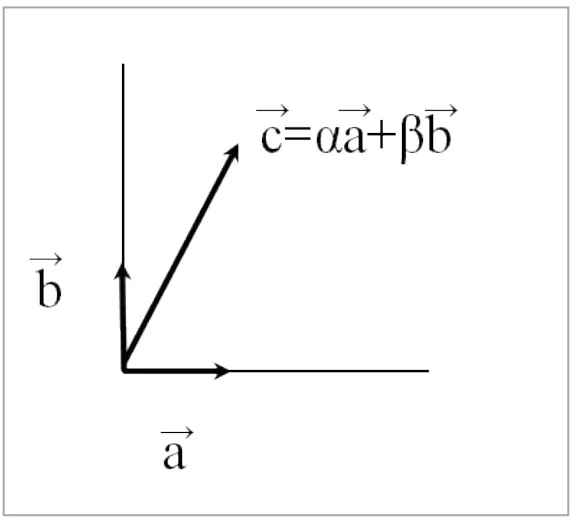
図10 直交ベクトルの線形和で表現
これをモードと変位の関係に応用します。第1 回で登場した固有ベクトルは、モードが異なる固有ベクトル同士は互いに直交するという性質があるため(付録参照)、![]() 自由度モデルにおいて任意の変位ベクトルは個の固有ベクトルの線形和(重ね合わせ)で表せることになります(式19)。
自由度モデルにおいて任意の変位ベクトルは個の固有ベクトルの線形和(重ね合わせ)で表せることになります(式19)。
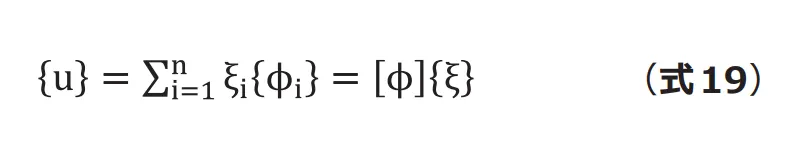
ここで{![]() }:物理座標系変位ベクトル、{
}:物理座標系変位ベクトル、{![]() }:モード座標変位(係数)ベクトル、
}:モード座標変位(係数)ベクトル、![]() の固有モードマトリクスです。このように固有モード情報を用いて物理座標とモー ド座標を相互に変換できます(図11)。
の固有モードマトリクスです。このように固有モード情報を用いて物理座標とモー ド座標を相互に変換できます(図11)。
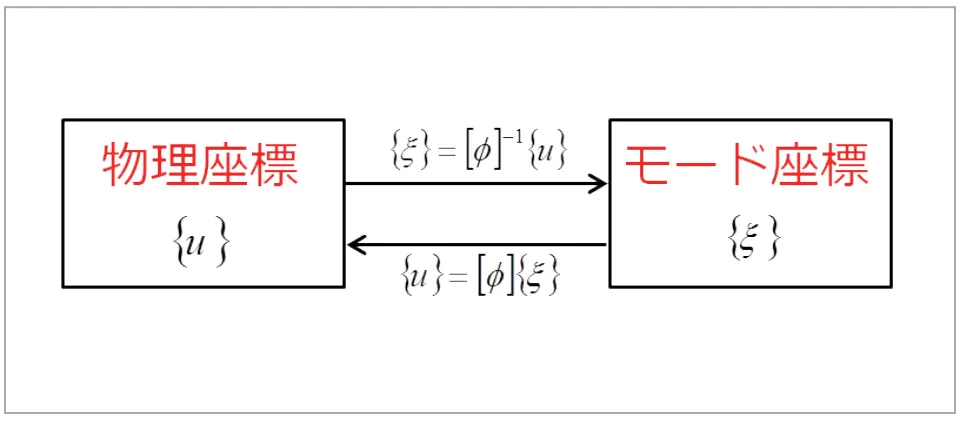
図11 物理座標とモード座標の変換
5.2 モード重ね合わせ法の基礎
モード重ね合わせ法では物理座標系の運動方程式をモード座標系に変換して計算します。そのため、モーダル解析を先に実施して固有モードを求めておく必要があります。
物理座標系の運動方程式(式20)に(式19)を代入して モード座標系に変換し、さらに左から![]() をかけると (式21)となります。
をかけると (式21)となります。
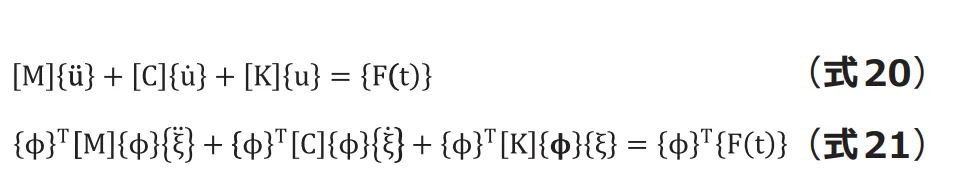
ここで、![]() はモードの直交性により
はモードの直交性により![]() となります(付録参照)。また減衰マトリクス
となります(付録参照)。また減衰マトリクス![]() に対しても直交性が成立すれば
に対しても直交性が成立すれば![]() となり(式22)を得ることができます。
となり(式22)を得ることができます。
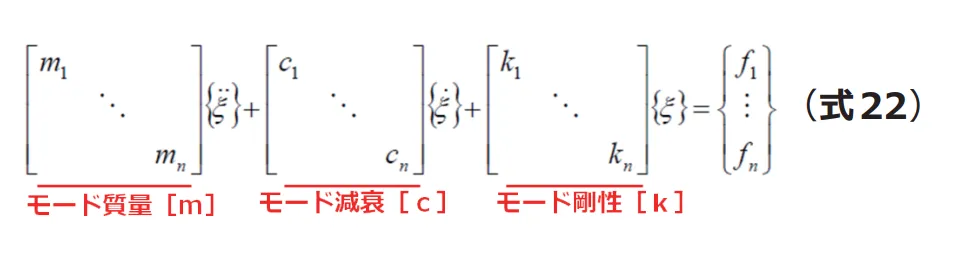
対角化された![]() により非連成な1自由度系運動方程式となり、連立方程式を解く必要がなくなり計算を高速化できます。また、低次の少数モードだけで全体応答を表現できると考えられる場合は、固有モードマトリクスを低次モードだけに絞ることにより、自由度を大幅に削減できます(たとえば1 万自由度のモデルを20次までのモードで表現すれば計算量が大幅に減ります)。
により非連成な1自由度系運動方程式となり、連立方程式を解く必要がなくなり計算を高速化できます。また、低次の少数モードだけで全体応答を表現できると考えられる場合は、固有モードマトリクスを低次モードだけに絞ることにより、自由度を大幅に削減できます(たとえば1 万自由度のモデルを20次までのモードで表現すれば計算量が大幅に減ります)。
(式22)からモード座標系の変位(係数)![]() が求まり、(式19)から物理座標系の変位に変換することができます。
が求まり、(式19)から物理座標系の変位に変換することができます。
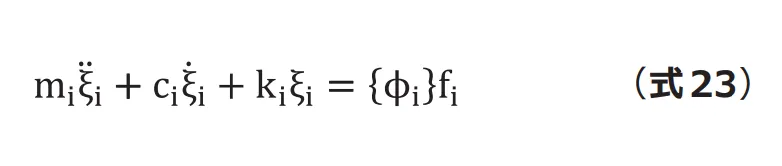
5.3 モード重ね合わせ法による2自由度系の非減衰強制振動の解析
では実際にモード重ね合わせ法を用いて、簡単な2自由度系の非減衰強制振動の計算をやってみましょう(図12)。
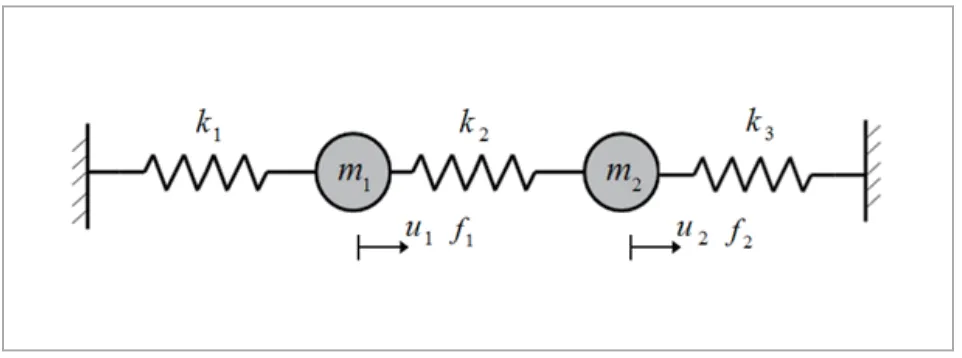
図12 2自由度非減衰強制振動
簡単化して![]() とすると、(式24) になります。
とすると、(式24) になります。
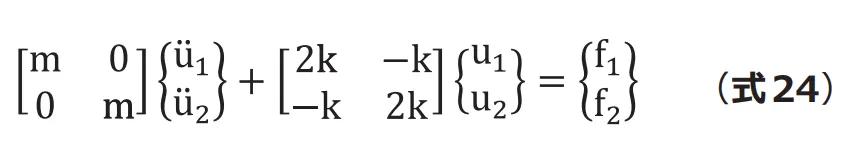
変位をモード座標系に変換します。先にモーダル解析を実施してあれば、第1 回の「4.3 2 自由度系の非減衰自由振動」で確認したとおり、
1 次モード 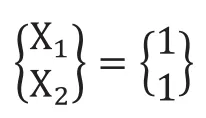
2 次モード 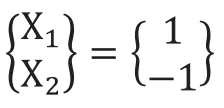
が既知であるため、固有モードマトリクスは![]() となります。先頭に
となります。先頭に![]() をつけたのは固有モードが比率だけに意味があるためです。これと(式19)を用いて(式21)からモード質量マトリクスを計算すると (式25)となります。
をつけたのは固有モードが比率だけに意味があるためです。これと(式19)を用いて(式21)からモード質量マトリクスを計算すると (式25)となります。
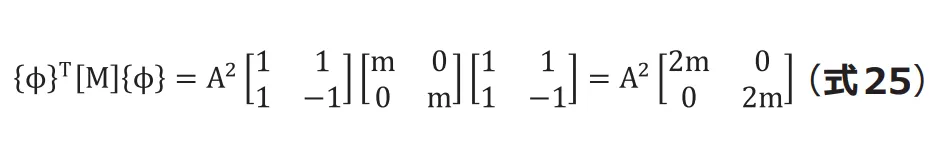
モード質量マトリクスを正規化して![]() になるようにするには、
になるようにするには、![]() であれば良いことがわかります。
であれば良いことがわかります。
同様にモード剛性マトリクスを計算すると(式26)とな ります。
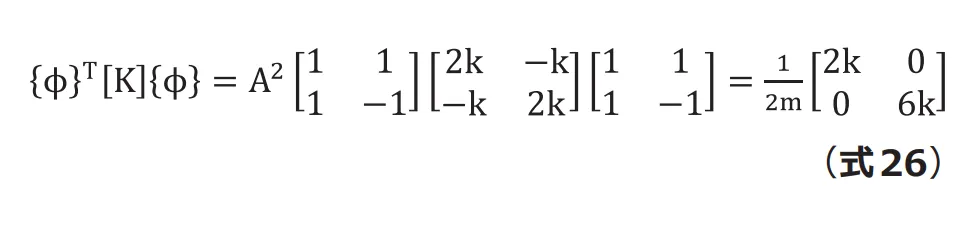
これらを(式23)に代入すると(式27, 28)になります。モード剛性マトリクスの部分に第1 回で求めた![]() および
および![]() の値が入っているのを確認してみてください。
の値が入っているのを確認してみてください。
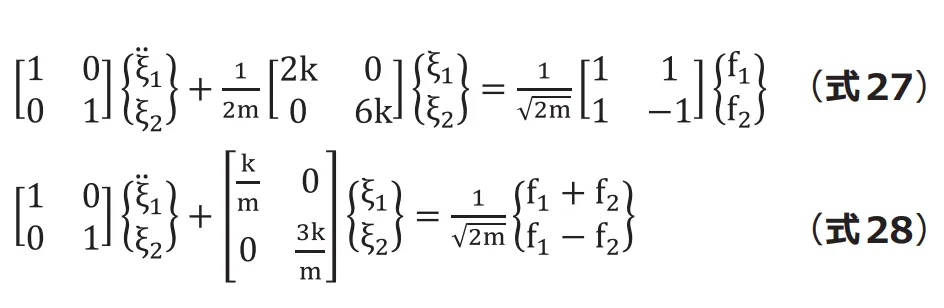
以上の式からモード変位![]() が求まり、物理座標系に変換すれば変位が求まります。先に確認したのと同様に、 この式は非連成な1 自由度系運動方程式であり、連立方程式を解く必要がありません。
が求まり、物理座標系に変換すれば変位が求まります。先に確認したのと同様に、 この式は非連成な1 自由度系運動方程式であり、連立方程式を解く必要がありません。
このことは、特に周波数を変えながら計算したい場合 に有利に働きます。フル法では周波数を変えるたびに逆行列を計算しなおす必要がありましたが、モード重ね合わせ法では非連成化した方程式を解くだけで済みます。最初にモーダル解析を実施しておくという手間はかかりますが、 全体でみれば計算時間を節約できるのです。そのため、特別な理由がなければモード重ね合わせ法を用いることが多いです。
5.4 モード重ね合わせ法とフル法の違い
モード重ね合わせ法とフル法の違いをまとめると以下のようになります。
モード重ね合わせ法
- 先にモーダル解析を行うため、系の特性をイメージしやすくなります。
- 高速に解を得ることができます
多自由度系の連立方程式を非連成化しているのと、高次モードの省略により計算負荷の低減を図れるためです。 - 少数モードだけで全体応答を表現できる場合に効果的です
周波数応答解析で評価したい周波数が0~200Hzであれば、モーダル解析で500Hzぐらいのモードまでとっておけば全体応答を概ね表現できると考えられます。以降のモードをカットすることで計算が高速になります。 - モードの打ち切り誤差が発生します
先の例では500Hz以降のモードをカットしましたので、それ以降のモードの影響は考慮されなくなります。複雑なモードでは、このことが精度に影響する可能性があります(この影響を緩和するために剰余剛性法という手法も存在します)。
フル法(直接法)
- 計算コストがかかります
多自由度系の連立方程式を直接計算するためです。 - 解析精度は高くなります
- 周波数依存性の材料特性を取り扱うことができます
粘弾性材料などの解析ではフル法が必要になります。
6 Ansysによる周波数応答解析
6.1 Ansysでの周波数応答解析手順
Ansysでは周波数応答解析を以下の手順で実施します。
- 3DCAD等からジオメトリデータを読み込む
- 適切な材料物性を設定する
- メッシュを作成する
メッシュの細かさの目安はモーダル解析と同様です(第1回参照)。 - 支持条件を設定する(必要に応じて)
- 加振力を定義する
- 解析したい周波数範囲を指定する
- 減衰を定義する(詳細は第3 回で解説します)
- 解析を実行し結果を確認する
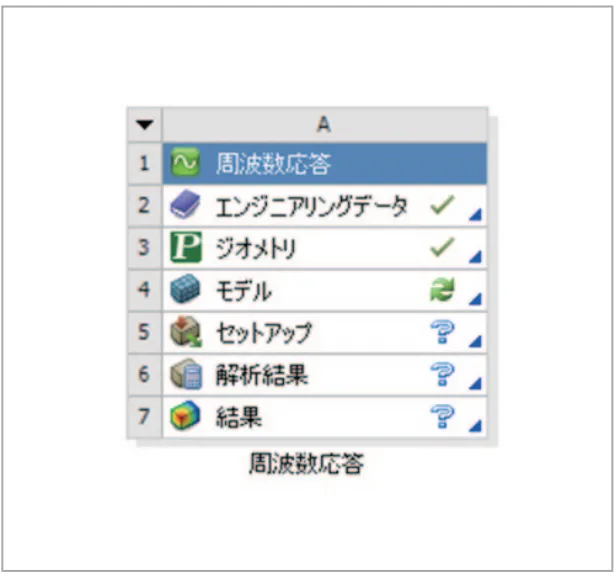
図13 内部的にモーダル解析を実施する方法
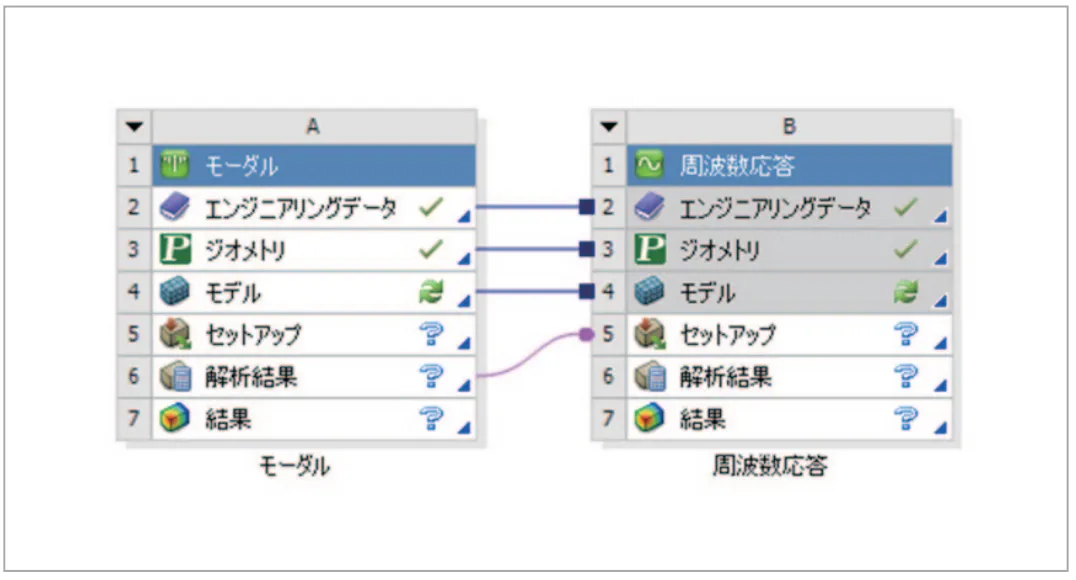
図14 事前にモーダル解析を実施する方法
6.2 加振力の定義
構造物を加振したい位置に加振力を設定します。通常は力荷重で定義します。複数の荷重があり位相が異なる場合は位相角を指定します。実部-虚部による指定も可能です (図15)。
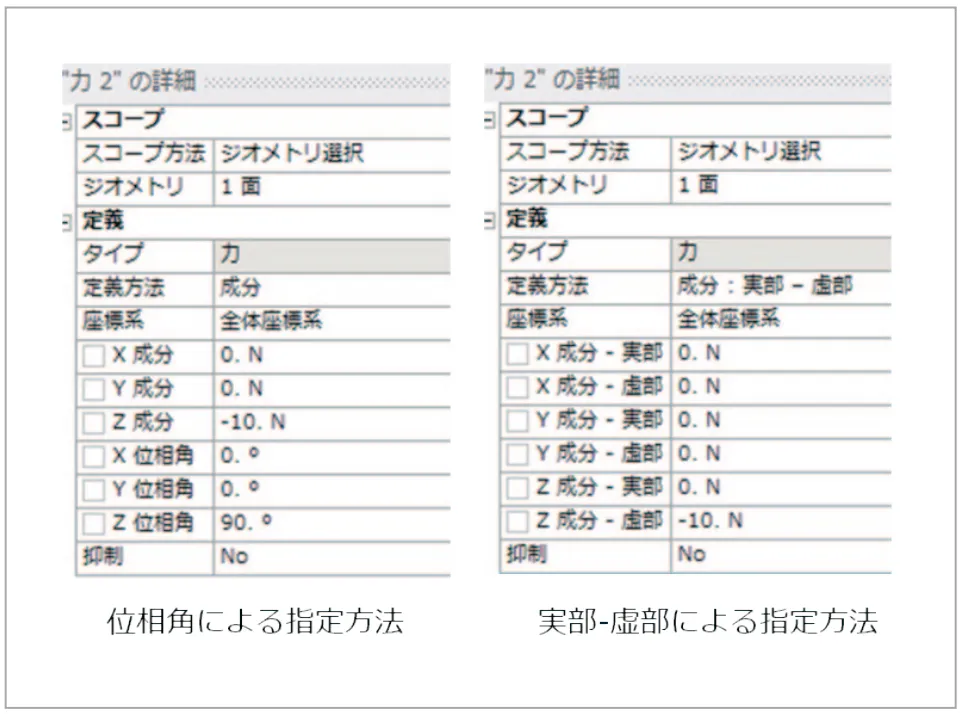
図15 加振力の定義
6.3 加速度加振の定義
(図16)のように振動試験や地震波に対する構造物の応答を評価するときには、基部加振を使用します。基部加振とはモデル全体ではなく、モデルの一部の面に対して加速度または変位を使用して強制加振を定義する手法です。 モード重ね合わせ法では強制運動法(Enforce Motion Method、略称EMM)という手法が一般的に用いられます。 強制運動法では基部に固定条件を定義した上で(図17)のように加速度を設定します。
一方、フル法では強制運動法は対応しておらず、ラージマス法(Large Mass Method、略称LMM、大質量法とも呼ぶ)が用いられます。ラージマス法の設定方法につ いては、お手数ですが弊社サポートサイトのFAQをご覧ください。
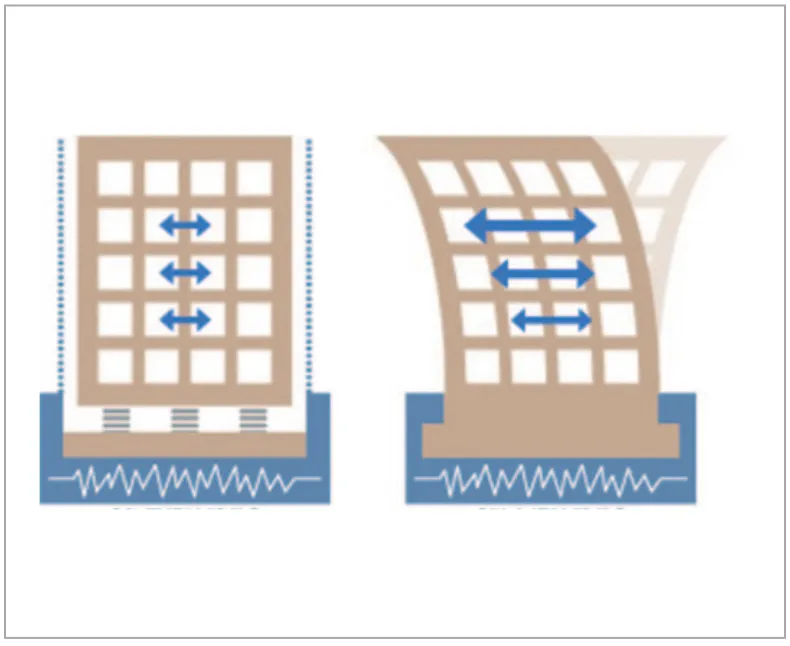
図16 基部加振のイメージ

図17 強制運動法の設定
6.4 解析設定
解析設定では、モード重ね合わせ法とフル法の選択のほか、周波数範囲や計算間隔の指定ができます。(図18)はモード重ね合わせ法で0~1000Hzまで50等分、つまり20Hz間隔で解析することを示しています。周波数範囲の指定方法には様々あり、共振周波数近傍で細かく計算させる「クラスタ解」という手法もあります(モード重ね合わせ法のみ)。
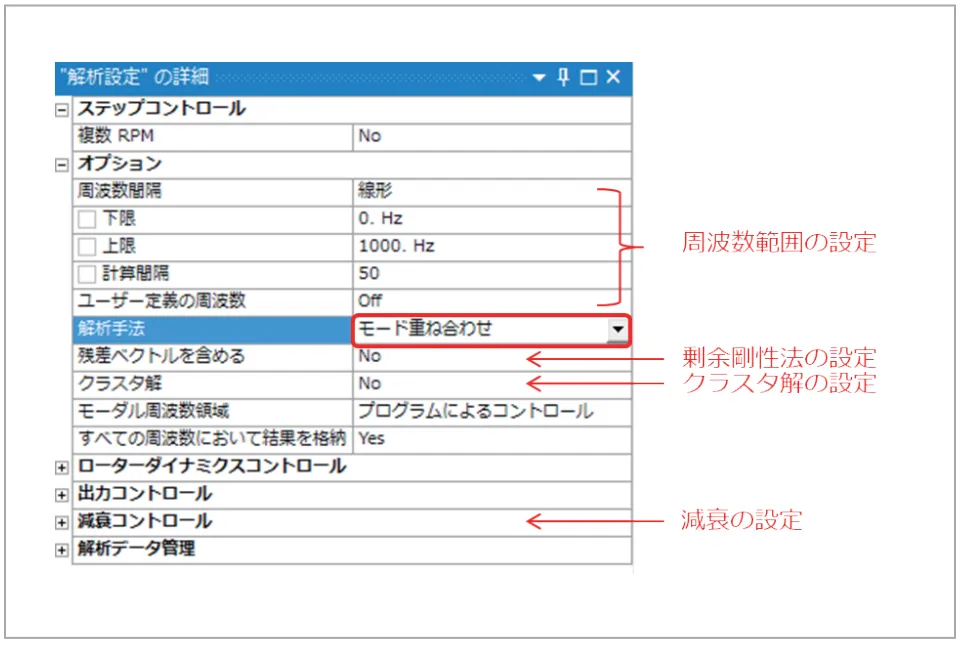
図18 周波数応答の解析設定
6.5 解析結果の確認
周波数応答解析ではコンター図だけでなくグラフ結果も合わせて見ることが多いです。グラフ結果では任意の位置にて、変位や加速度などの振幅vs.周波数グラフや位相vs.周波数グラフを表示できます。(図19)は先端位置での 加速度振幅と位相を表示したグラフで、700Hz付近に1 次 モードがあり位相が反転する様子が観察できます。
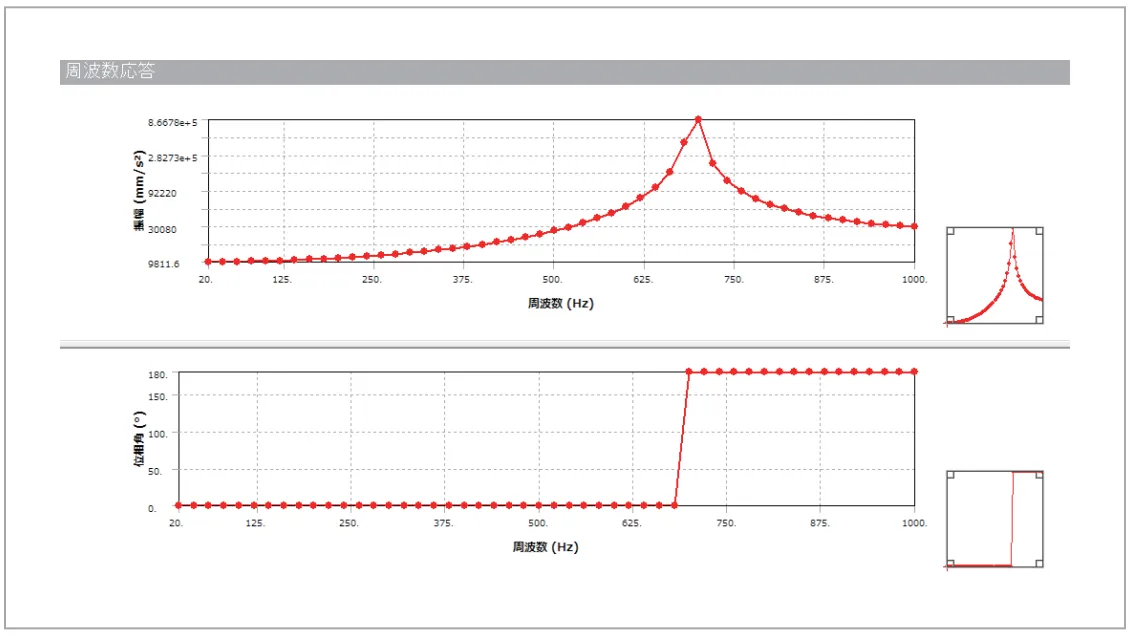
図19 加速度振幅 vs. 周波数グラフと位相 vs. 周波数グラフ
コンター図を表示するときには2通りの方法があります。 1 つめは位相を指定する方法で、結果を見たい周波数と位相(スイープフェーズ)を指定します。変位の評価でよく使われます。2 つめは全位相における最大値で結果表示する 方法で、応力の評価でよく使われます(図20)。

図20 変位図とミーゼス応力図
7 Ansys周波数応答解析事例
(図21)はPCB基板の加速度試験を周波数応答解析で模擬した事例です。試験は加速度でサインスイープ加振を行い、基板全体の動的挙動を評価します。はじめにモーダル解析によりPCB基板の共振周波数および固有モードを確認します。加速度加振は強制運動法を用いてエッジコネクタに加速度を直接定義した周波数応答解析を実施しています。
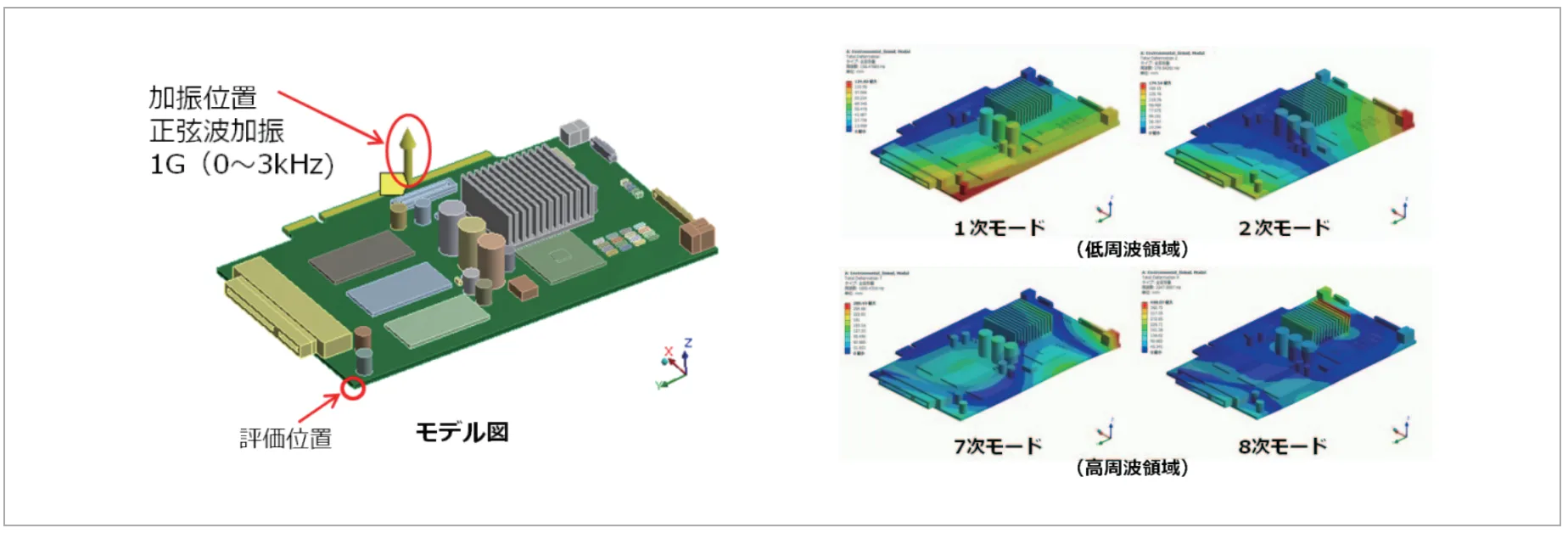
図21 PCB基板の加速度試験
8 付録
8.1 複素指数関数
振動現象は複素指数関数![]() で表現することが 多いです。普通、振動といえば
で表現することが 多いです。普通、振動といえば![]() や
や![]() などの三角関数 を思い浮かべますので、一見すると無関係のように見えま すが、オイラーの公式を使うと三角関数と複素指数関数は 元来同じものであり相互に変換することができます。 まず1 次元無減衰系の振動状態を三角関数で表してみます。
などの三角関数 を思い浮かべますので、一見すると無関係のように見えま すが、オイラーの公式を使うと三角関数と複素指数関数は 元来同じものであり相互に変換することができます。 まず1 次元無減衰系の振動状態を三角関数で表してみます。
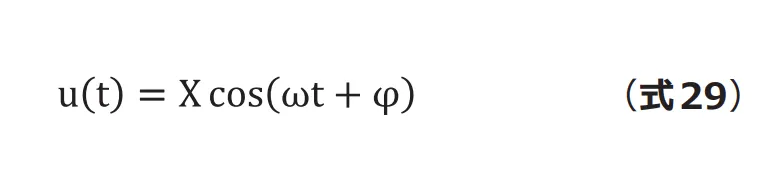
ここでオイラーの公式(式30)を用います。
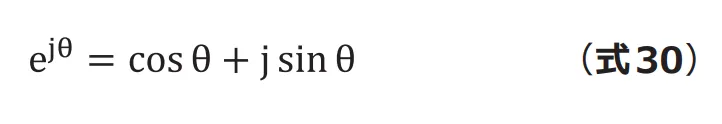
![]() は次のように表せます。
は次のように表せます。
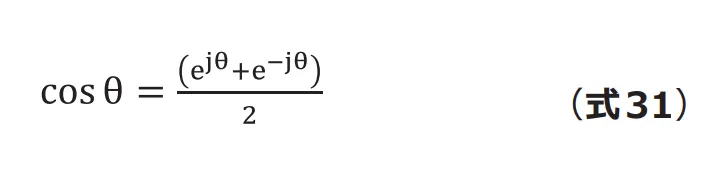
したがって変位は
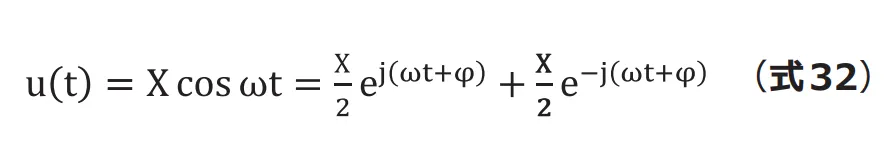
となり、三角関数と複素指数関数が変換できることがわかります。厳密にはこれが正しい表現ですが一般的には![]() という表現が用いられています。
という表現が用いられています。
この複素指数関数がどのように振動を表しているかを考え てみます。横軸に実部、縦軸に虚部をとった複素平面(図22) を考えてみます(図は簡単化して![]() としています)。
としています)。
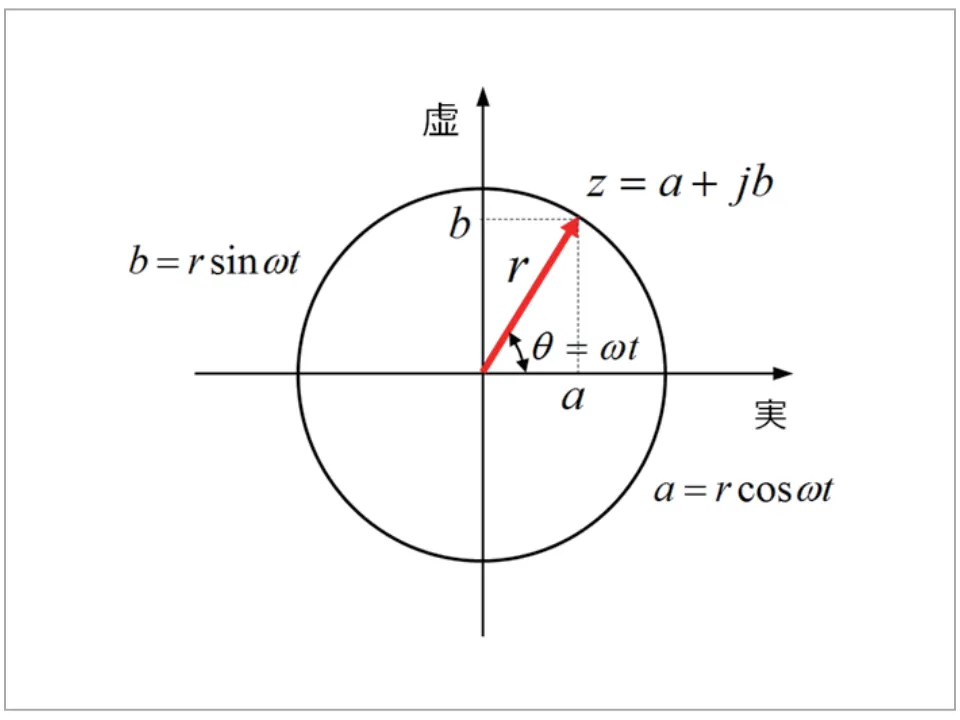
図22 複素数と複素指数関数
赤い矢印で示した座標は、![]() とすると実部が
とすると実部が![]() で、虚部
で、虚部![]() がになりま す。また
がになりま す。また![]() 、
、![]() です。
です。![]() の値を連続的に変化させながらプロットすると図に示した円運動となり ます。これは大きさ
の値を連続的に変化させながらプロットすると図に示した円運動となり ます。これは大きさ![]() と偏角
と偏角![]() という2個の互いに独立な素からなる2次元次数ですので、1個の式で表すことができて
という2個の互いに独立な素からなる2次元次数ですので、1個の式で表すことができて
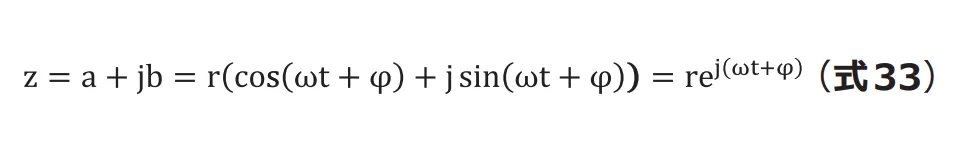
となります(最後にオイラーの公式を用いています)。
この円運動の実部だけを取り出してプロットすると、 (図23)に示すような振動現象になります(図は簡単化して![]() としています)。複素指数関数を用いることで、振動 という現象を1個の数で完全に表現できるので便利です。指数関数は微分計算が非常に簡単というメリットもあります。 ここでみたとおり、複素指数関数で振動を表現する場合、いつも実部だけが実際起こっている現象を表現しており、虚部は現象として意味を持たないと考えてください。
としています)。複素指数関数を用いることで、振動 という現象を1個の数で完全に表現できるので便利です。指数関数は微分計算が非常に簡単というメリットもあります。 ここでみたとおり、複素指数関数で振動を表現する場合、いつも実部だけが実際起こっている現象を表現しており、虚部は現象として意味を持たないと考えてください。
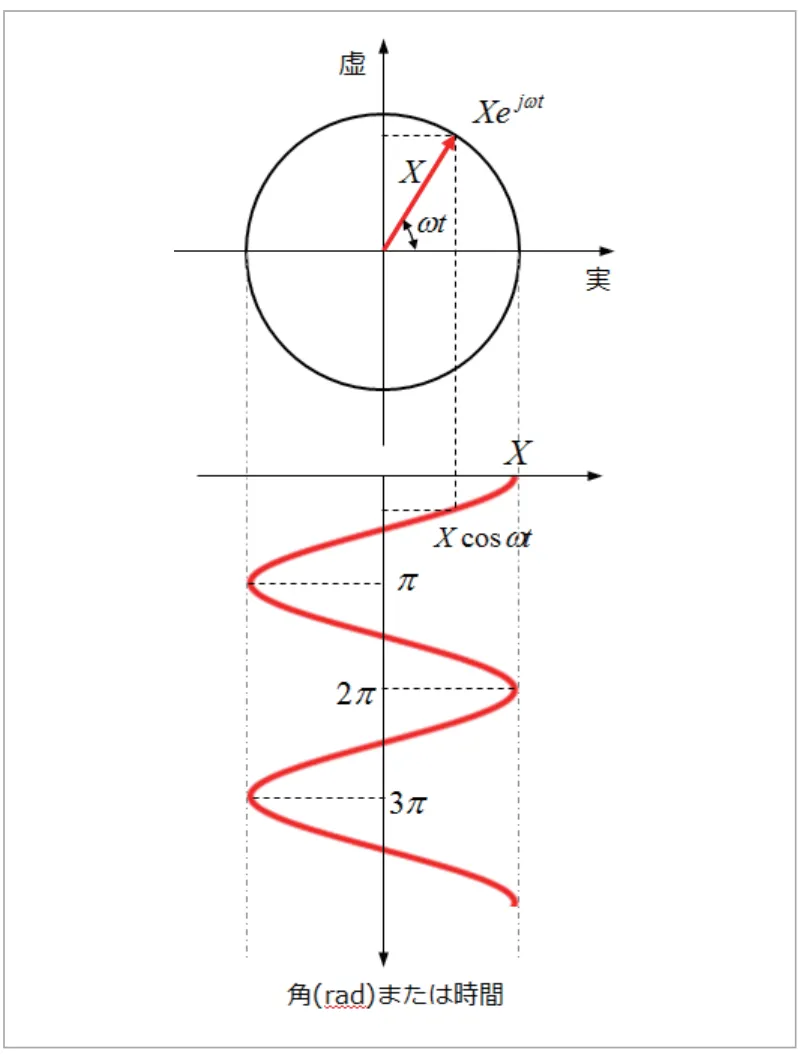
図23 振動現象の2つの表現
8.2 固有ベクトルの直交性
ベクトル![]() が直交するのであればベクトルの内積はゼロ、つまり
が直交するのであればベクトルの内積はゼロ、つまり![]() となります。これを
となります。これを![]() と解釈し、
と解釈し、![]() のとき重み
のとき重み![]() で直交するとしたのが広義の直交性の定義です。
で直交するとしたのが広義の直交性の定義です。
これを踏まえて、第1回の多自由度系の非減衰自由振動の式から固有ベクトルの直交性を確かめてみます。![]() と
と![]() が固有振動数、
が固有振動数、![]() と
と![]() が固有ベクトルとすると次式が成り立ちます。
が固有ベクトルとすると次式が成り立ちます。
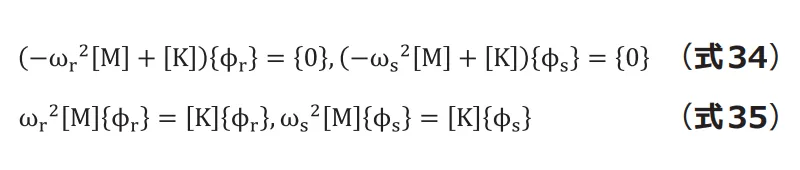
ここで![]() ,
,![]() をそれぞれ左からかけます。
をそれぞれ左からかけます。
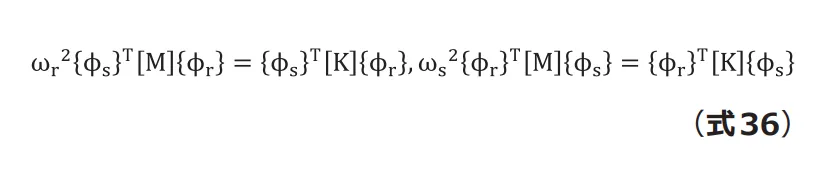
ここで![]() は対角行列、
は対角行列、![]() は対称行列であることから次式に変形できます。
は対称行列であることから次式に変形できます。
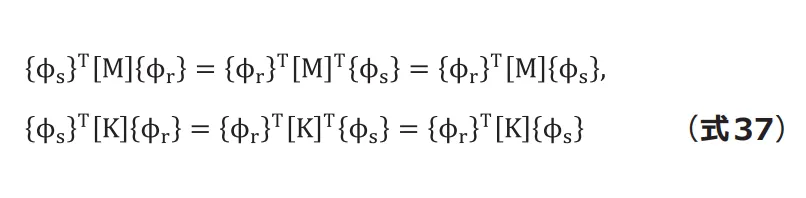
これを(式36)の第1式に代入した後で、第2式との差分をとると次式になります。
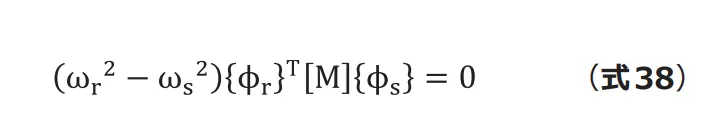
ここで![]() とすれば明らかに
とすれば明らかに![]() であるため
であるため![]() が成立します。よって広義の直交性の定義から、固有ベクトル
が成立します。よって広義の直交性の定義から、固有ベクトル![]() と
と![]() は直交性を持つことが確認できます。
は直交性を持つことが確認できます。
逆に![]() の場合、
の場合、 ![]() を定義でき、それぞれ「モード質量マトリクス」「モード剛性マトリクス」と呼びます。これらは対角マトリクスになっています。ちなみにAnsysのモーダル解析結果で表示される変位量
を定義でき、それぞれ「モード質量マトリクス」「モード剛性マトリクス」と呼びます。これらは対角マトリクスになっています。ちなみにAnsysのモーダル解析結果で表示される変位量![]() はとなるように正規化したものです。
はとなるように正規化したものです。
9 おわりに
参考文献
[1] 一般社団法人 日本機械学会 計算力学技術者資格認定事業委員会
(https://www.jsme.or.jp/cee/)
[2] Ansysオンラインヘルプ > 構造解析ガイド > 周波数応答解析
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-
剥離・接合強度評価ソリューション ~Ansys Workbench Mechanicalで実施できる剥離解析~
-

レーザー集光の高温レンズ歪みを克服するAnsys連携ソリューション
-
周波数応答解析×自動抽出で干渉チェックを高速化
-

直観的な操作で無線/デジタルフィルタの設計・最適化を支援する〜Ansys Nuhertz FilterSolutions〜
-
流体機器設計の新たな一歩
~Ansys Discoveryで加速する設計改革~
-
筐体の冷却性能を構想設計から見える化 (手戻りを削減できる)
~Ansys Discoveryで始める電気筐体製品の設計改革~
-
若手でもすぐに使えるリアルタイム解析 (勘と経験からの脱却)
~Ansys Discoveryによる30名規模メーカーの設計改革~
-
構想設計ですぐにリアルタイム検証 ~解析専任者ゼロでも使いこなせるAnsys Discovery~
~解析専任者ゼロでも使いこなせるAnsys Discovery~