CAEを学ぶ
はじめての振動解析(1)振動の基礎とモーダル解析
はじめての振動解析(1)振動の基礎とモーダル解析 の概要

はじめての振動解析(1)(2)(3) 完全保存版 PDF を無料公開中

はじめての振動解析(1)(2)(3) 完全保存版 PDF サンプル
これさえ読めば振動解析の基本がわかる!
全3回のシリーズとなっております「はじめての振動解析」について、3回分の解析講座を1冊でお読みいただける完全保存版 PDF を公開いたしました。どなたでも簡単なフォーム入力のみでダウンロードいただけますので、是非この機会にご利用ください。
ページ数:30ページ
ファイル形式: PDF
1 はじめに
これはCAEの世界でも同様で、たとえば一般社団法人日本機械学会が主催する計算力学技術者資格認定事業[1]において、構造解析の資格認定が「固体力学分野」と「振動分野」の2つに分かれていることからも振動解析の重要性が伺い知れます。
本稿ではCAEではじめて振動解析に取り組まれる方向けに、モーダル解析・周波数応答解析・モード重ね合わせ法・減衰といった振動解析の基礎知識を3 回にわたる連載でご紹介いたします。
2 振動のメカニズム
振動はどのように発生するのでしょうか? 静的な力を加えても振動は発生しませんが、たとえば構造物を叩くとか揺するなど時間変化する力が加えられると何らかの振動が発生するでしょう。このような振動を発生する源になる外力を加振力と呼びます。
加振力が異なれば発生する振動が変わるのは直感的に理解できると思います。しかし、同じ加振力を加えたとしても構造物の特性により発生する振動は異なります。たとえば水の入ったコップを叩いたとします。同じ力で叩いても水が少なければ高い音(=周波数が高い)、水が多ければ低い音(=周波数が低い)になるでしょう。つまり構造物の質量により振動状態は異なるわけです(図1)。
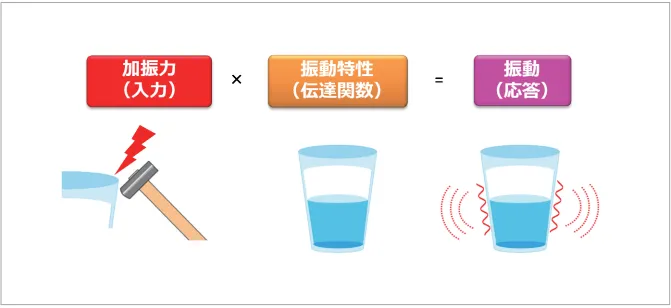
図1 振動のメカニズム
次にギターのような弦楽器を弾いたとします。弦が強く張ってあれば高い音、たるんでいれば低い音になるでしょう。つまり構造物の剛性によっても振動状態は異なるわけです。
このように、発生する振動は加振力と構造物の振動特性から決まります。そして構造物の振動特性は、主に構造物の質量と剛性が影響します(図2)。
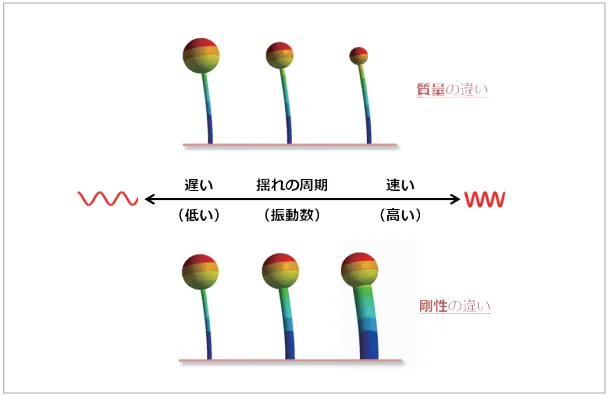
図2 振動特性
3 振動解析の基礎
前述のとおり、発生する振動は加振力と構造物の振動特性から決まります。CAEで行う振動解析では、形状や材料特性や支持条件等から構造物の振動特性が表現され、設定した加振力に基づき構造物の振動応答を計算することができます。
まずは簡単な1自由度系モデルの基礎方程式から、静解析と動解析の違いを見ていきます。
3.1 静解析と動解析
CAEの構造解析で最もよく使われるのが静解析(静的構造解析)です。変形や応力分布から強度を評価します。また、非線形性(材料や接触)を考慮し、局所的な変形挙動を評価することもあります。静解析では静的なつり合い状態を仮定し、慣性の影響は無視して、外力と内力のつり合いを解きます。基礎方程式は(式1)のようになります。
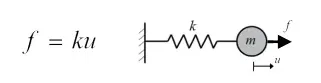
式1 静解析の基礎方程式
一方、動解析では構造全体の振動挙動を評価(製品の性能・品質評価)したり、共振周波数、周波数および時間軸で変位/速度/加速度を評価したりすることが多いです。
動解析では動的なつり合い状態、つまり時間とともに変動する振動現象や外力が変化する現象を仮定し、変位が時間の関数で運動している状態を表す(式2)のような運動方程式を解きます。静解析では考慮されていなかった慣性力や減衰力の項が追加されています。
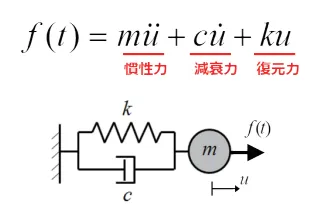
式2 動解析の基礎方程式
有限要素法では連続体を要素分割して領域で離散化し、(式3)の運動方程式を数学的に解くというのが基本的な考え方になります。

式3 有限要素法の動解析の基礎方程式
3.2 解析タイプ
(式3)の運動方程式をそのまま解いても良いのですが、実はそのまま解くと計算コストが非常に高くなります。たとえば、周期的な外力に対して物体が定常振動する様子を見たいと思った場合、普通に運動方程式を解くと、止まっている状態から動き出して一定の周期で振動する状態になるまでひたすら計算し続ける必要があり、無駄が大きくなります。
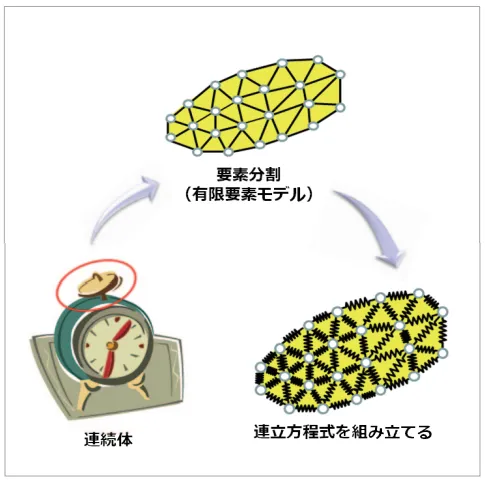
図3 有限要素法のイメージ
また、減衰を無視した構造物の振動特性だけ評価したい場合は、減衰項と外力項をなくした式で計算コストを抑えて解析できるはずです。このような様々なニーズに合わせて効率的に計算するために、動解析にはいくつかの解析タイプが用意されています。よく使われる解析タイプをご紹介します(図4)。
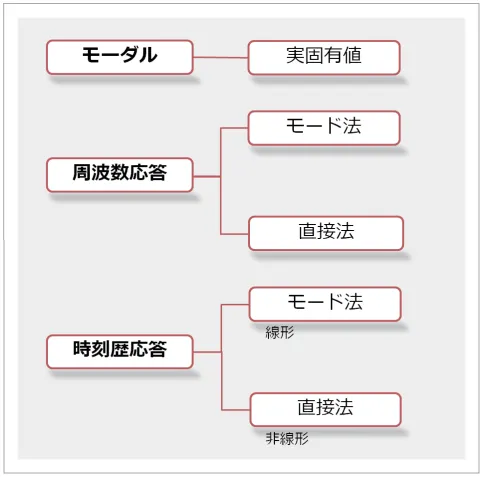
図4 よく使われる解析タイプ
本稿では「モーダル解析」についてご説明いたします。「周波数応答解析」は次回(第2 回)で取り上げる予定です。「時刻歴応答解析」は本シリーズでは割愛させていただきます。ちなみに「時刻歴応答解析」の「直接法」が、運動方程式をそのまま解く手法になります。
モーダル解析(固有値解析)
4.1 モーダル解析とは?
モーダル解析は固有値解析とも呼ばれます。振動解析において最も基本的な解析タイプで、構造物そのものが振動しやすい周波数とその振動形状を調べる解析です。振動特性を求める解析ともいえます。加振力を考慮しない自由振動状態を計算します(加振力を考慮して振動応答を計算するには周波数応答解析がよく用いられます)。
構造物の特性を求めるだけなので計算は高速です。モー ダル解析で絶対に理解しておかなければいけないのが「固有振動数」と「固有モード」です。
4.1.1 固有振動数
固有振動数とは、構造物が持つ固有の共振周波数です。固有振動数を具体的にイメージするため、たとえば夏祭りの屋台などで見かける水ヨーヨー風船(風船に水をつめてゴムひもを結んだおもちゃ)を思い浮かべてみてください。
ゴムひもを手で持って適当に上下に振っただけだとあまり振動しませんが、ある周期で振ると大きく振動します(図5)。これは手の動き(加振力)の周波数と、水ヨーヨー風船が持つ固有振動数が一致する(共振する)ことで発生していると考えられます。共振が発生すると大きな振動が発生し、構造物が損傷する危険がありますので、固有振動数は共振現象を回避する上で必要不可欠な値となります。
固有振動数は形状、材料特性および支持位置によって異なります。したがって、同じ形状・材料であっても支持条件を設定する箇所を変えると固有振動数は変わります。先の水ヨーヨー風船の例でいえばゴムひもを持つ位置を変えると固有振動数が変わるというイメージです。CAEツールで解析すると、固有振動数が○○Hzといった結果が出てきます。
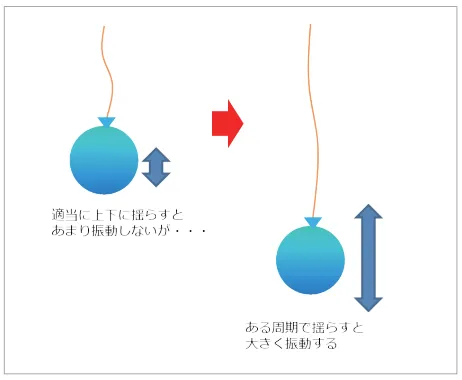
図5 水ヨーヨー風船にみる固有振動数
4.1.2 固有モード
固有モードとは、固有振動数においてどのように振動するかを表す変形形状のことです。先の例でいえば、水ヨーヨー風船が上下に振動している様が固有モードとなります。
実際にCAEツールで解析すると、変形図やアニメーショ ンで固有モードを確認できます(図6)。勘違いしやすいの ですが、CAEツールが表示する変位量は物理量ではなく相 対的なものであるため数値に物理的意味はありませんので注意してください。前述のとおりモーダル解析は加振力を 考慮しないので振動応答が求められないためです。
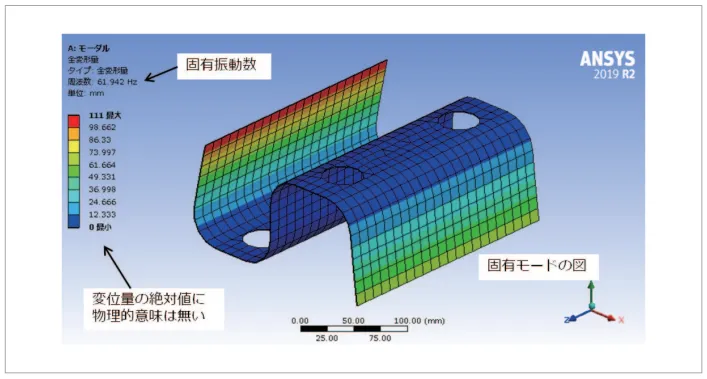
図6 Ansysのモーダル解析結果例
4.2 1自由度系の非減衰自由振動
先ほどは直感的なイメージで固有振動数を説明しましたが、(図7)で示す簡単な1 自由度モデルで固有振動数を理 論的に求めてみます。
このモデルで非減衰自由振動の条件は、加振力![]() および減衰
および減衰![]() となります。バネを引張りリリースすることによって起こる定常振動状態の運動方程式は(式4)のようになります。
となります。バネを引張りリリースすることによって起こる定常振動状態の運動方程式は(式4)のようになります。
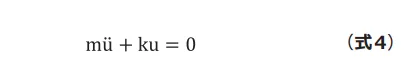
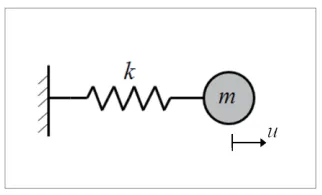
図7 1自由度非減衰自由振動
ここで![]() と仮定します。
と仮定します。![]() は複素数、
は複素数、![]() は角振動数です。なぜ振動状態がこのように表されるのかは第2回で説明しますが、ここでは角振動数で同じ値を繰り返す調和振動は計算の都合上、複素指数関数で表現するのが便利だと覚えていただければ結構です。
は角振動数です。なぜ振動状態がこのように表されるのかは第2回で説明しますが、ここでは角振動数で同じ値を繰り返す調和振動は計算の都合上、複素指数関数で表現するのが便利だと覚えていただければ結構です。
代入して整理すると(式6)のようになります。(式6)が 満たされる条件は![]() または
または![]() ですが、 前者は振動しないことを意味するため後者が解となります (式7)。
ですが、 前者は振動しないことを意味するため後者が解となります (式7)。
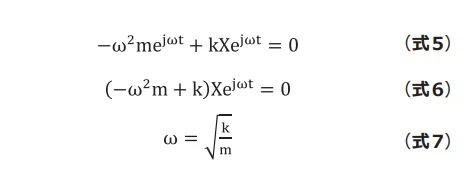
自由振動はバネの引張り量に関係なく決まった振動数で 周期運動することがわかります。この振動数を固有振動数 (または固有角振動数)と呼びます。
(式7)で示されるとおり、固有振動数は剛性が高くなるか質量が小さくなるほど上昇します。逆に剛性が低くなるか質量が大きくなるほど固有振動数は低下します。これは振動問題を考える上でとても重要ですので、ぜひ覚えておきましょう。
4.3 2自由度系の非減衰自由振動
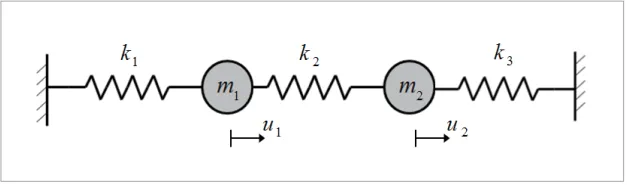
図8 2自由度非減衰自由振動
続いて2自由度系(図8)でも同様に固有振動数を計算してみます。各質点に対して運動方程式を立てると(式8)のようになります。
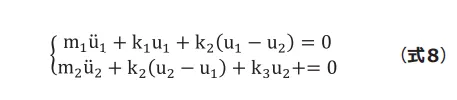
![]() と
と![]() についてまとめると(式9)のようになります。
についてまとめると(式9)のようになります。
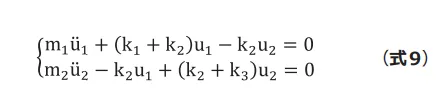
(式9)を行列とベクトルで表します。簡単化して、![]() とすると(式10)に なります。
とすると(式10)に なります。
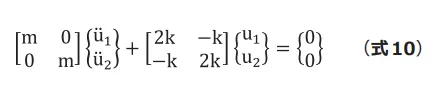
先ほどと同様に変位を複素指数関数(式11)で仮定し、(式10)に代入すると(式12)となります。(式12)は固有方程式と呼ばれます。
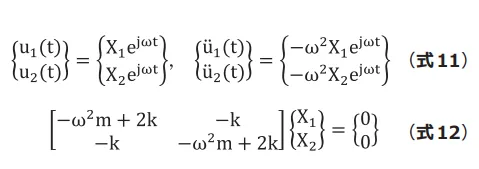
振動中![]() は
は![]() はにならないため非自明な解が存在する条件は(式13)になります。これを特性方程式と呼びます。
はにならないため非自明な解が存在する条件は(式13)になります。これを特性方程式と呼びます。
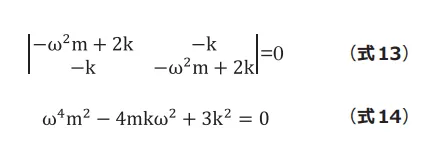
(式13)は(式14)のように書けて、これを解くと( ![]() は 正の値なので)2 つの解が得られます。(式15)
は 正の値なので)2 つの解が得られます。(式15)
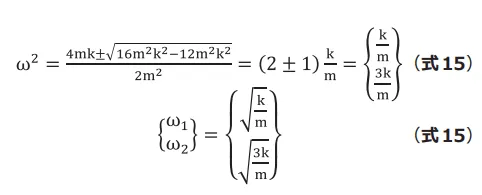
2自由度の場合、2個の固有振動数が求まります。このように固有振動数はモデルの自由度の数だけ求まります。
なお、振動数の低いほうから1 次モード、2 次モード...と 呼びます。
続いて(式15)を(式12)に代入して![]() および
および![]() を求めてみます。まず
を求めてみます。まず![]() に
に![]() を代入してみると(式16)となります。
を代入してみると(式16)となります。
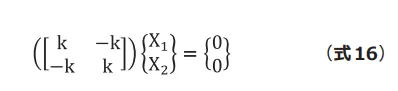
解は自明で![]() です。これを固有モード(ベクトル) と呼びます。ここで注目していただきたいのは
です。これを固有モード(ベクトル) と呼びます。ここで注目していただきたいのは![]() と
と![]() の比率だけが重要であるという点です。
の比率だけが重要であるという点です。
![]() でも
でも ![]() でも(式16)は成立します。先ほどモーダル解析で得られる変位量は物理量ではなく相対的なものであると説明しましたが、その理由はここにあるわけです。
でも(式16)は成立します。先ほどモーダル解析で得られる変位量は物理量ではなく相対的なものであると説明しましたが、その理由はここにあるわけです。
続いて![]() に
に![]() を代入してみると(式17)となります。
を代入してみると(式17)となります。
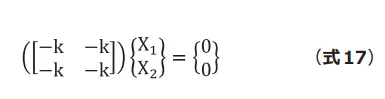
解は自明で![]() です。ここでも比率だけが重要であることを確認してください。
です。ここでも比率だけが重要であることを確認してください。
以上の結果を図で表すと(図9)のようになります。2自由度系では2 つの固有振動数と固有モードが得られます。 モードは自由度の数だけ存在します。
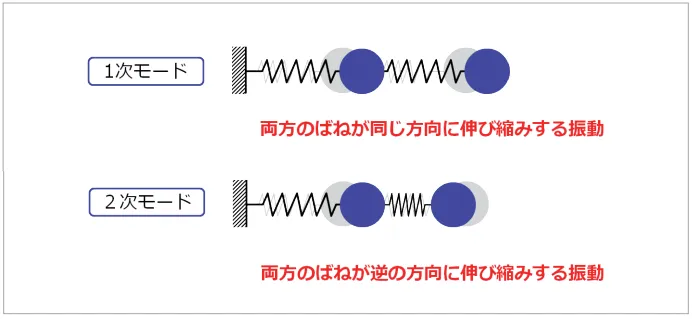
図9 2自由度系の固有モード
4.4 多自由度系の非減衰自由振動
多自由度系に拡張すると運動方程式は(式18)のようになります。
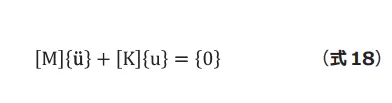
2自由度系の場合と同様に変位を(式19)のように複素指 数関数で仮定して固有方程式を求めると(式20)となりま す。非自明な解が存在する条件は(式21)で、これを解け ば固有振動数が求められます。
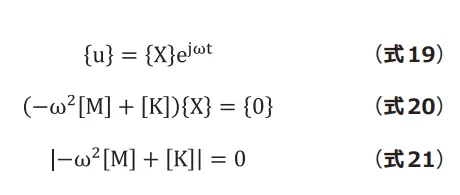
そして(式20)を満たすベクトル![]() が固有ベクトルとなります。固有振動数や固有モードは自由度の数だけ求められますが、すべてのモードを計算すると計算量が膨大になるため、CAEでは求めるモード数を指定して解析を行います。また、ブロックランチョス法やサブスペース法などの効率的な解法が用いられるのが一般的です。
が固有ベクトルとなります。固有振動数や固有モードは自由度の数だけ求められますが、すべてのモードを計算すると計算量が膨大になるため、CAEでは求めるモード数を指定して解析を行います。また、ブロックランチョス法やサブスペース法などの効率的な解法が用いられるのが一般的です。
モーダル解析でできること
- 構造物の固有振動数を把握
周期的に変動する外力に対して共振を避けるための対策が可能になります。たとえば構造物に取り付けられているモータが0~50Hzで回転するとしたら、構造物の固有振動数を50Hzよりも(少し余裕をみて)大きくしておけば共振を避けることができます。 - 構造物の固有モード(変形形状)を把握
変形形状を確認することで振動を抑制する対策が立てや すくなります。(図10)のようにパネルがペコペコと振 動する固有モードが出ているようであれば、リブを立て て面の振動を抑えることが有効な対策と考えられます。 CAEを活用すればすぐに対策の効果を検証できます。よりアドバンスな使い方として、重要なモードを「刺激係数」や「有効質量」といった数値でモード情報を把握することもできます。これらはどの方向に振れやすいか(振動しやすいか)を示す指標です。Ansysではソルバーアウトプットで確認できます。
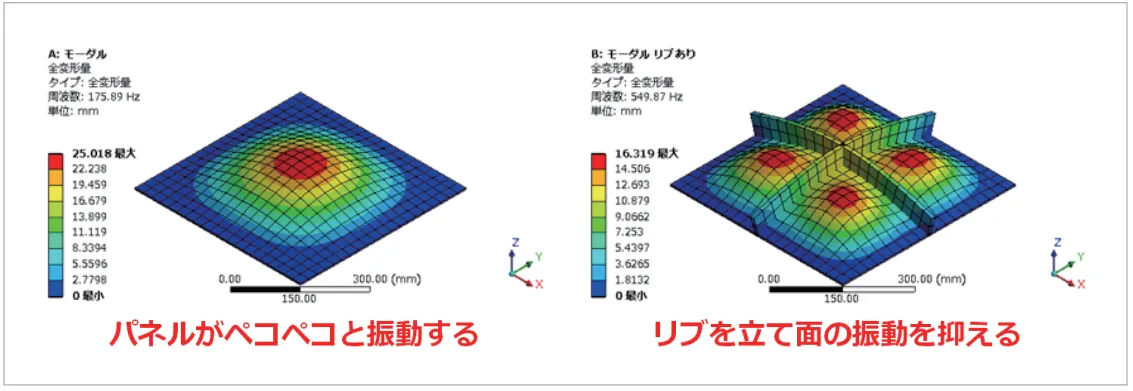
図10 固有モードによる振動抑制方法の検討例
6 Ansysによるモーダル解析
6.1 Ansys でのモーダル解析手順
- 3DCAD等からジオメトリデータを読み込む
- 適切な材料物性を設定する
前述のとおり振動特性には剛性と質量が大きく影響しますので、ヤング率と密度は実物に即した適切な値を入力する必要があります。
もし形状を簡略化している場合は、解析モデルと実物の質量が異なってしまうかもしれません。無視できないほど異なる場合は、実物と同じ質量になるように密度を調整することもあります。 - メッシュを作成する
モーダル解析は応力を見る解析ではないので、応力集中部にメッシュを細かく切るといった工夫は必要ありませんが、固有モードが表現できるレベルのメッシュは必要です。一般的に固有モードの腹に対して10 分割程度が目安といわれています。 - 支持条件を設定する(設定しなくても良い)
前述のとおり振動特性は支持位置によっても変わりますので、よく検討して設定する必要があります。
モーダル解析は振動特性を求めるだけで力の釣り合いは解かないため、静的構造解析とは異なり支持条件が無くても解析できます。支持条件が無い場合、剛体モードが検出されます。(後述) - 計算するモード次数を設定する
モード次数が多すぎると計算に時間がかかるため、少なすぎず多すぎずの値を設定してください。初回の計算では様子を見るため6~30ぐらいが適切だと思います。 - 解析を実行し、固有振動数と固有モードを確認する
周辺を固定したプレートで実際にモーダル解析を実施し た例を(図11)に示します。次数が高くなるほど複雑なモー ドになります。
複雑なモードを解析したい場合はメッシュにも注意が必 要です。メッシュによる比較を(図12)に示します。メッシュが粗いと9~10 次モードで大きな差が生じていること がわかります。
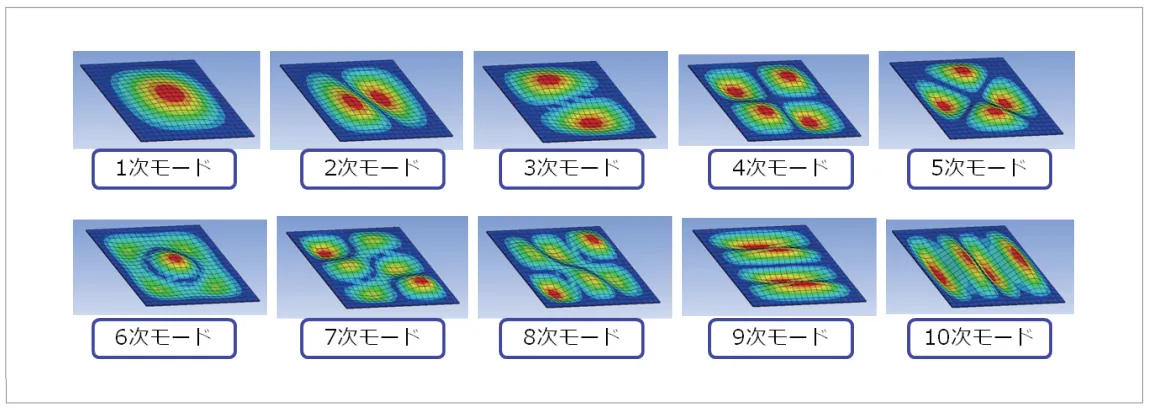
図11 プレートのモーダル解析例
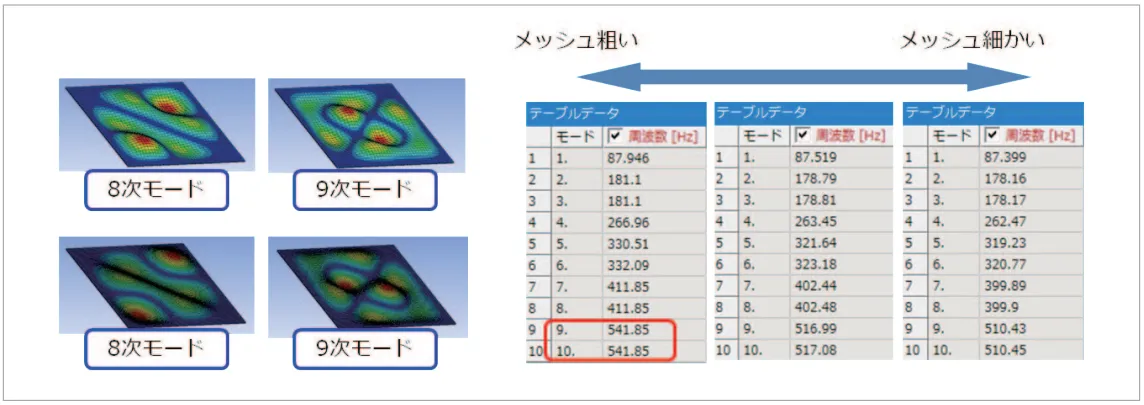
図12 メッシュサイズによる比較
6.2 剛体モード
モデルに支持条件を設定せずに解析すると、支持されていない自由度方向について剛体モードが検出されます。剛体モードとは構造物が剛体移動するモードで、固有振動数は0Hz付近となります。先の1 自由度系で出てきた(式6) の解が![]() となった状態といえます。通常は剛体モード は結果評価の対象としません。
となった状態といえます。通常は剛体モード は結果評価の対象としません。
(図13)はAnsysで何も支持条件を設定せずに計算した ときの固有振動数の結果例です。並進3 方向と回転3 方向 がすべてフリーですので、合計6 個の剛体モードが検出さ れています。
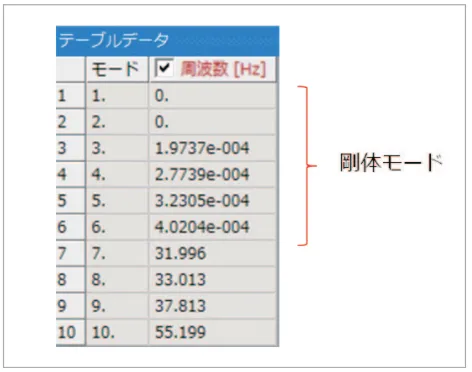
図13 剛体モードの検出例
7 Ansysモーダル解析事例
(図14)はAnsysで実施したブラケットのモーダル解析例です。ブラケットはシェル要素でモデル化しています。1次の固有振動数を上げることを目指し、対策前の1次モードの固有モードを参考にして、ブラケット周囲にリブをたて剛性を上げる変更を行って、効果を確認しています。
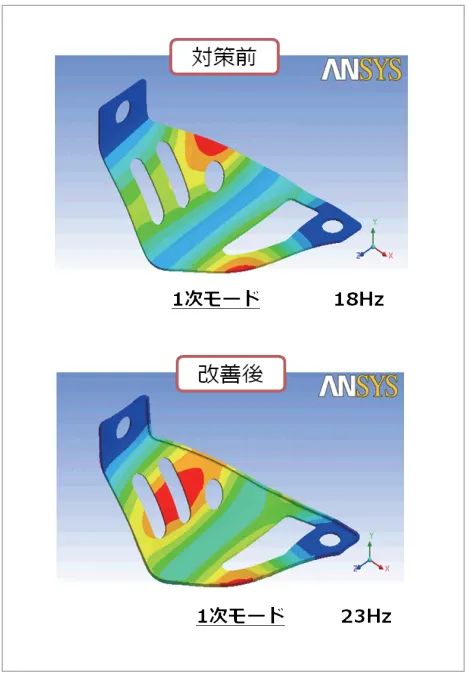
図14 ブラケットのモーダル解析例
8 (補足) 実固有値解析と複素固有値解析
9 おわりに
参考文献
[1] 一般社団法人 日本機械学会 計算力学技術者資格認定事業委員会
(https://www.jsme.or.jp/cee/)
[2] Ansysオンラインヘルプ > 構造解析ガイド > モーダル解析
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

コントローラ&センサのデータ駆動型シミュレーション
~データ駆動によるロボットのモデリングと制御設計~
-

EMCのお悩みありませんか? ~EMCソリューション~
-

炭素回収・利用・貯留におけるCO2の削減 ~Ansys Fluentによるソリューション~
~Ansys Fluentによるソリューション~
-

仮想環境で実現するマシンビジョン設計~Ansys Speosによるカメラ&照明最適化ソリューション~
~Ansys Speosによるカメラ&照明最適化ソリューション~
-
構想設計ですぐにリアルタイム検証 ~解析専任者ゼロでも使いこなせるAnsys Discovery~
~解析専任者ゼロでも使いこなせるAnsys Discovery~
-
流体機器設計の新たな一歩
~Ansys Discoveryで加速する設計改革~
-
筐体の冷却性能を構想設計から見える化 (手戻りを削減できる)
~Ansys Discoveryで始める電気筐体製品の設計改革~
-
若手でもすぐに使えるリアルタイム解析 (勘と経験からの脱却)
~Ansys Discoveryによる30名規模メーカーの設計改革~