CAEを学ぶ
モデル低次元化 (ROM) の基礎
1.モデル低次元化 (ROM) の基礎
1-1.モデル低次元化 (ROM) とは
始めにモデル低次元化 (ROM) について、解説をいたします。日本語ではモデル低次元化のことをモデル縮退(しゅくたい)や、モデル縮約(しゅくやく)といった名称で呼ばれることが多いようです。各専門分野によってその呼び方は異なるように見受けられます。英語ではReduced Order Modeling, 又はModel Order Reductionと呼ばれるようです。もともと、Model Order Reductionという用語は、筆者の知る限り制御理論の分野で開発された用語のようです。
制御理論の分野、特に現代制御理論における制御対象を微分方程式で表現し、動的な特性を研究する分野においては、制御対象の複雑さを軽減しながら、入出力の動作を可能な限り維持しようと努めることが多いと思います。
(制御理論に関するモデル低次元化にご興味がおありの方は、和書では参考文献[1]に挙げるものが詳説されております。) もともとは制御理論の分野から端を発したモデル低次元化(ここでは英語のModel Order reductionを指します)の理論ですが、近年では数値計算の研究等とも密接に関連して盛んに研究がされており、その守備範囲は制御の分野に限らず広がっているようです。
科学技術計算においては、まずその物理現象を常微分方程式や偏微分方程式で表現することが一般的ですが、微分方程式を実用に供する形で解くためにはコンピュータによる数値計算が欠かせません。特に偏微分方程式は、有限要素法や有限体積法などにより空間離散化された動的な多次元微分代数方程式へ変換されます。この微分代数方程式を解くために数値計算が大きな役割を担う訳ですが、一般に工学問題で扱う離散化された多次元微分方程式の次元は10^5から10^9程度(分野によってはそれ以上の規模)になり、最高性能のコンピュータや最新のアルゴリズムを用いても計算速度の向上には限界があることも事実です。そこにモデル低次元化は大きな役割を果たすことになると筆者は考えています。ここではもう少しモデル低次元化についてイメージを掴んでいただくために数学的な厳密な説明は経ずに例を用いて説明したいと思います。
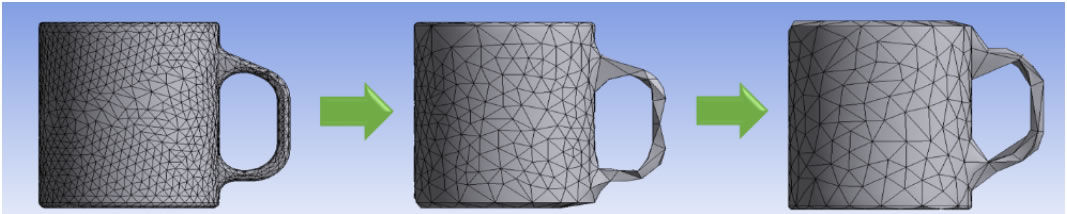 図1 モデル低次元化のイメージ図
図1 モデル低次元化のイメージ図上記の図1はマグカップをイメージしたコンピュータグラフィックスによる図です。この図は「マグカップであるということは少ない面から作られるグラフィックでも十分伝わる」ということを示しています。これは情報の少ないグラフィックでも、そのものの重要な特性は十分に伝わるということを示した例ですが、これを数学的、工学的な問題に置き換えたものが筆者の伝えたいモデル低次元化ということになります。モデル低次元化の理論的な内容については後述いたします。
1-2.何故モデル低次元化 (ROM) は必要なのか
前項においてモデル低次元化の概要について筆者の見識にて説明させていただきました。この節ではモデル低次元化が必要とされる背景や動機についてもう少し具体的な例を交えながら説明させて頂きます。(ここで挙げる例は主に参考文献[2]を参照しています)
筆者はモデル低次元化をまず純粋な数学的アルゴリズムの応用という観点から少し視点を広げて捉えてみたいと思います。ここではそれを“広義の意味でのモデル低次元化”と言いたいと思います。ここでいう“広義の意味でのモデル低次元化”とは、捉えようとする物理現象や工学的対象を俯瞰してみるのか、局所的に捉えるのか、またその現象をどのような数式(通常は微分方程式)で表現することが適切なのか、さらにモデル化したい対象を必要かつ十分に表現できているのかということであると申し上げたいと思います。このような観点から今日非常に成功していると考えられる例を一つ挙げれば、集積回路(LSI)設計の分野があげられるのではないかと思います。集積回路は、数百万(場合によってはそれ以上)の素子から構成されています。
一般に電子回路は抵抗、コンデンサ、インダクタ、ダイオード、トランジスタなどから構成されますが、トラジスタは抵抗や、コンデンサ、インダクタなどと比較するとその特性は極めて複雑で、それらの動作を正確にシミュレーションする場合には、専用の半導体デバイスシミュレーションによる計算を実施しなければなりません。半導体デバイスシミュレーションは通常有限要素法などの数値解析技術を用いて素子単独の動的な挙動を知ることになるのですが、数百万個あるトランジスタを含めた電子回路全体の完全なシミュレーションを半導体デバイスシミュレーションで実行することは事実上不可能です。このような場合、一般には半導体デバイスシミュレーションで計算し、取得した結果から何らかのモデル低次元化の技術を用いて電子回路シミュレーションで使用可能な単純化されたトランジスタモデルとして利用する必要があります。ここでは集積回路設計の例を挙げましたが全体を俯瞰して動的な挙動をシミュレーションする場合は電子回路シミュレーションによる方法を、またその中に現れるトランジスタの特性を素子として表現するには半導体デバイスシミュレーションによってミクロな挙動を把握し、その特性を電子回路のシミュレーションに取り込めるように様々な低次元化されたモデルとして表現されています。(この分野については参考文献[3]で詳説されています。)
さらに非常に面白い例としては人体の血流のモデルをユニークな視点でモデル低次元化を適用してシミュレーションする事例(参考文献[4])も報告されています。この論文では非常に小さな動脈は1次元のモデルで、やや大きい動脈は2次元のモデルで心臓は3次元のモデルで表現するといった方法で人体の血流をシミュレーションすることに成功している例です。先ほどの集積回路の例と同様に、人体全体の血流をシミュレーションするのに血管全体を3次元のモデルで表現することが適切ではないことを示すよい例となっています。ここで筆者が伝えたいことは、”広義の意味でのモデル低次元化”とは従来から研究者や技術者が行ってきた”モデル化”という行為の中に含まれるということです。(そのためこの意味では多くの皆さんがおそらく意識するかしないかに関わらず”広義の意味でのモデル低次元化”は既に行っているケースが多いのではないかと考えられます。) もう少しはっきり申し上げれば、適切にモデル化をする≒”広義の意味でのモデル低次元化”をするということになると考えられます。この“モデル化”と呼ばれる行為を適切に行うには、それを行おうとする人の経験や知見に深く依拠している場合が多く、“モデル化”の力を独力で身に着けていくことが難しいことも事実です。しかしながら分野(例えば集積回路設計のような分野)によっては体系化された方法論が存在したり、それらを知る人から教えを請うこともできるものと思いますので、ここでは敢えてどのように“広義の意味でのモデル低次元化”の経験や知見を深めればよいかということには立ち入らないことにしたいと思います。
次に視点を変えて、純粋な数学的アルゴリズムによるモデル低次元化の方法に目を向けたいと思います。ここでは先ほどの“広義の意味でのモデル低次元化”と概念を区別するために”狭義の意味でのモデル低次元化“と呼びたいと思います。その方法については後述することにして、それが求められる背景や動機についてまずは立ち入りたいと思います。先ほども申し上げた通りモデル低次元化の数学的方法論は主にシステム制御の分野から端を発したと申し上げました。そこには数値計算の理論(特に著者は線形代数の理論)が深く関連して発展してきたとみています。あまり馴染みのないものかもしれませんが数値計算の教科書に固有値を求めるアルゴリズムとしてランチョス法やアーノルディ法いう手法が紹介されることがしばしばあります。簡単に申し上げるとランチョス法は行列を三重対角行列に変換して固有値、固有ベクトルを求めるアルゴリズムです。またアーノルディ法も同様に大規模行列の固有値を次元が圧縮された行列の固有値で近似するためのアルゴリズムになります。
ここでは詳細に立ち入りませんが、これらのアルゴリズムはKrylov(クリロフ)部分空間法と呼ばれる理論の中で一般化されます。いずれのアルゴリズムも基本的にはシステム(行列)の特性(固有値、固有ベクトル)をそれよりも低次元化されたシステム(行列)の特性(固有値、固有ベクトル)で近似しようという考えに基づいているとみることができます。始めはシステム制御と数値計算の分野がお互いに影響を及ぼして発展してきたと筆者はみていますが、Krylov部分空間の理論は様々な分野に応用できるという点から、現在では非常に多くの分野で研究がされています。電子回路の分野で応用された例としては参考文献[5]を挙げておきたいと思います。この論文では電子回路のパデ(Pade)近似とKrylov部分空間法との関連について述べられています。最初は線形の動的システムの領域で研究がすすめられたモデル低次元化の理論ですが、現在では非線形の動的システムにもその領域を広げています。
Krylov部分空間法を応用した手法(参考文献[6])やPOD(固有直交分解)(参考文献[2])、DMD(動的モード分解)(参考文献[7])など、最新の理論も数多くあります。またそれらの適用が見込まれる分野もシステム制御や電子回路の分野以外に、気象予測(データ同化)、分子動力学、航空宇宙工学、振動/音響論、半導体素子の製造工程における化学蒸着などの流体力学の分野等、枚挙にいとまはありません。これらの分野において課題解決のためにモデル低次元化を適用しようとする試みは積極的に進められています(参考文献[8])。社会的な要請に科学技術計算が応えていくことの中の一つの手段として、”狭義の意味でのモデル低次元化“は重要な役割を担っているということができるのではないでしょうか。
2.モデル低次元化 (ROM) の方法
ここでは筆者の知る範囲でいわゆる“狭義の意味でのモデル低次元化”の代表的な方法を、いくつか紹介したいと思います。
2-1.モード縮退
2-1-1.モード縮退
モード縮退は主に振動問題でしばしば用いられる手法です。振動現象が低次の周波数に支配される場合には、高次の周波数を削除してモデルの次元を大幅に削減することができます。振動現象では高次になると減衰の効果が大きくなるので、低域側の特性が重要になることが多く、そのためモード縮退は非常に有効なモデル低次元化の手法の一つです。
ここではまず以下のような運動方程式を考えます。一般に有限要素法等で空間離散化されたモデルは大規模な次元(ここでは行列の次元をnとしておきます)を持つ以下のような集中定数系の常微分方程式になります。
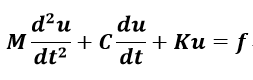 (1-1)
(1-1)上記の式(1-1)から減衰行列Cと外力項fをゼロとして以下の式を考えます。通常モード縮退は減衰項を考慮しない以下の二階の線形微分方程式に対して固有値問題を解きます。
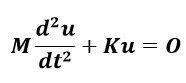 (1-2)
(1-2)上記の式(1-2)に対してuを以下のような周期関数を解として仮定します。
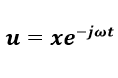 (1-3)
(1-3)式(1-3)を式(1-2)に代入して整理すると以下の式を導くことができます。
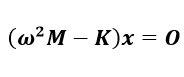 (1-4)
(1-4)上記の形式は、Ax=ΛBxの形を持つ一般固有値問題になります。式(1-4)に対してK -1 を左から乗じて、1/ω 2 =Λとおけば、
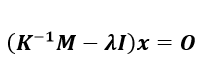 (1-5)
(1-5)となり、Ax=Λxの標準固有値問題に帰着します。ここでは式(1-4)の固有値問題を解いて得られる固有値と固有ベクトルを用いて式(1-1)の運動方程式を非連成化します。ここで固有ベクトルの列X r =[■(x 1 &…&x r )]を用いて、運動方程式の解を以下のように表現します。モード縮退では主に低域のモードが重要になるという点から高次のモードまでを求めることはしない為、元の運動方程式の次元からは大幅に低次元化されます。(r≪nとなります。)
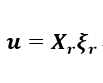 (1-6)
(1-6)ここで、ξ r はモード座標と呼ばれる変数になります。固有ベクトルとモード座標から運動方程式を以下のように現します。
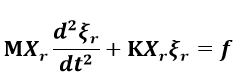 (1-7)
(1-7)更に式(1-7)の左からX r T (固有ベクトル列の転置)を掛けます。
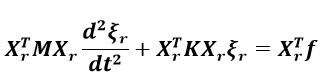 (1-8)
(1-8)ここで、先の一般固有値問題として表現された式(1-4)を解いて得られた固有ベクトルは(証明は省略いたしますが)直交性を持つことが知られており、式(1-8)の係数行列はそれぞれ以下のように表現することができます。
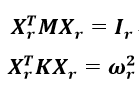 (1-9)
(1-9)式(1-9)を用いて式(1-8)を表現すれば、式(1-1)の運動方程式がモード座標による運動方程式に低次元化されたことになります。
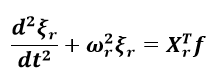 (1-10)
(1-10)マトリクスの成分毎に式(1-10)を記述すると以下のようになります。
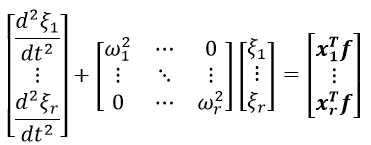 (1-11)
(1-11)モード縮退では、固有値問題で解いた固有ベクトルと式(1-11)を解いて得られたモード座標を掛け合わせて表現される式(1-6)が元の運動方程式の近似解になります。ここでは更にモード縮退で得られた(モード座標で現された)運動方程式を変数変換して状態空間実現で表現しなおしてみたいと思います。振動制御などの問題を扱う場合、モード座標の運動方程式を状態空間実現へ表現しなおすことで現代制御の理論を活用することができるようになります。またこの後にご紹介させていただくKrylov部分空間法とも関連する内容になりますので、ここでご紹介させていただきたいと思います。
2-1-2.状態空間実現
まずここでは前節で導出した式(1-10)のモード座標を次のように置き換えます。
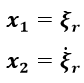 (1-12)
(1-12)ここで式(1-12)のξ r のドットは時間微分を表しています。( ξ r =(dξ r )/dtのことです。)
式(1-10)に式(1-12)の変数を代入すると、
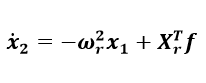 (1-13)
(1-13)となり、式(1-12)と式(1-13)を用いて表現すると以下のようになります。
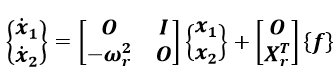 (1-14)
(1-14)さらに出力方程式の出力を以下のように変位とすると、
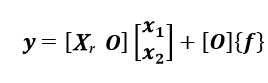 (1-15)
(1-15)上記のように現すことができて、式(1-14)と式(1-15)をまとめて以下のように記述したものを状態空間実現と呼びます。
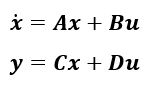 (1-16)
(1-16) ここで、 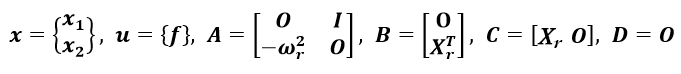 となります。状態空間実現のAをシステム行列、Bを入力行列、Cを出力行列、Dを直達行列とそれぞれ呼びます。
となります。状態空間実現のAをシステム行列、Bを入力行列、Cを出力行列、Dを直達行列とそれぞれ呼びます。
2-2.Krylov部分空間法
2-2-1.Krylov部分空間
ここではkrylov部分空間によるモデル低次元化とはどのようなものなのか、数学的な厳密性には少々目をつぶって頂いて説明を試みたいと思います。
ベクトルvに行列Aのべき乗を掛けて生成されるベクトル列v,Av,A 2 v,…のことをKrylov列といいます。最初のベクトルvから行列A をr-1回掛けたA (r-1) vまでのベクトルで張られる部分空間のことをr次Krylov 部分空間といい以下のように現します。
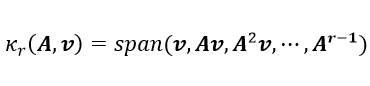 (2-1)
(2-1)ベクトル列のv,Av,A 2 v,…は部分空間の基底になるのですが、これらのベクトル列は行列Aを乗じていくだけでは各々が直交するわけではないのでGram-Schmidt(グラム-シュミット)の正規直交化法による直交化を行なう必要があります。その際には行列の対称性などを考慮してLancoz(ランチョス)法やArnoldi(アーノルディ)法といった様々なアルゴリズムの手法がとられます。またKrylov 部分空間による近似精度はベクトル列(基底)の数によって決まってきます。どの程度までベクトル列(基底)の数を取れば精度的に十分であるかといったご指摘もあるかと思いますが、精度を評価する指標もHankel(ハンケル)ノルム等を用いた方法が知られています。しかしながらここではその詳細については立ち入らないことにさせていただきます。これらに関する内容は参考文献[9]に詳しい紹介がありますのでご参考いただければと思います。また部分空間や基底という言葉の正確な定義につきましても線形代数等の書籍に詳しい記述がありますのでここではその詳細については割愛させていただきます。
ここに再び前節の最後にご紹介した状態空間実現を再度記述してみたいと思います。
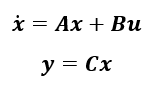 (2-2)
(2-2)ここでは直達行列Dはゼロ(D=O)としています。式(2-2)の状態空間実現の式を低次元化するためにKrylov部分空間法による基底を用いて、以下のように状態空間実現の解を表現することを考えてみます。
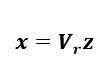 (2-3)
(2-3)式(2-3)のV r はKrylov部分空間法によって構成されたベクトル列 V r =[■(v 1 ,&…,&v r )]であることを想定しています。少し乱暴な言い方をすれば低次元化をするには何らかの方法で式(2-3)のような状態空間実現の解を表現することができればよいということになります。式(2-3)を式(2-2)へ代入して状態方程式の左側からV r T を掛けると以下のように表現することができます。(ここでは V r T V r =I(単位行列)となることを仮定しています。)
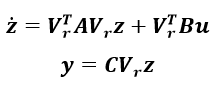 (2-4)
(2-4) ここで、 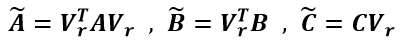
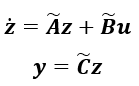 (2-5)
(2-5)式(2-2)が式(2-5)へ変換されて状態変数の次元は低次元化されました。(が状態空間実現として入出力の数は変わっていません。Krylov部分空間法による低次元化は制御理論における相似変換とみることもできます。) 少し前置きが長くなってしまいましたが、次に具体的にV r を求める方法としてArnoldi法によるアルゴリズムをご紹介したいと思います。式(2-2)の状態方程式を伝達関数表記しますと以下のようになります。
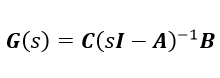 (2-6)
(2-6)天下り的な言い方で恐縮ですが、上記の式(2-6)で表現される伝達関数はArnoldi法などのアルゴリズムを適用することで行列AをKrylov部分空間に射影してAとすることができます。この辺りは伝達関数(のPade近似)とKrylov部分空間法との関係性についての証明を経る必要があるのですが、参考文献[9]に詳しい紹介がありますのでご参照いただければと思います。
Arnoldi法のアルゴリズムは次のようになります。
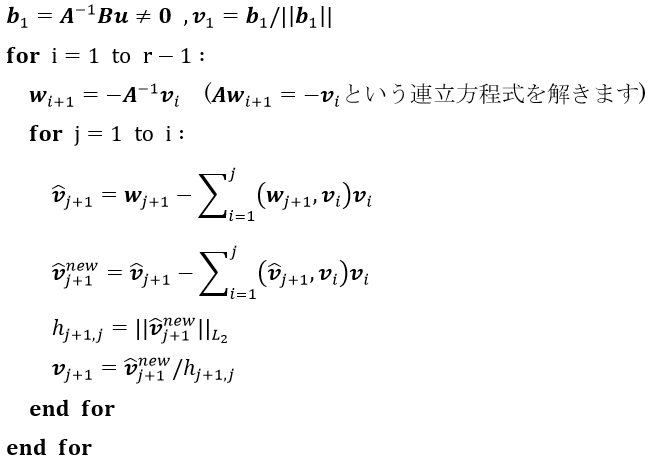 (2-7)
(2-7)上記のアルゴリズムで逐次求まるv (j+1) がKrylov列のV r になります。Krylov部分空間法のアルゴリズムは様々な手法が各分野で提案されておりまして、この分野の情報については参考文献[8]に詳しい紹介がございますのでご参考いただければと思います。ここでは、ほんの少しではありますがKrylov部分空間法に関する概要をご紹介させて頂きました。
2-3.固有直交分解(POD:Proper Orthogonal Decomposition)
2-3-1.固有直交分解
流体解析の分野を中心に積極的に適用がすすんでいる固有直交分解についてご紹介したいと思います。統計学の分野では主成分分析、信号処理の分野等ではKarhunen-Loeve(カルーネン-レーべ)展開とも呼ばれる手法です。
流体の流れ場を以下のような形式で表現することを考えてみたいと思います。
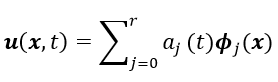 (3-1)
(3-1)ここで、u(x,t)は流れ場の速度ベクトル、a j (t)は展開係数、Φ j (x) は変動速度場のPOD基底と呼ばれるものになります。POD基底につきましては後述いたしたいと思います。以下の式は非圧縮性のNavier-Stokes(ナビエ-ストークス)方程式になりますが、
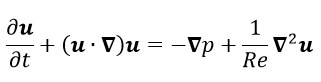 (3-2)
(3-2)この式(3-2)に式(3-1)を代入して、POD基底Φ i (x)との内積をとりますと式(3-2)のNavier-Stokes方程式は以下のように表現されます。
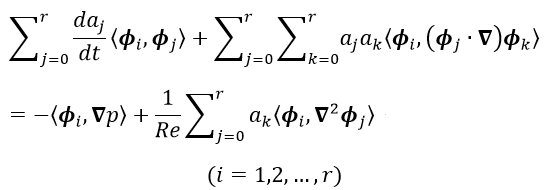 (3-3)
(3-3)証明は割愛させていただきますが上記の右辺第1項目は (Φ i ,∇p)=0 になります。参考文献14に記載がされておりますのでご参照いただけると幸いです。またPOD基底は互いに直交するため(Φ i ,Φ j )=δ i jとなります。ここでδ i jはクロネッカーのデルタです。式(3-3)を整理して書くと以下のように表現することができます。
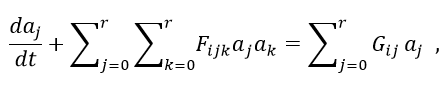 (3-4)
(3-4)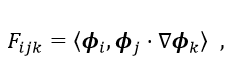 (3-5)
(3-5)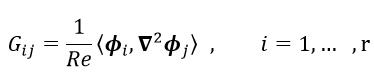 (3-6)
(3-6)上記の式(3-4)は非圧縮性のNavier-Stokes方程式をPOD基底によって低次元化した非線形常微分方程式になります。ここでF i jkとG i jはPOD基底が分かれば事前に計算しておくことができます。
さて、式(3-2)から式(3-4)を導出するためにはどうしても、このPOD基底と呼ばれるものを事前に取得しておく必要があります。POD基底自体は、前項で現れたKrylov部分空間の基底や、前々項のモード縮退で現れた固有ベクトルと非常によく似た概念です。大きな特徴としては非圧縮性のNavier-Stokes方程式のような非線形の偏微分方程式に対してもモデル低次元化が適用できてしまうところです。ここでは理論的な詳細には立ち入ることはできませんが具体的にはどのようにPOD基底を求めればよいかということを、次にご紹介していきたいと思います。簡単に概要を申し上げると流れのデータ(シミュレーションの結果データ)から行列を作成して、その固有値問題を求めて固有モードを求めます。この固有モードがPOD基底になります。その行列は以下のようなベクトル列Xから作ることができます。
 (3-7)
(3-7)ここで式(3-7)のXは、例えばCFD解析の各時刻での各格子点の流れ場の結果等のデータになります。またXは3n行m列の行列になっています。この行列Xを使って以下のような固有値問題を考えます。
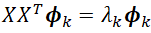 (3-8)
(3-8)ここで、λ k は固有値、Φ k は固有モードです。ここで低次元モデルを構築するのに、固有モードをいくつまで求めればよいかということを判断するのに、以下の公式が役に立ちます。
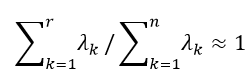 (3-9)
(3-9)ここで∑ (k=1) n λ k =tr([XX] T )となります。低次元モデルの近似精度をよくするには、式(3-9)が、1に近い値となるまでモードを取得するということになります。ここで式(3-8)の固有値問題を考えた場合、行列[XX] T はCFDのモデルの格子の数の3倍の行列になっています。3n×3nの行列となっています。さらに結果から取得したものを掛け合わせて作成しているので行列の成分をすべて持つ行列になっています。このため実際には、式(3-8) の固有値問題をそのまま解くということは一般には致しません。
そこでsnapshot PODと呼ばれる手法を用いて、式(3-8)の固有値問題を以下のような形式に変換して元の大規模な固有値問題を解くのではなく、等価な小規模な固有値問題を解いて固有値と固有モードを求めます。
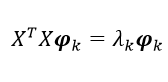 (3-10)
(3-10)ここで、行列X T Xは時間刻み分の次元になります。つまりm×mの行列になっています。詳しい証明は割愛させていただきますが、式(3-10)の固有値問題を解いて以下の式のように式(3-8)の固有モードを表現します。
 (3-11)
(3-11)式(3-11)のΦ k を用いることで式(3-5)のF i jk , 式(3-6)のG i jを求めることができます。その上で式(3-4)の低次元化されたモデルを構築することができるようになります。この節では固有直交展開についてご紹介をさせていただきましたが、ご興味のある方は巻末に挙げた参考文献などにあたって頂ければ大変幸いです。
3.最後に
近年のモデル低次元化の理論の中に大変興味深いものも多くありますが、今回はご紹介できなかったものなども多くございます。動的モード分解(DMD)やニューラルネットワークを用いた手法、Krylov部分空間法を二次双線形の問題へ適用している例など大変興味深い手法が多くあります。これらの手法につきましては巻末に挙げる参考文献を参照いただければ幸いでございます。
4.参考文献
[1].制御システム設計 コントローラの低次元化- システム制御情報学会編 大日方五郎 B.アンダーソン著
[2]. Wilhelmus H.A.Schilders, etc, Model Order Reduction, Springer
[3].Sheldon Tan, Lei He, Advanced Model Order Reduction Techniques in VLSI design, Cambridge University Press
[4].A. Quarteroni and A. Veneziani. Analysis of a geometrical multiscale model based on the coupling of PDE’s and ODE’s for blood flow simulations. SIAM J. on MMS,1(2): 173-195, 2003.
[5]. P. Feldmann and R. Freund. Efficient linear circuit analysis by Pad´e approximation via the Lanczos process. IEEE Trans. Computer-Aided Design, 14:137-158, 1993.
[6].W.Keiper,A.Milde, S.Volkwein, Reduced-Order Modeling (ROM) for Simulation and Optimization, Springer
[7]. J. Nathan Kutz , Steven L. Brunton, Bingni W. Brunton, Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems
[8].Athanasios C.Antoulas, Approximation of Large-Scale Dynamical System, SIAM
[9].T.Bechtold, etc, Fast Simulation of Electro-Thermal MEMS, Springer
[10]. 平邦彦, 固有直交分解による流体解析1.基礎,ながれ, 30, pp.115-123, 2011.
[11]. 平邦彦, 固有直交分解による流体解析2.応用,ながれ,30,pp.263-271, 2011
5.モデル低次元化 (ROM) の活用例のご紹介
以下のURLではモデル低次元化(ROM)の方法を、ツールを通じて実践していただき、システムシミュレーションに活用する具体的な方法を紹介しています。
CADFEM Ansys Extensionsのご紹介
【オンデマンド動画】ROMモデル作成用の「Model Reduction inside Ansys」その他についてご紹介します。
ROM (モデル低次元化) の概要
【資料ダウンロード】本資料ではROMについて数学的観点からご説明いたします。またCADFEM Ansys Extensions -Model Reduction inside Ansysを活用することで、Ansysの解析モデルをシステムレベルの解析に導入することが可能になります。
ROM化によるパワー半導体デバイスの効率的な電気-伝熱シミュレーション
【資料ダウンロード】資料では、モデル低次元化の最新数学的アルゴリズムに基づく効率的な方法論を提案し、パワーMOSFETモデルでのアプローチを示します。
熱回路網法とROM技術を 組み合わせた熱設計のご提案
【資料ダウンロード】 Ansysは、従来のMBDを大きく進化させた、新しいMBDソリューションを展開しております。システム全体(物理、電気、制御)をカバーするマルチランゲージおよび、3D のマルチフィジックスソリューションを縮退化する ROM 機能を備え、完全なシステムモデルの構築をめざしております。本資料では AnsysのMBDについてについて説明しています。
Ansys Twin Builder モデル低次元化によるマルチドメイン1Dシミュレーション事例
【資料ダウンロード】 Ansysは、従来のMBDを大きく進化させた、新しいMBDソリューションを展開しております。システム全体(物理、電気、制御)をカバーするマルチランゲージおよび、3D のマルチフィジックスソリューションを縮退化する ROM 機能を備え、完全なシステムモデルの構築をめざしております。本資料では AnsysのMBDについてについて説明しています。
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

実測 × 解析で基板の熱変形問題を解決!基板反り現象の高精度シミュレーション
~エスペック(株)×サイバネットシステム(株)の連携ソリューション~
-

【全記事】CAEのあるものづくり vol.42
ユーザー様インタビュー記事7件を1冊に集約した保存版
-

誤差との上手なつきあい方 ~流体解析の計算誤差~ (完全保存版)
誤差との上手なつきあい方 前編・後編 を1冊にまとめた保存版 PDF
-

非線形解析の最大強度評価はAnsys LS-DYNAで解決!
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析で電子機器の信頼性向上
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

共振回避だけで終わらせない振動解析の進め方を解説(周波数応答・時刻歴まで)
~Ansys Mechanicalで実現する高度な製品開発~