CAEを学ぶ
弾塑性材料モデルの基礎(第3回)
佐賀大学 大学院工学系研究科 機械システム工学専攻 只野 裕一 様
弾塑性材料モデルの基礎(第3回)の概要

弾塑性材料モデルの基礎 第1~4回 完全保存版 PDF を "無料" 公開中!

弾塑性材料モデルの基礎 完全保存版 PDF サンプル
これさえ読めば”弾塑性材料モデルの基礎”がわかる
全4回のシリーズとなっております「弾塑性材料モデルの基礎」について、4回分の解析講座を1冊でお読みいただける完全保存版 PDF を公開いたしました。どなたでも簡単なフォーム入力のみでダウンロードいただけますので、是非この機会にご利用ください。
ページ数:24 ページ
ファイル形式: PDF
佐賀大学 大学院工学系研究科
機械システム工学専攻 只野 裕一 様 著
【完全保存版 PDF 目次】
|
1. はじめに 2. 弾塑性モデルの概要 3. 弾塑性モデルを理解するための 予備知識 4. 降伏関数 |
5.ひずみ硬化則 6. 弾塑性構成式の基礎 7. おわりに |
5 ひずみ硬化則
5.1 ひずみ硬化則とは
前回は、材料の降伏条件について説明しました。降伏条件を記述する降伏関数が応力の関数となっていることからもわかるように、材料に作用する応力がある条件を満たしたとき、材料は降伏すると考えます。材料が弾性状態から塑性状態にはじめて遷移する瞬間を、特に初期降伏と呼ぶこともあります。今回は、初期降伏した後の塑性変形進行中に、材料の応力状態がどのように変化していくかを考えてみましょう。
材料がある応力状態で初期降伏した後、多くの材料においては塑性変形の進行と共に応力が増加していきます(第1回の図1)。これをひずみ硬化と呼びます。このひずみ硬化を表現するためのモデルが、ひずみ硬化則です。金属材料の多くは、塑性変形の進行とともにひずみ硬化を示しますが、一部の樹脂材料や、微視的損傷を考慮した金属材料の塑性変形においては、塑性変形が進行しているにもかかわらず応力が減少することがあり、これをひずみ軟化と呼びます。ひずみ軟化を表すモデルを、特にひずみ軟化則と呼ぶ場合もありますが、ひずみ硬化とひずみ軟化は基本的には同じように考えることができます。実際の材料のひずみ硬化挙動は、材料によって大きく異なります。このため、塑性変形をCAEで高精度に表現するためには、ひずみ硬化則の適切な選択とパラメータ同定が重要となります。
第2回で降伏関数について解説した際、塑性変形中は常に![]() となるようにモデル化することが一般的と述べました。これは、降伏応力が塑性変形の進行とともに変化することを意味しています。ひずみ硬化則は、この降伏応力の変化を表現するモデルといえます。ひずみ硬化則を考えるにあたっては、スカラー量である相当応力と相当塑性ひずみの関係を記述するモデルと、降伏曲面が塑性変形とともにどのように変化していくかを記述するモデルの、2つのモデルをそれぞれ考える必要があります。今回は、このうち相当応力と相当塑性ひずみの関係について見ていきましょう。
となるようにモデル化することが一般的と述べました。これは、降伏応力が塑性変形の進行とともに変化することを意味しています。ひずみ硬化則は、この降伏応力の変化を表現するモデルといえます。ひずみ硬化則を考えるにあたっては、スカラー量である相当応力と相当塑性ひずみの関係を記述するモデルと、降伏曲面が塑性変形とともにどのように変化していくかを記述するモデルの、2つのモデルをそれぞれ考える必要があります。今回は、このうち相当応力と相当塑性ひずみの関係について見ていきましょう。
5.2 1次元問題における相当応力と相当塑性ひずみ
第2回で紹介したように、テンソル量である応力からスカラー量であるMisesの相当応力を定義することで、Misesの降伏条件をスカラー関数として表現することができます。すなわち、相当応力とは本来3 次元的な応力状態は、1次元的なスカラーで表現可能な量といえます。より複雑な降伏関数の定義においても一般に相当応力を定義することができますので、以下の解説における相当応力は、Misesの相当応力を含めた一般的な相当応力と考えます。
また、単軸引張のような1 次元的な応力状態であれば、軸方向応力がそのまま相当応力に対応します。相当塑性ひずみの詳細な定義については第4回で取り上げますので、今回は1次元的な場合についてのみ考えておきましょう。弾塑性問題においては、一般に変形を弾性変形と塑性変形に分解することを考えます。この分解にはいくつかの方法がありますが、最も簡単なアイデアは、ひずみが弾性成分と塑性成分の和で表せるという加算分解の考え方です。すなわち、1次元問題で軸方向のひずみを![]() としたとき、次式が成立すると考えます。
としたとき、次式が成立すると考えます。

ここで、![]() と
と![]() をそれぞれ弾性ひずみ、塑性ひずみと呼びます。このうち、弾性ひずみに対しては弾性構成則が成り立つと仮定するのが一般的で、1次元問題であれば軸方向応力を
をそれぞれ弾性ひずみ、塑性ひずみと呼びます。このうち、弾性ひずみに対しては弾性構成則が成り立つと仮定するのが一般的で、1次元問題であれば軸方向応力を![]() 、ヤング率を
、ヤング率を![]() として
として![]() の関係を仮定します。これより、
の関係を仮定します。これより、

となりますから、式(2)を式(1)に代入することで
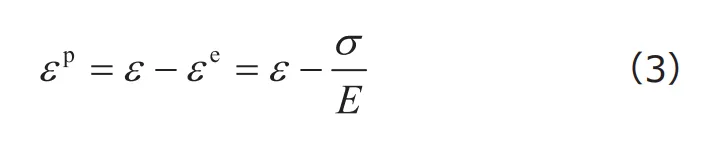
が得られます。単軸引張試験を実験的に行うことで、軸方向応力![]() と
と![]() 軸方向ひずみ が実測できますから、ヤング率が既知であれば軸方向の塑性ひずみを算出することができます。そして相当応力と同様に、1次元問題では軸方向塑性ひずみが相当塑性ひずみと等しくなります。すなわち、単軸引張試験を行うことで、相当応力と相当塑性ひずみの関係を測定することができます。
軸方向ひずみ が実測できますから、ヤング率が既知であれば軸方向の塑性ひずみを算出することができます。そして相当応力と同様に、1次元問題では軸方向塑性ひずみが相当塑性ひずみと等しくなります。すなわち、単軸引張試験を行うことで、相当応力と相当塑性ひずみの関係を測定することができます。
5.3 相当応力と相当塑性ひずみの関係を表すひずみ硬化則
相当応力と相当塑性ひずみの関係を表すひずみ硬化則について、いくつかの具体例を見ていきましょう。前節では1 次元的な場合の相当応力と相当塑性ひずみについて述べましたが、本節で扱うひずみ硬化則は一般的な3次元状態に対しても適用することが可能です。
ここでは、主に金属で用いられる4つのひずみ硬化則を紹介します。なお、ひずみ硬化則は一般に相当塑性ひずみの関数となることから、本稿ではこれを![]() と表すことにします。より複雑なひずみ硬化挙動を表現する際には、
と表すことにします。より複雑なひずみ硬化挙動を表現する際には、![]() が相当塑性ひずみ以外の状態量(例えば温度や変形速度など)も引数として持つことになります。第2回で述べたように、降伏関数は一般に塑性変形中は常に
が相当塑性ひずみ以外の状態量(例えば温度や変形速度など)も引数として持つことになります。第2回で述べたように、降伏関数は一般に塑性変形中は常に![]() となるようにモデル化しますが、これは塑性変形と共に降伏応力が変化していく(ひずみ硬化であれば応力が上昇していく)ことを意味しています。このとき、塑性変形中のある瞬間における降伏応力が
となるようにモデル化しますが、これは塑性変形と共に降伏応力が変化していく(ひずみ硬化であれば応力が上昇していく)ことを意味しています。このとき、塑性変形中のある瞬間における降伏応力が![]() であると考えられます。すなわち、ここで解説するひずみ硬化則は、塑性変形に伴う降伏応力の発展則といえます。
であると考えられます。すなわち、ここで解説するひずみ硬化則は、塑性変形に伴う降伏応力の発展則といえます。
5.3.1 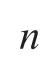 乗硬化則
乗硬化則
金属材料では一般に、初期降伏後の応力の増加率(応力・ひずみ線図の傾き)は、塑性変形の進行とともに小さくなります。これを表現するために、べき乗形の関数を用いたひずみ硬化則がよく用いられます。その一つである「![]() 乗硬化則」もしくは「べき乗硬化則」と呼ばれるひずみ硬化則は、次式で表されます。
乗硬化則」もしくは「べき乗硬化則」と呼ばれるひずみ硬化則は、次式で表されます。
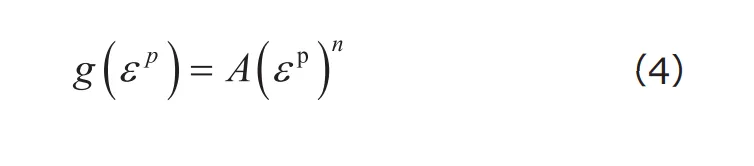
相当応力が相当塑性ひずみの![]() 乗の関数となることから、この名が付いています。ここでは
乗の関数となることから、この名が付いています。ここでは![]() と
と![]() の2つが材料定数となり、これらを実験と整合するよう決定することになります。また、
の2つが材料定数となり、これらを実験と整合するよう決定することになります。また、![]() は一般に
は一般に![]() の値をとります。
の値をとります。
このひずみ硬化則によって得られる相当応力・相当塑性ひずみ関係を、図1に例示しています。また、2つの材料定数![]() と
と![]() を変化させたときの、相当応力・相当塑性ひずみ関係への影響を図2に示します。図1、2からもわかるように、
を変化させたときの、相当応力・相当塑性ひずみ関係への影響を図2に示します。図1、2からもわかるように、![]() 乗硬化則では塑性変形は相当応力がゼロの状態から開始します。相当応力がゼロの状態から開始するということは、初期降伏応力がゼロであることを意味しており、これは純粋な弾性変形状態が存在しない、すなわち変形の初期段階から塑性変形が進行していることを表します。
乗硬化則では塑性変形は相当応力がゼロの状態から開始します。相当応力がゼロの状態から開始するということは、初期降伏応力がゼロであることを意味しており、これは純粋な弾性変形状態が存在しない、すなわち変形の初期段階から塑性変形が進行していることを表します。
5.3.2 Ludwik 硬化則
現実の弾塑性挙動では、変形初期は弾性状態であり、相当応力が初期降伏応力に達したときに塑性変形が開始しますから、上記の![]() 乗硬化則は現実的な弾塑性挙動を表現するには、少々具体が悪いことになります。そこで、次式で定義される「Ludwik硬化則」が提案されています。
乗硬化則は現実的な弾塑性挙動を表現するには、少々具体が悪いことになります。そこで、次式で定義される「Ludwik硬化則」が提案されています。
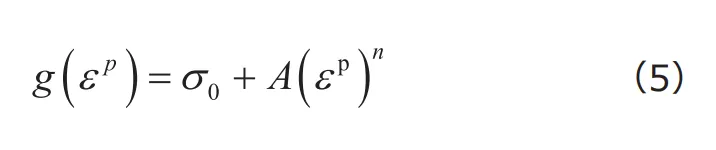
これは![]() 乗硬化則に定数
乗硬化則に定数![]() を加えた形となっており、
を加えた形となっており、![]() は初期降伏応力に対応する材料定数となります。Ludwik硬化則の模式図を図3に示します。相当塑性ひずみがゼロのときの相当応力がゼロではなく
は初期降伏応力に対応する材料定数となります。Ludwik硬化則の模式図を図3に示します。相当塑性ひずみがゼロのときの相当応力がゼロではなく![]() となっており、より現実的なひずみ硬化則となっています。
となっており、より現実的なひずみ硬化則となっています。![]() を変化させたときの、ひずみ硬化則への影響を図4に表しています。グラフの形はそのままに、
を変化させたときの、ひずみ硬化則への影響を図4に表しています。グラフの形はそのままに、![]() の分だけ応力が上下に平行移動することがわかります。また材料定数
の分だけ応力が上下に平行移動することがわかります。また材料定数![]() と
と![]() の働きは、
の働きは、![]() 乗硬化則と同じです。
乗硬化則と同じです。
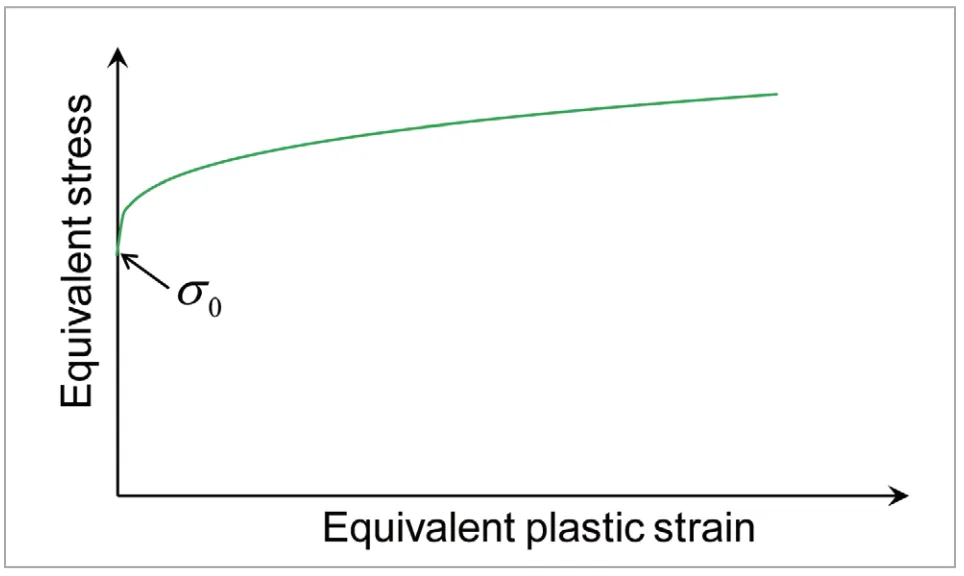
図3 Ludwik硬化則
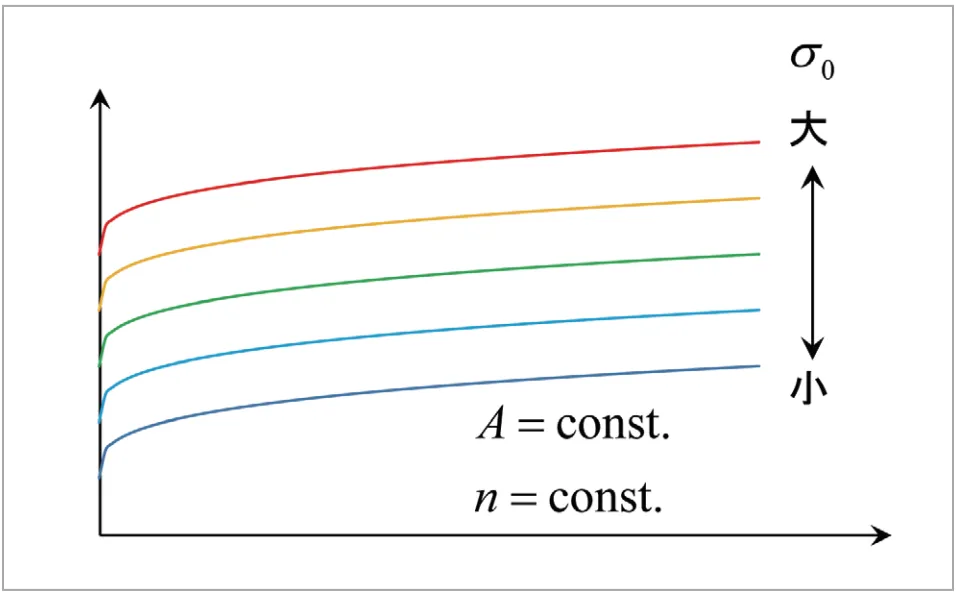
図4 Ludwik硬化則における材料定数の影響
5.3.3 Swift 硬化則
べき乗の形式をとるもう一つの硬化則として、「Swift硬化則」が知られています。これは、次式で与えられるひずみ硬化則です。
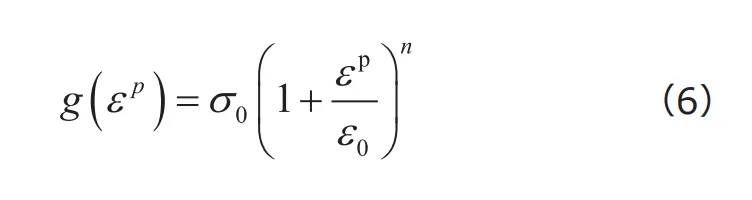
![]() 乗硬化則やLudwik硬化則同様、指数
乗硬化則やLudwik硬化則同様、指数![]() によって硬化則が特徴付けられていますが、式の形式が異なっており、
によって硬化則が特徴付けられていますが、式の形式が異なっており、![]() のほかに
のほかに![]() と
と![]() が材料定数となっています。
が材料定数となっています。 ![]() はLudwik硬化則と同じように、初期降伏応力に相当します。Swift硬化則の模式図を図5に示します。相当塑性ひずみがゼロのときの相当応力が
はLudwik硬化則と同じように、初期降伏応力に相当します。Swift硬化則の模式図を図5に示します。相当塑性ひずみがゼロのときの相当応力が![]() となっていることが確認できます。Swift硬化則における各パラメータを変化させたときの、ひずみ硬化則への影響を図6に表しています。3つのパラメータを変化させることで、それぞれグラフの形を変化させることができます。なお、このSwift硬化則のことを指して、単にべき乗硬化則と呼ぶ場合もあります。実際の金属材料に対して、実験データをSwift硬化則でフィッティングすることも多く、このとき
となっていることが確認できます。Swift硬化則における各パラメータを変化させたときの、ひずみ硬化則への影響を図6に表しています。3つのパラメータを変化させることで、それぞれグラフの形を変化させることができます。なお、このSwift硬化則のことを指して、単にべき乗硬化則と呼ぶ場合もあります。実際の金属材料に対して、実験データをSwift硬化則でフィッティングすることも多く、このとき![]() の値(
の値(![]() 値とも呼ばれます)の大小が塑性加工における加工性に強い影響を与えることから、特に重要なパラメータであることが知られています。
値とも呼ばれます)の大小が塑性加工における加工性に強い影響を与えることから、特に重要なパラメータであることが知られています。
図6からもわかるように、![]() 値が小さいと、相当塑性ひずみの増加とともに相当応力の増加率が低くなり、ひずみ硬化の程度が小さくなります。逆に
値が小さいと、相当塑性ひずみの増加とともに相当応力の増加率が低くなり、ひずみ硬化の程度が小さくなります。逆に![]() 値が大きいと、相当塑性ひずみが増加しても相当応力の増加率はあまり低下しません。すなわち、
値が大きいと、相当塑性ひずみが増加しても相当応力の増加率はあまり低下しません。すなわち、![]() 値が大きいということは、初期降伏後のひずみ硬化の度合いが高いことを表しています。
値が大きいということは、初期降伏後のひずみ硬化の度合いが高いことを表しています。
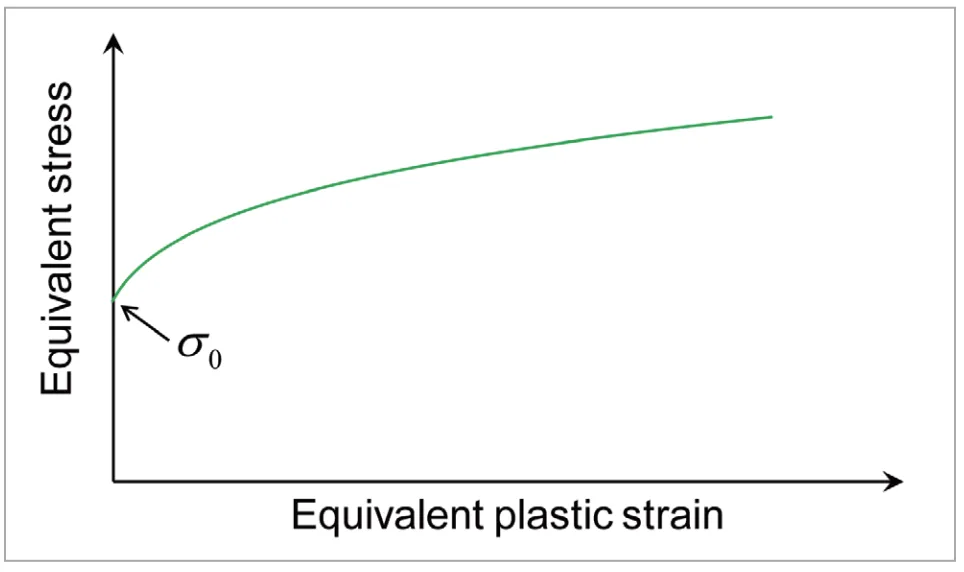
図5 Swift硬化則
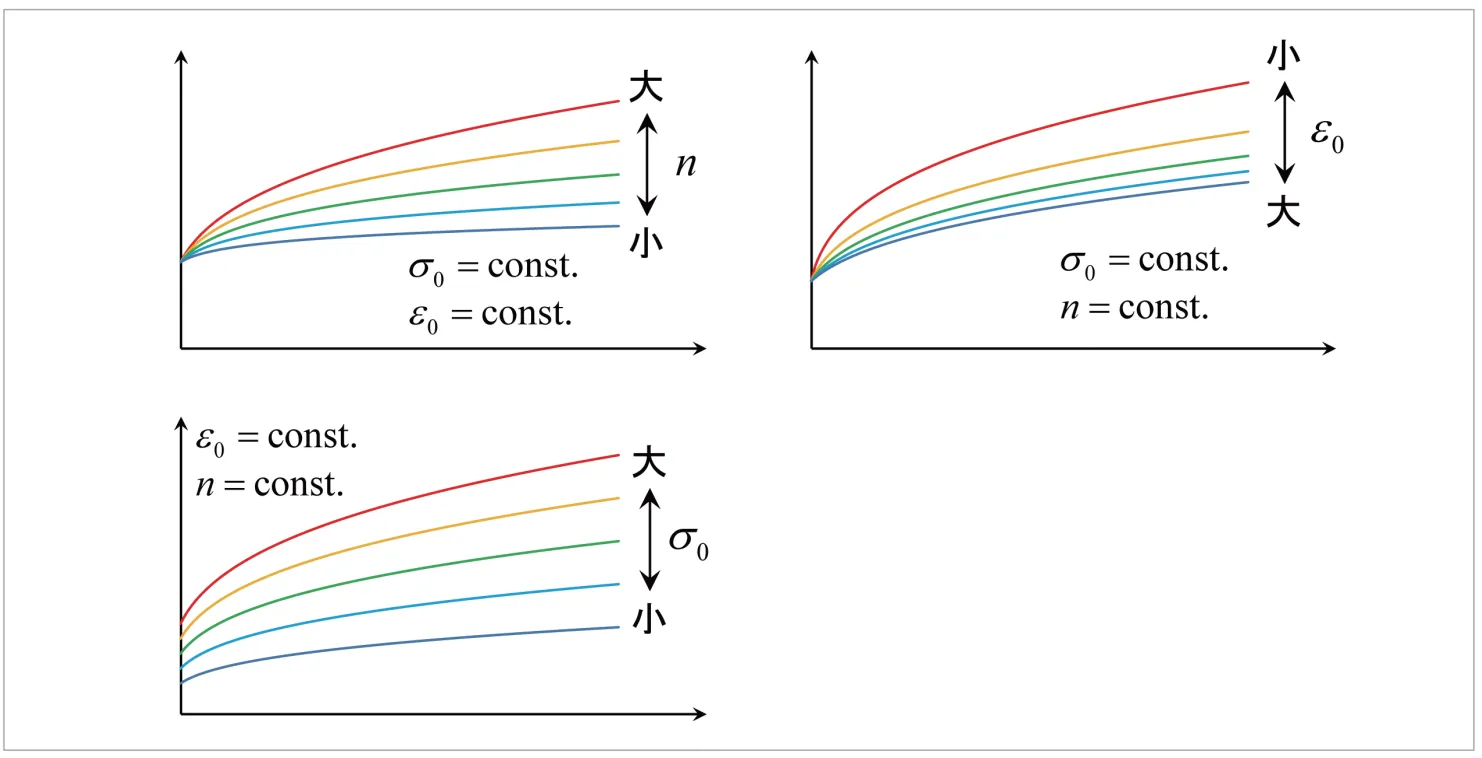
図6 Swift硬化則における材料定数の影響
5.3.4 Voce 硬化則
以上の3つのひずみ硬化則はいずれもべき乗形で表され、塑性変形の進行と共にグラフの傾きは小さくなるものの、相当応力はどこまでも単調増加する関数となっていました。べき乗形のひずみ硬化則は、多くの金属材料のひずみ硬化挙動に対応しますが、一部の金属材料では、塑性変形の進行とともに相当応力がある一定応力に収束するひずみ硬化挙動を示すものもあります。これを表現するひずみ硬化則として、「Voce硬化則」が知られています。Voce硬化則は次式で与えられます。
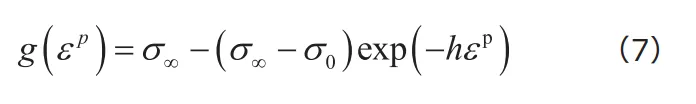
このひずみ硬化則では、![]() 、
、![]() 、
、![]() の3つが材料定数となります。
の3つが材料定数となります。![]() は初期降伏応力、
は初期降伏応力、![]() が最終的に収束する応力(飽和応力)にそれぞれ対応します。Voce硬化則の模式図を図7に、材料定数
が最終的に収束する応力(飽和応力)にそれぞれ対応します。Voce硬化則の模式図を図7に、材料定数![]() の影響を図8にそれぞれ示します。
の影響を図8にそれぞれ示します。![]() の値によって、飽和応力への収束の速さが変わることがわかります。
の値によって、飽和応力への収束の速さが変わることがわかります。
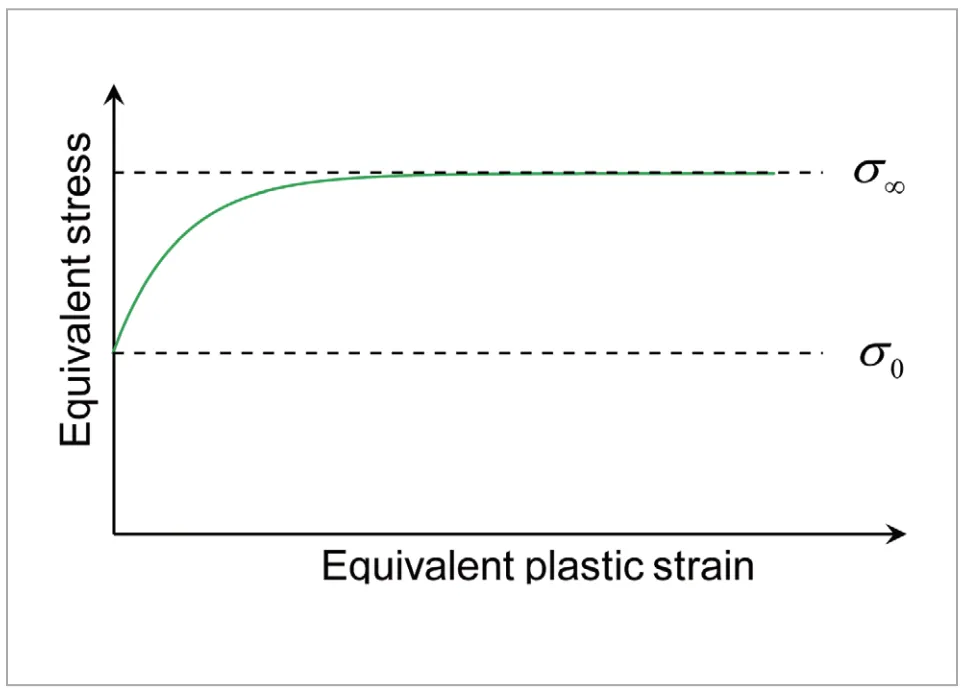
図7 Voce硬化則
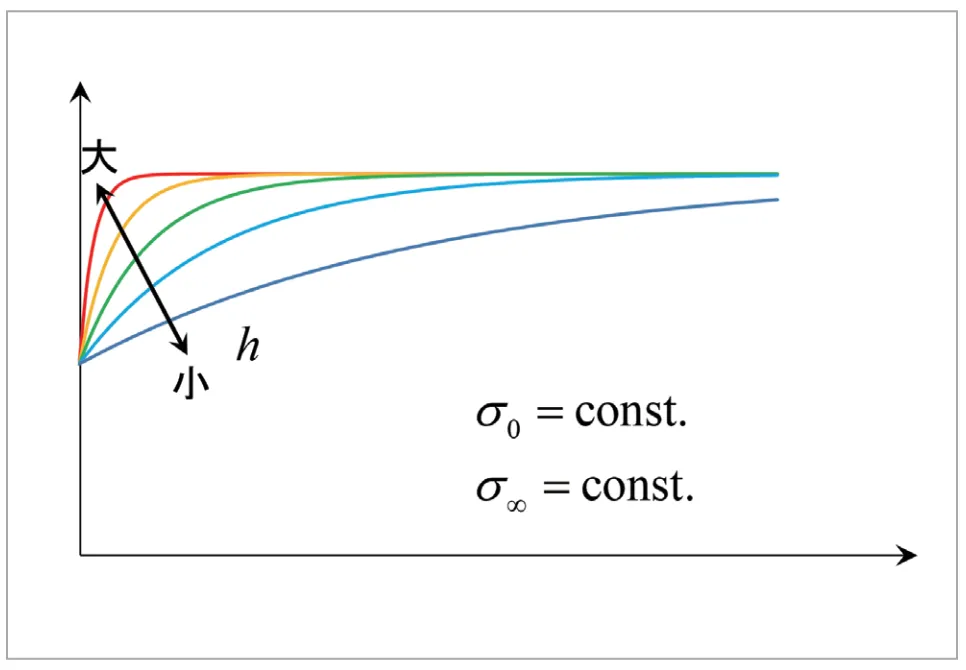
図8 Voce硬化則における材料定数の影響
5.3.5 多直線近似によるひずみ硬化則の表現
以上に、金属材料で主に用いられる4 つのひずみ硬化則を紹介しました。代表的な金属材料であれば、これらのひずみ硬化則が良好な近似となる場合も多いのですが、一方で樹脂材料などではより複雑なひずみ硬化挙動を示す場合もあります。例えば、ある種の樹脂材料は初期降伏後、しばらくひずみ硬化を示した後、一旦ひずみ軟化に転じ、さらに再度ひずみ硬化するという挙動を示します。このようなひずみ硬化挙動に対して、一般式を立てるのは困難です。また、一般式で表現できるひずみ硬化挙動であっても、材料パラメータを同定するのには少なくない手間がかかります。
そこで実際のCAEソフトウェアにおいては、ひずみ硬化則をこれらの数式ではなく多直線近似を用いたデータで入力することが多くなっています。入力データとして、相当応力と相当塑性ひずみのデータテーブルを与えることで、ひずみ硬化則を表現するわけです。これにより、パラメータ同定をすることなく、5.2 節で示したような単軸引張試験で得られるデータを直接入力とすることが可能となります。また、一般式を立てることが難しいひずみ硬化挙動でも、容易にひずみ硬化則を定義することができます。多直線近似の例として、Swift硬化則とVoce硬化則を多直線近似で表した例を図9に示します。ある程度の数の点を定義すれば、多直線近似でも十分であることがわかるかと思います。なお、与えるデータテーブルは、通常、等間隔なプロットである必要はありません。図9の例にもあるように、 傾きの変化が急激なところは点を多くし、変化が緩やかなところは少ない点で表現することで、最小限のデータ数でも十分なひずみ硬化則の近似が可能となります。
第3回は、初期降伏後にひずみ硬化挙動を表現するモデルとして、相当応力と相当塑性ひずみの関係を表すひずみ硬化則を解説しました。これを用いることで、塑性変形の進行に伴う降伏応力の変化を表現することができますが、3次元的な応力状態に対しては、これに加えて降伏曲面がどのように変化するかを定義する必要があります。第4回では、この降伏曲面の変化を表現するための硬化則について解説するとともに、弾塑性解析における応力と塑性ひずみの関係を表す構成式の基礎についてもご紹介します。
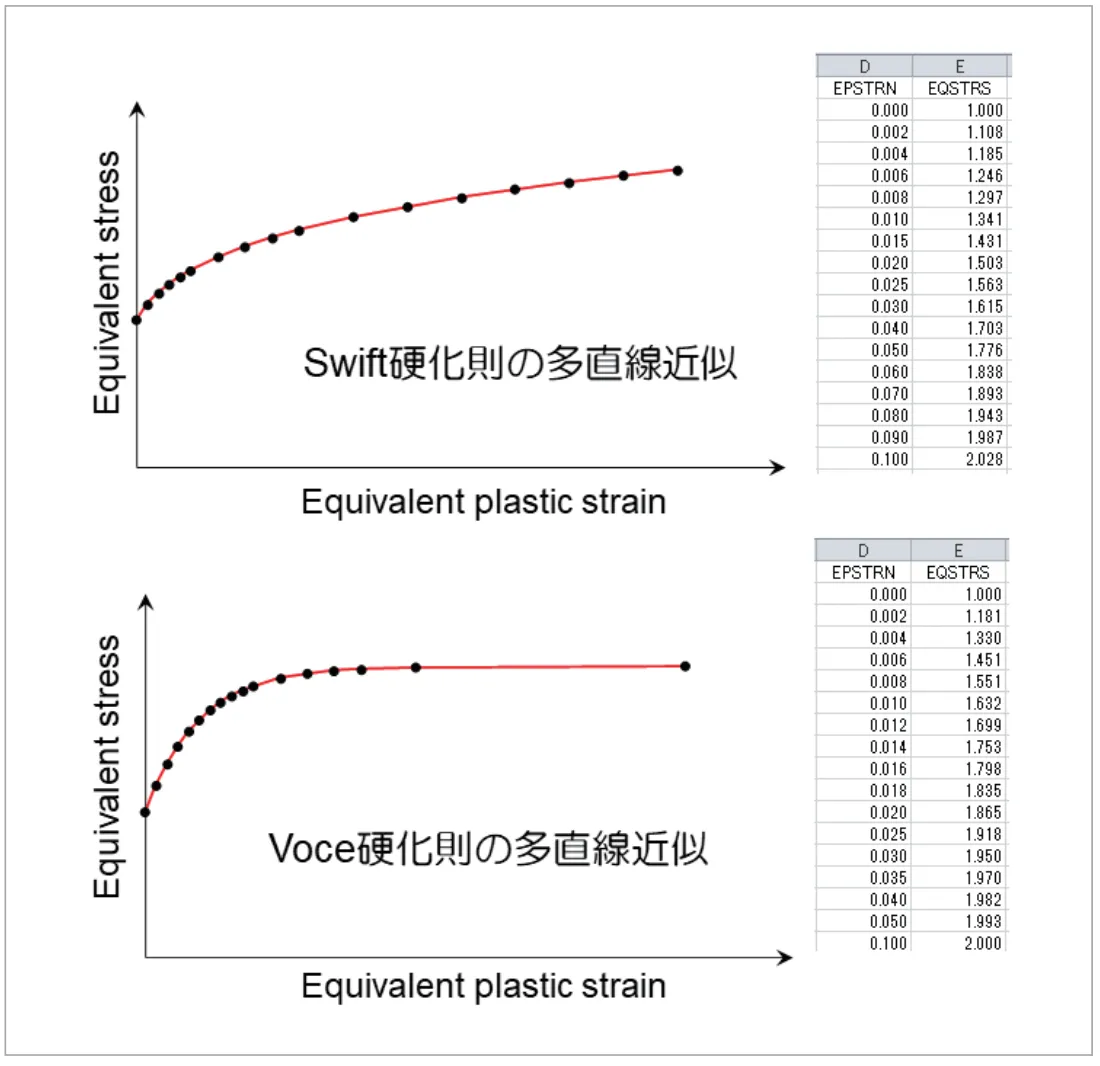
図9 多直線近似によるひずみ硬化則の表現
お問い合わせ
メカニカルCAE事業部 営業部
E-mail: anssales@cybernet.co.jp
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

【全記事】CAEのあるものづくり vol.42
ユーザー様インタビュー記事7件を1冊に集約した保存版
-

誤差との上手なつきあい方 ~流体解析の計算誤差~ (完全保存版)
誤差との上手なつきあい方 前編・後編 を1冊にまとめた保存版 PDF
-

非線形解析の壁を突破するシミュレーション技術
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

共振回避だけで終わらせない実レベルの振動解析
~Ansys Mechanicalで実現する高度な製品開発~
-
吸入器内の粒子挙動を可視化する
~薬剤送達効率向上に向けた解析~