CAEを学ぶ
弾塑性材料モデルの基礎(第1回)
佐賀大学 大学院工学系研究科 機械システム工学専攻 只野 裕一 様
弾塑性材料モデルの基礎(第1回)の概要

弾塑性材料モデルの基礎 第1~4回 完全保存版 PDF を "無料" 公開中!

弾塑性材料モデルの基礎 完全保存版 PDF サンプル
全4回のシリーズとなっております「弾塑性材料モデルの基礎」について、4回分の解析講座を1冊でお読みいただける完全保存版 PDF を公開いたしました。どなたでも簡単なフォーム入力のみでダウンロードいただけますので、是非この機会にご利用ください。
ページ数:24 ページ
ファイル形式: PDF
佐賀大学 大学院工学系研究科
機械システム工学専攻 只野 裕一 様 著
【完全保存版 PDF 目次】
|
1. はじめに 2. 弾塑性モデルの概要 3. 弾塑性モデルを理解するための 予備知識 4. 降伏関数 |
5.ひずみ硬化則 6. 弾塑性構成式の基礎 7. おわりに |
1 はじめに
種々の機械材料に力を加えた際、材料は様々な変形応答を示します。弾性、弾塑性、超弾性、粘弾性、粘塑性など、その種類は枚挙に暇がありませんが、その中でも弾塑性は工業的に最も重要な材料の変形特性の1 つといえます。弾塑性変形は、金属や樹脂をはじめとする多くの機械材料で観察される変形特性であり、様々なものづくりの現場で現れる性質です。弾塑性は多くの複雑な変形挙動を含むため、今日に至るまで数多くのモデルが提案されてきました。現時点で、あらゆる弾塑性変形を統一的に記述できるモデルは確立していないため、ユーザーには対象となる現象に応じて適切なモデルを選択することが求められます。このため、弾塑性モデルを正しく理解することが、CAEを活用した設計においてとても重要となります。
本稿は4回に渡って弾塑性モデルの基礎を解説し、CAEの活用に必要な知識を習得して頂くことを目的としています。第1 回は、弾塑性モデルの概要と弾塑性モデルの理解に必要な予備知識を解説します。今回の内容をもとに、次回以降は降伏関数、ひずみ硬化則、弾塑性構成式の基礎について、順にご紹介していく予定です。
2 弾塑性モデルの概要
一般的な延性金属材料の単軸引張における応力・ひずみ曲線を、図1に示します。
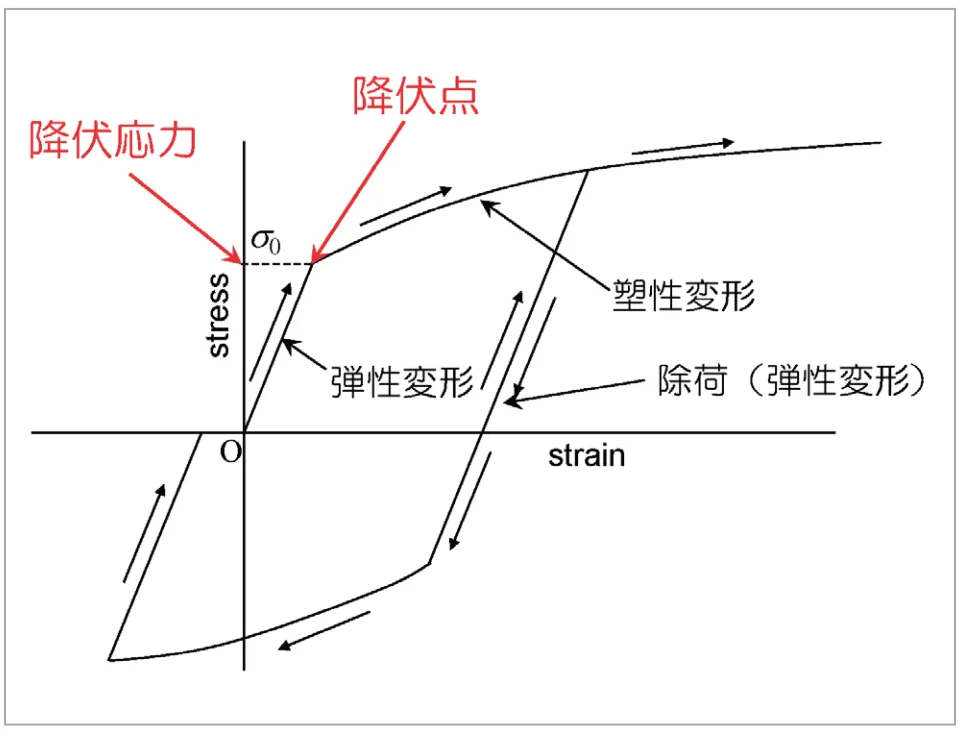
図1 弾塑性変形の概要
変形の初期において材料は弾性変形を示し、応力とひずみは比例関係となります。また荷重を取り除く、すなわち除荷すれば変形は回復し、応力がゼロとなればひずみもゼロに戻ります。しかし、応力がある値に達すると、材料は塑性変形を開始します。この材料が塑性変形を開始することを降伏、降伏を生じるときの応力を降伏応力と呼びます。材料が降伏すると、応力・ひずみ曲線の傾きは弾性変形時と比べて急激に小さくなります。これは、小さな応力増分に対して、より大きなひずみ増分を生じること意味しています。また、降伏後の応力・ひずみ曲線の傾きは一般には一定とはならず、材料によって様々な経路をたどります。さらに、塑性変形中に除荷すると、材料応答は直ちに弾性応答に戻ります。結果として、応力がゼロとなってもひずみはゼロとはならず、変形が完全には回復しません。このとき残留しているひずみを塑性ひずみと呼びます。このように、降伏後の材料の変形、すなわち塑性変形は、一般に極めて複雑で非線形性の強い現象です。この塑性変形を記述する材料モデル(構成式)には、大きく分けて3 つの因子が含まれます。
- 降伏関数(材料がいつ降伏するか)
- ひずみ硬化則(降伏後の応力がどのように変化するか)
- 塑性ひずみの発展則(塑性ひずみがどのように生じるか)
この3つを組み合わせたものが、塑性構成式であると考えることができます(狭義には、3つ目の塑性ひずみの発展則のみを指して塑性構成式と呼ぶこともあります)。塑性変形を高精度に表現するためには、 この3つの因子のそれぞれについて正しく理解し、適切なモデルを選択することが必要となります。第2回から第4回でこれらを順に解説していきますが、今回はまず塑性構成式の記述と理解に必要となるいくつかの予備知識からはじめましょう。
弾塑性モデルを理解するための 予備知識
材料の力学的挙動を数学モデルで表した構成式は、つきつめれば応力とひずみの関係を数式にしたものといえます。ですから、応力やひずみに対する正しい理解が不可欠です。ここでは、塑性材料モデルの理解に必要となる応力の取り扱いについて、いくつかの重要な事項を解説します。紙面の都合上、詳細な式導出は省略している箇所も多いので、より詳しく知りたい方は必要に応じて参考文献(例えば[1]、[2])をご参照ください。
3.1 応力テンソル
応力は、数学的にはテンソルと呼ばれる量として定義されます。テンソルとは、あるベクトルを別のベクトルへと変換する、線形変換作用素と解釈されます。テンソルの定義についての詳細は参考文献に譲りますが、ベクトルを別のベクトルへと変換するという観点からは、行列と同様の作用を持つといえます。行列とテンソルは異なる概念ですが、テンソルは結果的に行列の形式で記述できるため、ここでは応力テンソルを行列として表示した形式で取り扱うことにします。
ある応力テンソルを![]() 座標系で成分表示するとき、これを
座標系で成分表示するとき、これを
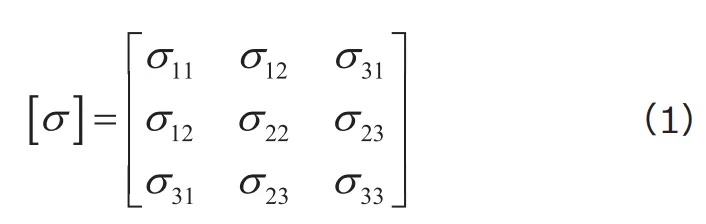
という行列![]() で表すことにしましょう。ここで、
で表すことにしましょう。ここで、![]() は各方向の垂直応力、
は各方向の垂直応力、![]() はせん断応力となります。テンソルは線形変換だと述べましたが、応力テンソルは具体的にどのような線形変換を表すのでしょうか。いま、物体のある点を通る任意の断面を考え、その単位法線ベクトルを
はせん断応力となります。テンソルは線形変換だと述べましたが、応力テンソルは具体的にどのような線形変換を表すのでしょうか。いま、物体のある点を通る任意の断面を考え、その単位法線ベクトルを![]() とします。この断面上の注目している点周りの微小面素に作用する単位面積当たりの力のベクトル(表面力ベクトル)を
とします。この断面上の注目している点周りの微小面素に作用する単位面積当たりの力のベクトル(表面力ベクトル)を![]() とすれば、応力テンソルは単位法線ベクトルを表面力ベクトルに線形変換する働きを持っています。つまり、
とすれば、応力テンソルは単位法線ベクトルを表面力ベクトルに線形変換する働きを持っています。つまり、
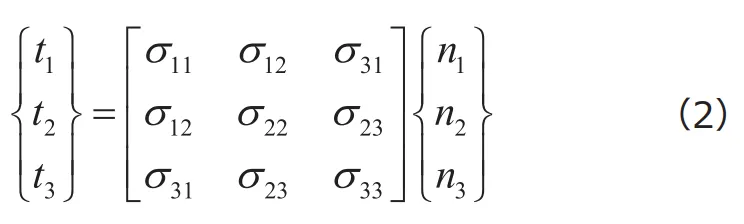
という線形変換を与えます(式(2)をコーシーの式と呼びます)。すなわち、応力テンソルは、ある点を通る任意の断面を考えたとき、その断面上の点近傍に作用する力の状態を教えてくれるテンソルなのです。
3.2 応力テンソルの座標変換
あるベクトルを異なる座標系から見ると座標系によって成分の数値が変わるように、座標系が変われば見かけの応力テンソルの成分も変化します。座標系が変われば、式(2)の単位法線ベクトルと表面力ベクトルの成分が変わるわけですから、応力テンソルの成分も変化することは容易に理解できるでしょう。ここで別の座標系として![]() 座標系を考えたとき、この座標系における応力テンソルを
座標系を考えたとき、この座標系における応力テンソルを![]() とすれば、その行列の成分は
とすれば、その行列の成分は![]() とは異なったものとなりますが、
とは異なったものとなりますが、![]() と
と![]() の間にはつぎの関係が成り立ちます。
の間にはつぎの関係が成り立ちます。
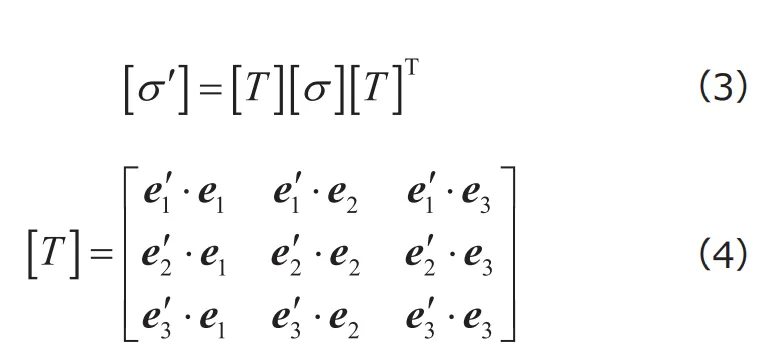
ここで、 ![]() と
と![]() はそれぞれ
はそれぞれ![]() 座標系、
座標系、![]() 座標系における基底ベクトル(座標軸と同じ方向をもつ単位ベクトル)であり、
座標系における基底ベクトル(座標軸と同じ方向をもつ単位ベクトル)であり、 ![]() ,
,![]() は2つの基底ベクトルの内積を表します。 [
は2つの基底ベクトルの内積を表します。 [![]() ]は座標変換行列と呼ばれます。座標変換の一例として、
]は座標変換行列と呼ばれます。座標変換の一例として、 ![]() 平面において平面応力とみなせる応力状態
平面において平面応力とみなせる応力状態![]() が与えられているとき、この
が与えられているとき、この![]() 面内での座標変換を考えてみましょう。
面内での座標変換を考えてみましょう。![]() 方向の応力成分は全てゼロなので、応力テンソルは2 次元的に
方向の応力成分は全てゼロなので、応力テンソルは2 次元的に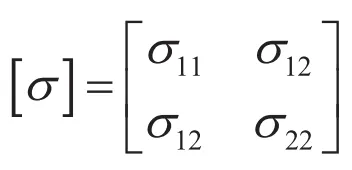 と表示できます。基準となる
と表示できます。基準となる![]() 座標系における基底ベクトルは、
座標系における基底ベクトルは、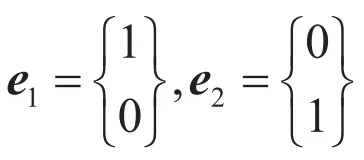 と書くことができ、またそこから反時計回りに
と書くことができ、またそこから反時計回りに![]() だけ回転した
だけ回転した![]() 座標系の基底ベクトルは
座標系の基底ベクトルは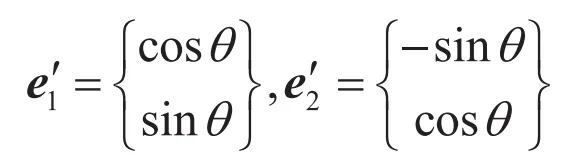 となります。これらを用いれば、座標変換行列[
となります。これらを用いれば、座標変換行列[![]() ]は
]は
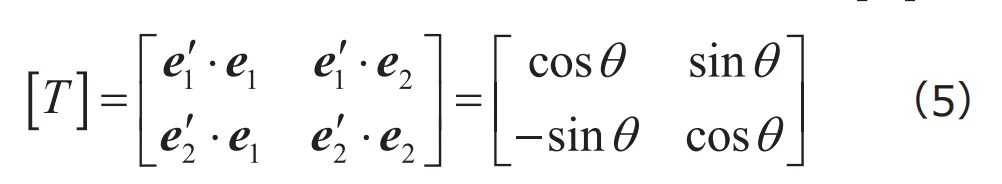
となりますから、 ![]() 座標系の応力テンソル
座標系の応力テンソル![]() は次式で求められます。
は次式で求められます。
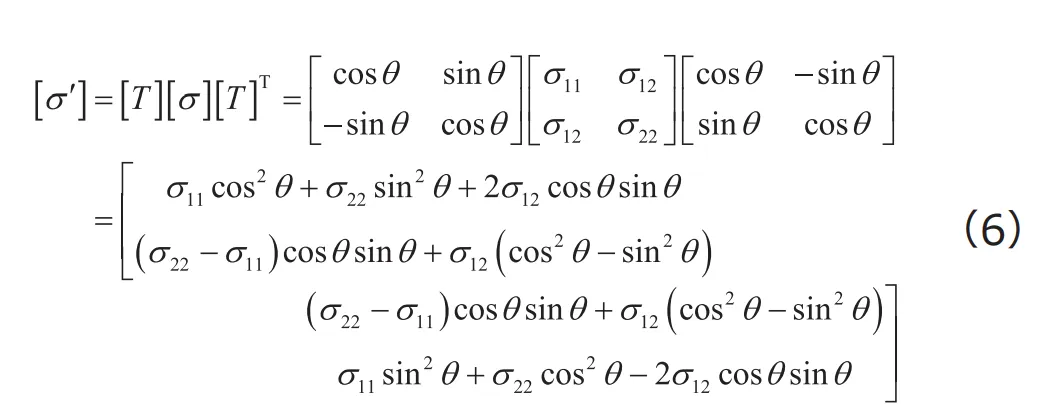
また、![]() の各成分を個別に書き出せば
の各成分を個別に書き出せば
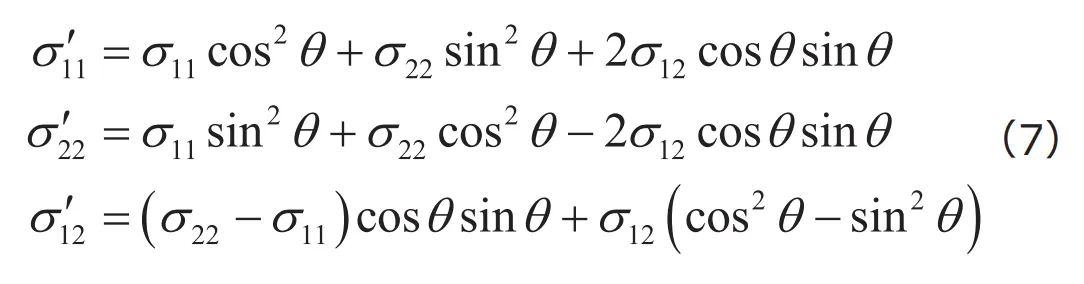
が得られます。上式は、材料力学や固体力学の教科書で紹介される2次元の応力の座標変換式に他なりません。
3.3 主応力
前節で、座標系が変わると応力テンソルの見かけの成分も変わることを示しました。座標系の取り方は任意ですから絶対的な基準は存在しませんが、誰から見ても一意に決定できるような特別な座標系が定義できれば、何かと便利に思われます。このためのひとつのアイデアが、せん断応力が全てゼロとなるような座標系を考えることです。せん断応力が全てゼロということは、応力テンソルの非対角成分が全てゼロ、すなわち応力テンソルが対角行列になるということです。これは、行列の対角化と同じ問題であり、応力テンソルの固有値を求める問題に帰着することが知られています。すなわち、つぎの固有方程式を満たす固有値![]() を求めればよいことになります。
を求めればよいことになります。
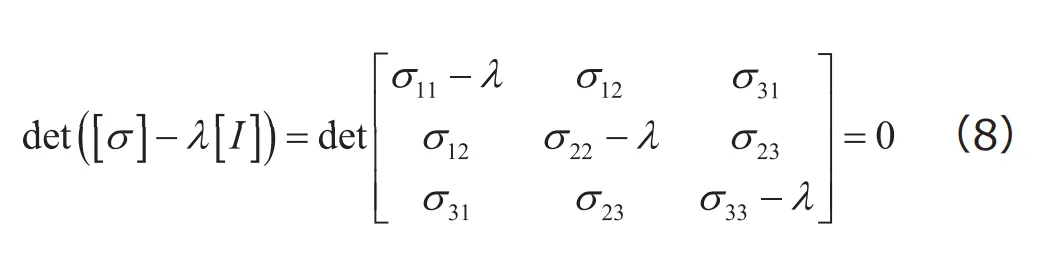
これを解いて得られる固有値![]() を主応力、それぞれの
を主応力、それぞれの![]() に対応する固有ベクトルの方向を主軸の方向と呼びます。式(8)は
に対応する固有ベクトルの方向を主軸の方向と呼びます。式(8)は![]() に対する3次方程式となることから、主応力は一般に3つ存在します。これを
に対する3次方程式となることから、主応力は一般に3つ存在します。これを![]() とすると、主軸の方向を座標軸とする
とすると、主軸の方向を座標軸とする![]() 座標系を考えたとき、この座標系での応力テンソル
座標系を考えたとき、この座標系での応力テンソル![]() は
は
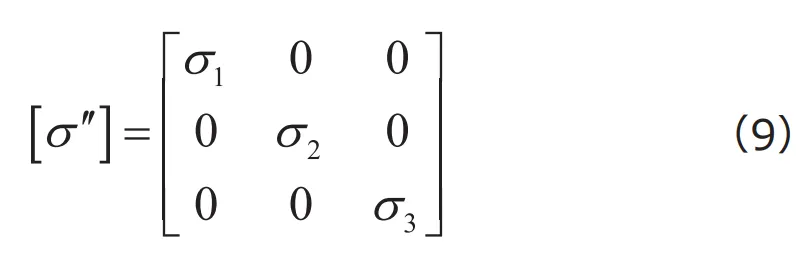
となります。なお、主応力は![]() となるように選ぶことが一般的です。注目すべきは、どのような座標系を基準として計算しても、同じ応力状態に対しては主応力は必ず同じ値となる、すなわち座標系には依存せずに一意に決定できる、ということです。
となるように選ぶことが一般的です。注目すべきは、どのような座標系を基準として計算しても、同じ応力状態に対しては主応力は必ず同じ値となる、すなわち座標系には依存せずに一意に決定できる、ということです。
座標変換や主応力をもう少しイメージしやすくするために、式(6)、(7)で得られた![]() の各成分を角度
の各成分を角度![]() の関数としてグラフにしたものが、図2です。応力の各成分が座標系によって変化し、その変化は周期的であることがわかります。
の関数としてグラフにしたものが、図2です。応力の各成分が座標系によって変化し、その変化は周期的であることがわかります。 ![]() と
と![]() はちょうど位相が90度ずれていますが、これは座標系を90 度回転させれば、2つの主軸が入れ替わることに対応しています。また、
はちょうど位相が90度ずれていますが、これは座標系を90 度回転させれば、2つの主軸が入れ替わることに対応しています。また、 ![]() もしくは
もしくは![]() が最大となるとき、もう1 つの垂直応力は最小となり、せん断応力
が最大となるとき、もう1 つの垂直応力は最小となり、せん断応力![]() はゼロとなることも確認されます。すなわち2 つの主応力が、垂直応力の取り得る最大値と最小値であることが理解できます。ちなみに、主軸の方向から45 度傾いた座標系においてはせん断応力の絶対値が最大となり、これを主せん断応力と呼びます(ただし、この座標系において、垂直応力は一般にはゼロとはなりません)。
はゼロとなることも確認されます。すなわち2 つの主応力が、垂直応力の取り得る最大値と最小値であることが理解できます。ちなみに、主軸の方向から45 度傾いた座標系においてはせん断応力の絶対値が最大となり、これを主せん断応力と呼びます(ただし、この座標系において、垂直応力は一般にはゼロとはなりません)。
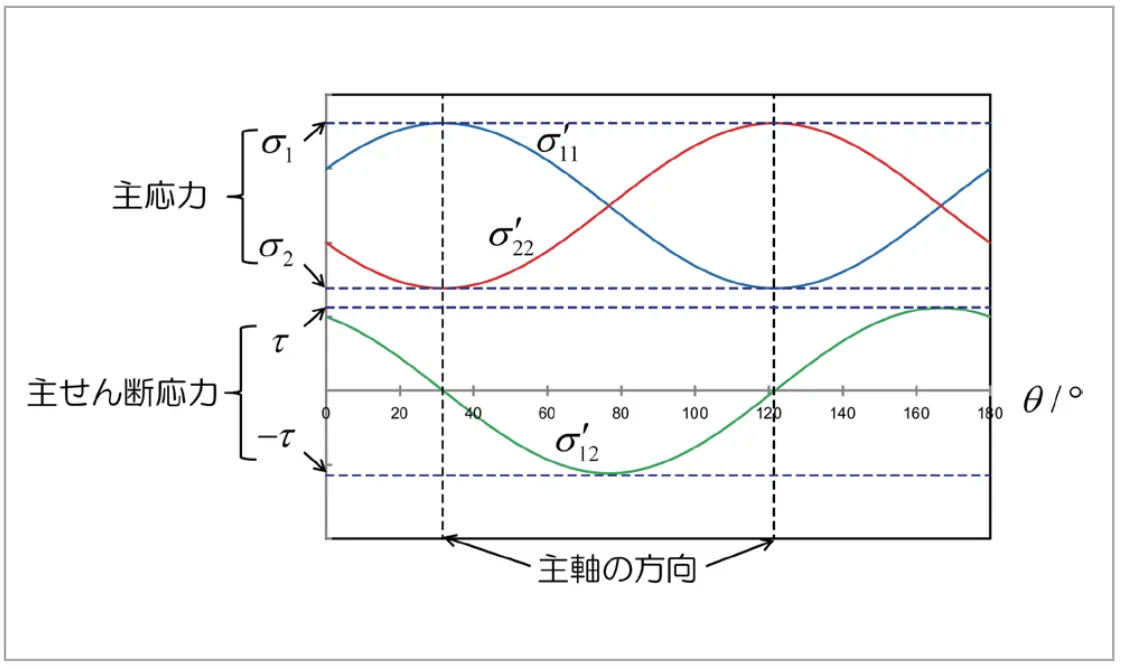
図2 平面応力状態における応力の座標変換と主応力
3.4 応力の不変量
3.2節で見たように、座標系が変われば応力テンソルの見かけの数値は変わってしまいます。ここで重要なことは、座標系の選択には任意性があり、絶対的な基準は存在しないということです。一方で、応力の座標変換は同じ物理状態を異なる座標系から見ているだけですから、座標系を変えても現象の本質が変わってはいけません。すなわち、構成式を導出する際には、座標系を変えても本質が変わらないようにする必要があります。これを満たさないと、例えばある材料を引っ張ったときに、座標系を変えるだけで観測される応力が変わってしまうという、おかしな結果を与える材料モデルが導出されてしまいます(同じ現象を見ているのに、違う座標系から見るだけで現象の本質が変わってしまう、というのは明らかに不合理です)。このような数学的要請を満たすことを、「枠無差別性」と読んでいます。厳密には「枠」という概念と座標系はイコールではないのですが、ここでは座標系に依存しないように構成式を導出しなければならない、と理解して頂いて構いません。
このように考えると、応力テンソルに対して座標系に依らず同じとなる量を定義できれば、とても都合がよいことがわかります(そのような量を使って材料モデルを定義すれば、上述の不合理は回避できるわけですから)。例えばベクトルの場合、どのような座標系でベクトルを成分表示しても、その長さ(ノルム)は変わりません。このような量を不変量と呼びます。前節で求めた主応力は、応力テンソルの不変量としての資格を持っています。
応力テンソルに対する不変量には様々な定義が可能ですが、ここでは材料モデリングにおいて特に重要な3つの不変量を紹介します。主応力を求めるための固有方程式(式(8))を思い出しましょう。固有方程式は固有値![]() に対する3 次方程式なので、つぎの一般形で表すことができます。
に対する3 次方程式なので、つぎの一般形で表すことができます。
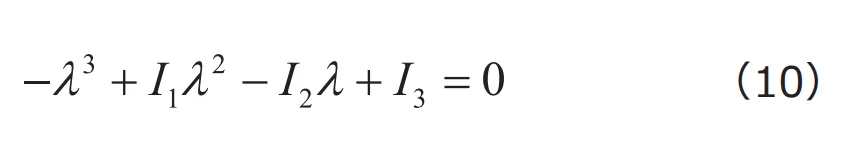
固有方程式は、どの座標系の応力成分から立式しても同じ固有値を与えることから、係数![]() は座標系によらず同じ値になるはずです。これを具体的に計算すると、つぎのようになります。
は座標系によらず同じ値になるはずです。これを具体的に計算すると、つぎのようになります。
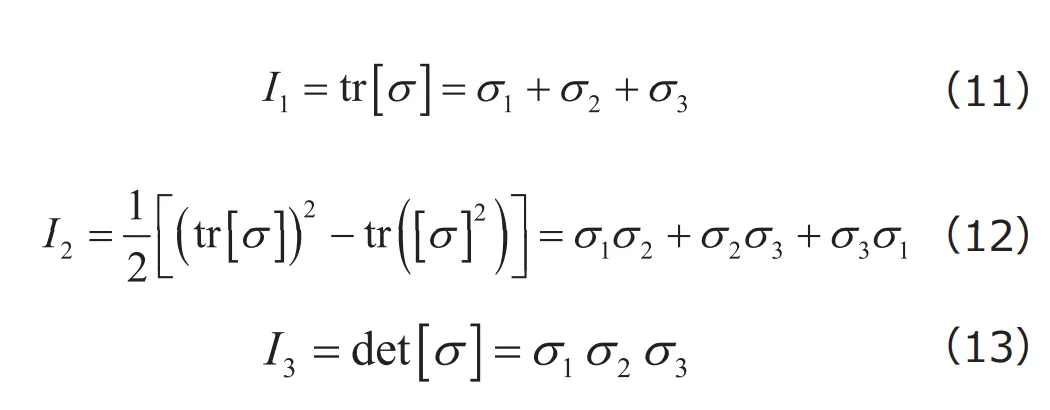
ここで![]() 、
、![]() はそれぞれ
はそれぞれ![]() のトレースと行列式です。
のトレースと行列式です。![]() は座標系によらないことからは座標系によらないことから、応力テンソルの不変量となります。これらの不変量をそれぞれ応力テンソルの第1 、第2 、第3不変量、3つをまとめて主不変量と呼んでおり、弾塑性材料に限らず、材料モデルを構築する際に重要な役割を果たす量となります。
は座標系によらないことからは座標系によらないことから、応力テンソルの不変量となります。これらの不変量をそれぞれ応力テンソルの第1 、第2 、第3不変量、3つをまとめて主不変量と呼んでおり、弾塑性材料に限らず、材料モデルを構築する際に重要な役割を果たす量となります。
不変量の直感的な理解を助けるために、その幾何学的解釈を少し紹介しましょう。線形変換は一般に、幾何学的には図形の変換を意味しています。例えば2次元空間において原点を中心とする単位円を考えると、実行列による線形変換はこれを楕円に変換します。平面応力状態における応力テンソルも同様の性質を持っており、線形変換後の楕円の長径と短径が2 つの主応力の大きさに対応します。また応力の座標変換は、この楕円を回転させる操作に対応します。このように考えると、座標変換しても主応力が変わらないことが理解できるのではないでしょうか(回転させるだけなので、楕円の長径と短径は不変です)。これを図3に模式的に図示します。
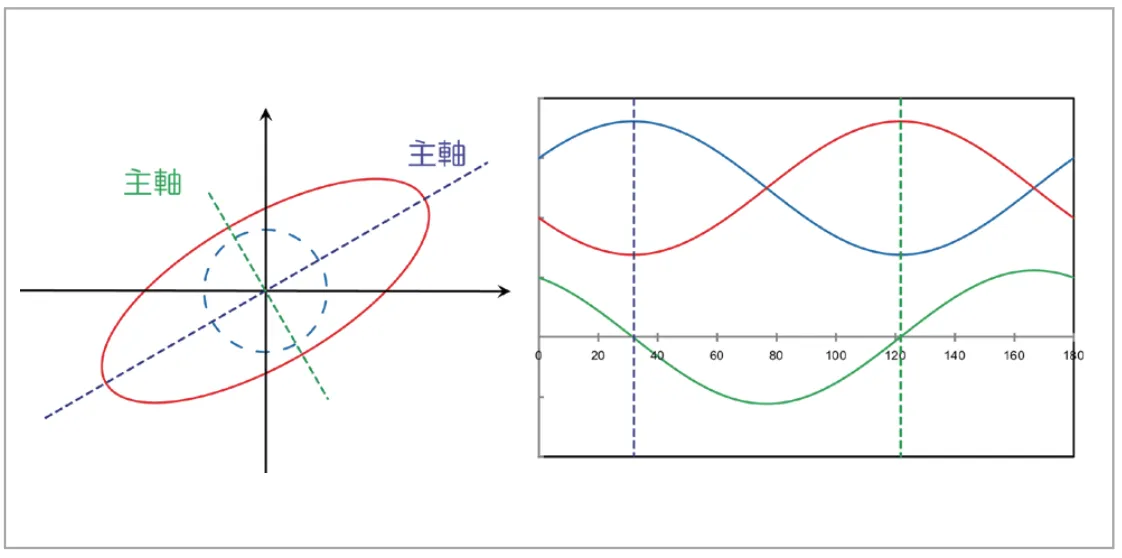
図3 応力の座標変換とその幾何学的イメージ
このイメージをもとに、例えば第1 不変量を考えてみると、第1不変量は長径と短径の和となりますから座標変換に対して不変です。同様に第2 不変量は、楕円に外接する長方形の面積の![]() になり、これも座標変換に対してその大きさを変えることはありません。第3不変量については、平面応力状態では常にゼロとなってしまうのですが、3次元的な応力状態においては楕円を楕円球に置き換えて解釈することができ、第3不変量はこの楕円球に外接する直方体の体積の
になり、これも座標変換に対してその大きさを変えることはありません。第3不変量については、平面応力状態では常にゼロとなってしまうのですが、3次元的な応力状態においては楕円を楕円球に置き換えて解釈することができ、第3不変量はこの楕円球に外接する直方体の体積の![]() となりますが、やはり座標変換によってその大きさは変わりません。このように、いずれの主不変量も、幾何学的には座標変換しても変わらない量(長さ、面積、体積)に対応していることがわかります。この解釈の詳細は、文献[1]を参照ください。
となりますが、やはり座標変換によってその大きさは変わりません。このように、いずれの主不変量も、幾何学的には座標変換しても変わらない量(長さ、面積、体積)に対応していることがわかります。この解釈の詳細は、文献[1]を参照ください。
3.5 平均応力と偏差応力
応力テンソルの第1不変量を![]() 倍した量を、平均応力もしくは静水圧と呼びます。これを
倍した量を、平均応力もしくは静水圧と呼びます。これを![]() と表記することにすれば、
と表記することにすれば、
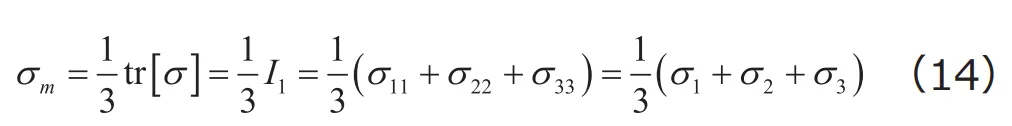
となります。第1不変量を![]() 倍しただけですから、
倍しただけですから、![]() も不変量となり座標系には依存しません。この
も不変量となり座標系には依存しません。この![]() を対角成分に持つ応力テンソルを、平均応力テンソルと呼びます。これを[
を対角成分に持つ応力テンソルを、平均応力テンソルと呼びます。これを[![]() ]とすれば
]とすれば
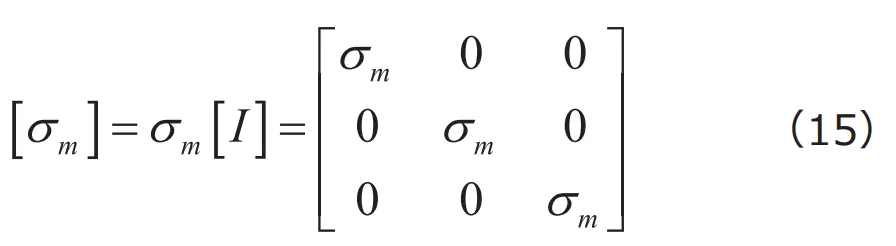
と表現されます。平均応力テンソル[![]() ]も一種の応力テンソルとみなせることから、その座標変換を考えてみます。
]も一種の応力テンソルとみなせることから、その座標変換を考えてみます。
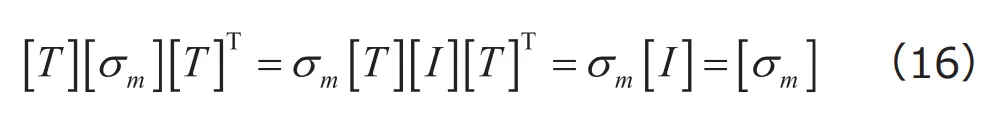
上式は、平均応力テンソルは座標変換しても不変、すなわち任意の座標系で平均応力テンソルは同じ成分を有することを意味しています。ちなみに平均応力テンソルの固有方程式を考えると、固有値(主応力)は三重根となり![]() 、さらに特定の主軸を持たないことが導かれます。これは、平均応力テンソルは、全ての方向から均一な応力が加えられている状態を表していることを意味しています。すなわち、平均応力テンソルは全方向から一様な垂直応力が働いている状態を表し、平均応力
、さらに特定の主軸を持たないことが導かれます。これは、平均応力テンソルは、全ての方向から均一な応力が加えられている状態を表していることを意味しています。すなわち、平均応力テンソルは全方向から一様な垂直応力が働いている状態を表し、平均応力![]() はその大きさであるといえます。見方を変えれば、平均応力
はその大きさであるといえます。見方を変えれば、平均応力![]() は流れのない流体による圧力(これはあらゆる方向からまんべんなく加わります)と同様の応力状態に対応しており、これが静水圧とも呼ばれる所以です。
は流れのない流体による圧力(これはあらゆる方向からまんべんなく加わります)と同様の応力状態に対応しており、これが静水圧とも呼ばれる所以です。
つぎに、応力テンソルから平均応力テンソルを引いて得られる量を定義しましょう。
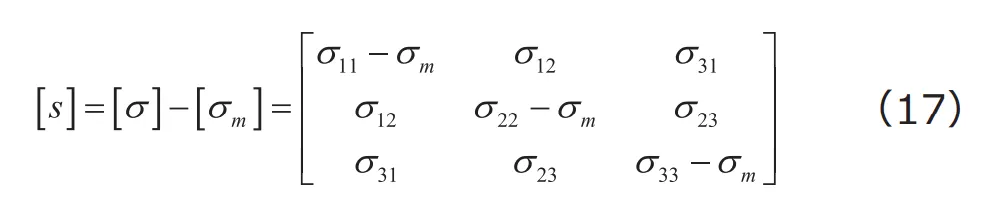
この[![]() ]を偏差応力テンソルと呼びます。偏差応力テンソルにおいて、成分が変化するのは垂直応力だけであり、せん断応力は変わりません。応力テンソルから平均応力テンソルを除いた量である偏差応力テンソルは、せん断応力を特徴づけるテンソルであると解釈できます。この偏差応力テンソルは、次回解説する降伏関数や、第4回で取り扱う弾塑性構成式の記述において、重要な量となります。なお偏差応力テンソルは、座標系によって見かけの数値が変化することに注意しましょう。
]を偏差応力テンソルと呼びます。偏差応力テンソルにおいて、成分が変化するのは垂直応力だけであり、せん断応力は変わりません。応力テンソルから平均応力テンソルを除いた量である偏差応力テンソルは、せん断応力を特徴づけるテンソルであると解釈できます。この偏差応力テンソルは、次回解説する降伏関数や、第4回で取り扱う弾塑性構成式の記述において、重要な量となります。なお偏差応力テンソルは、座標系によって見かけの数値が変化することに注意しましょう。
以上より、応力テンソル![]() は平均応力テンソル[
は平均応力テンソル[![]() ]と偏差応力テンソル[
]と偏差応力テンソル[![]() ]の和で表せることになります。
]の和で表せることになります。
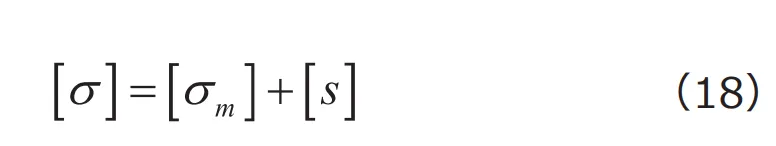
これは、ある応力状態を全ての方向から等しく加わる応力成分と、せん断応力的な成分に分解できることを意味しています。1つ注意が必要なのが、平均応力テンソルや偏差応力テンソルは、例え応力が1次元的もしくは2次元的な状態であっても、常に3次元的な成分を有するということです。このことは、弾塑性構成式の理解において重要な意味を持ちますので、記憶に留めておいてください。
第1 回となる今回は、弾塑性モデルの概要と弾塑性モデルの理解に必要な予備知識を解説しました。具体的な弾塑性モデルに関する記述までたどり着いていないため、物足りないと感じられたかも知れませんが、ここで学んだ数学的知識は次回以降の理解に重要となります。今回の内容を踏まえて、次回は材料の降伏を記述するための、降伏関数について解説します。
参考文献
[1] 石井、只野、加藤、車谷、例題で学ぶ連続体力学、森北出版、2014
[2] 有光、はじめての固体力学、講談社、2010
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

コントローラ&センサのデータ駆動型シミュレーション
~データ駆動によるロボットのモデリングと制御設計~
-

EMCのお悩みありませんか? ~EMCソリューション~
-

炭素回収・利用・貯留におけるCO2の削減 ~Ansys Fluentによるソリューション~
~Ansys Fluentによるソリューション~
-

仮想環境で実現するマシンビジョン設計~Ansys Speosによるカメラ&照明最適化ソリューション~
~Ansys Speosによるカメラ&照明最適化ソリューション~
-
構想設計ですぐにリアルタイム検証 ~解析専任者ゼロでも使いこなせるAnsys Discovery~
~解析専任者ゼロでも使いこなせるAnsys Discovery~
-
流体機器設計の新たな一歩
~Ansys Discoveryで加速する設計改革~
-
筐体の冷却性能を構想設計から見える化 (手戻りを削減できる)
~Ansys Discoveryで始める電気筐体製品の設計改革~
-
若手でもすぐに使えるリアルタイム解析 (勘と経験からの脱却)
~Ansys Discoveryによる30名規模メーカーの設計改革~