製品
Homogenization analysis of composite resin with oriented fiber
Introducing the example of creep homogenization analysis on the composite material that consists of a resin which has the creep characteristics and fiber that is an elastic body and oriented at ±30°. In addition, identifying the material properties value of the anisotropic creep using optimization based on the material test data of these.
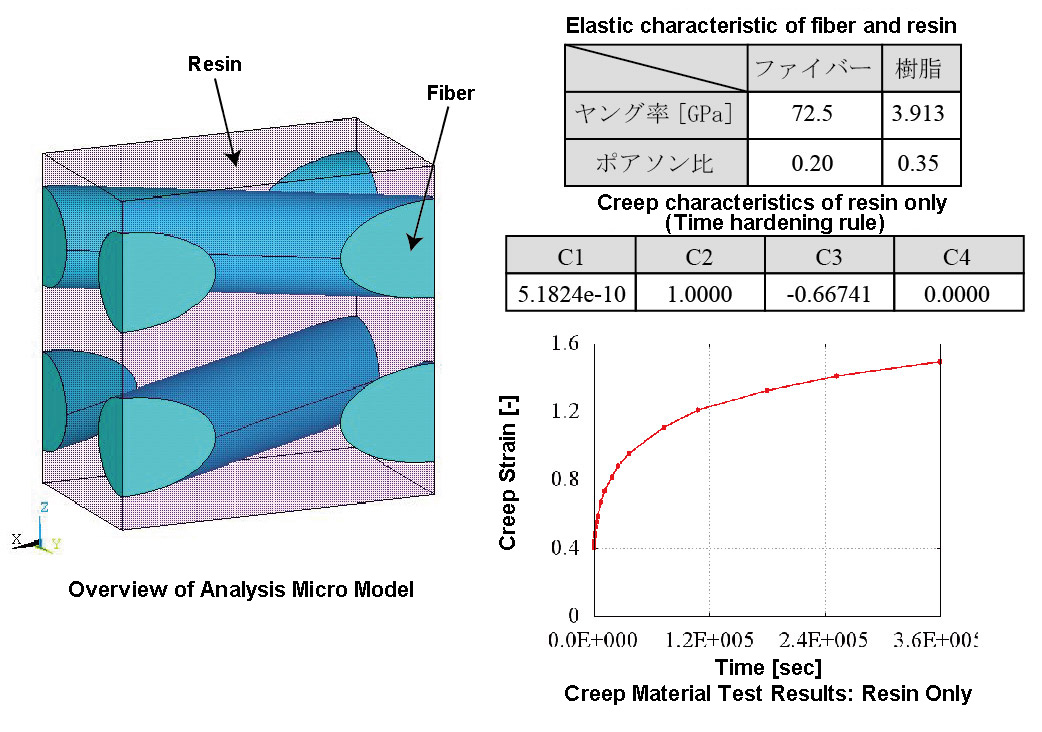
Analysis Model
- Numerical material test with constant load performed on micro-model shown in Figure 1 and obtaining creep material characteristics in three uniaxial directions and three pure shear directions respectively.
- Performing identification of anisotropic creep material property value using optimization based on this material test data.
Analysis Results
Material Test Results
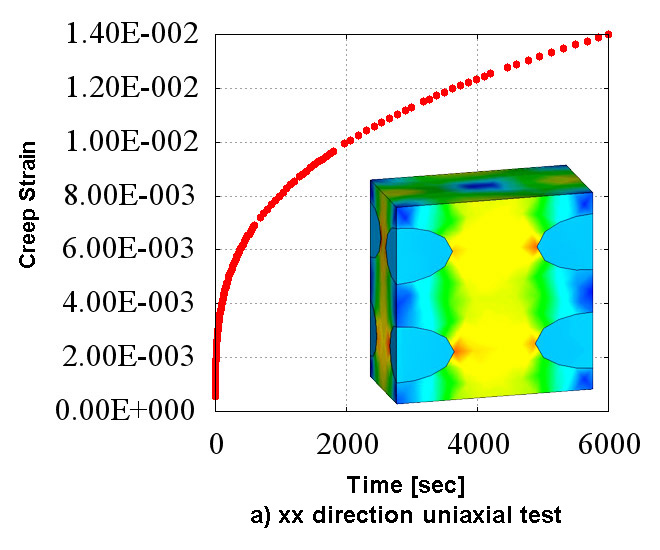
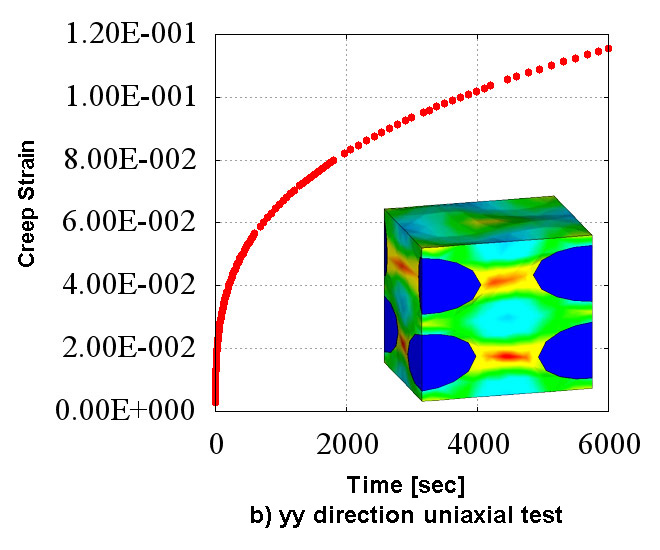
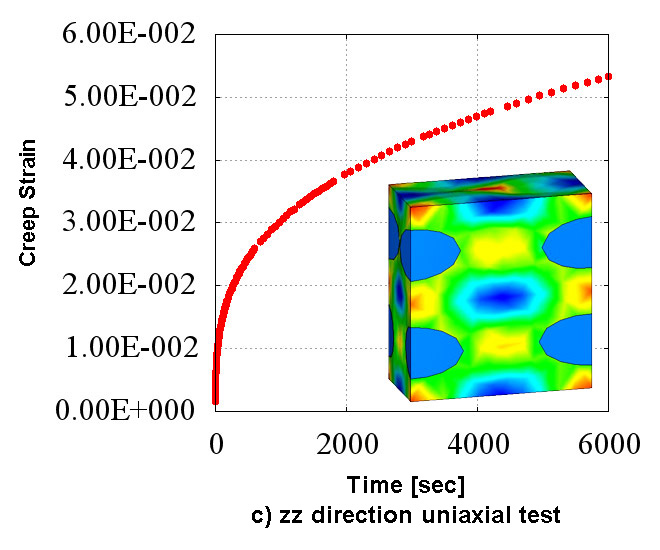
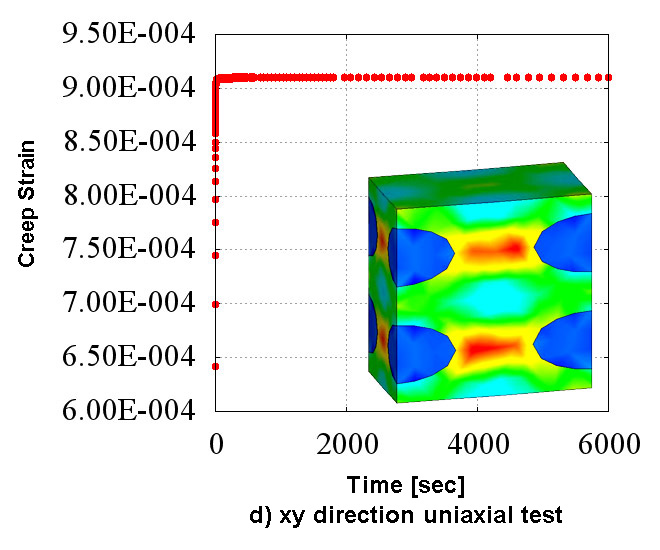
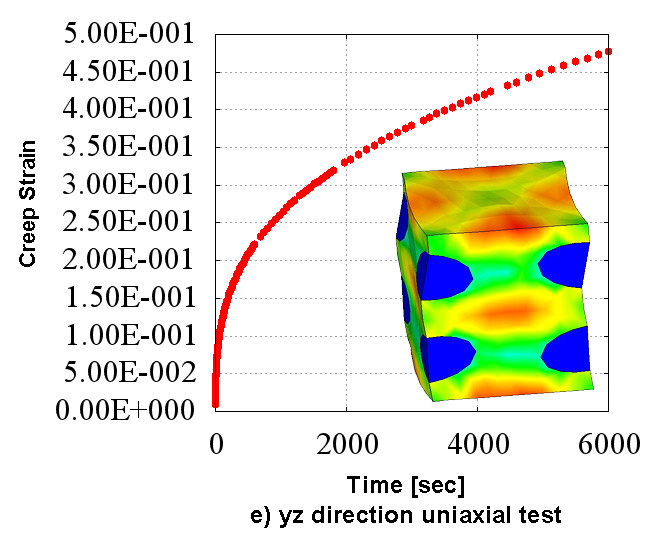
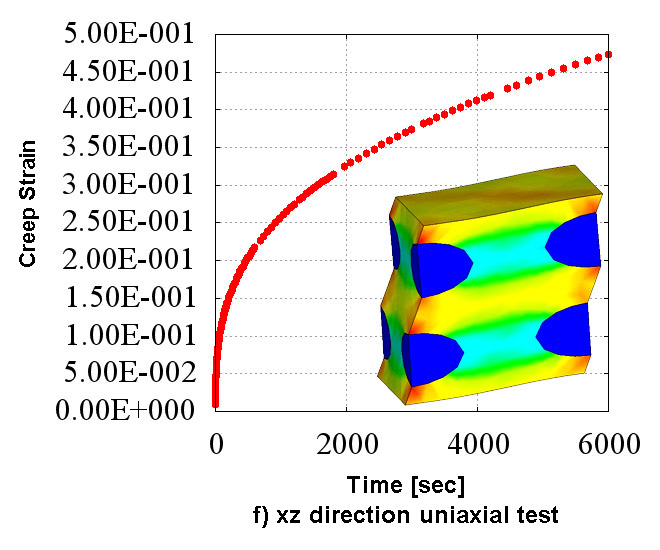
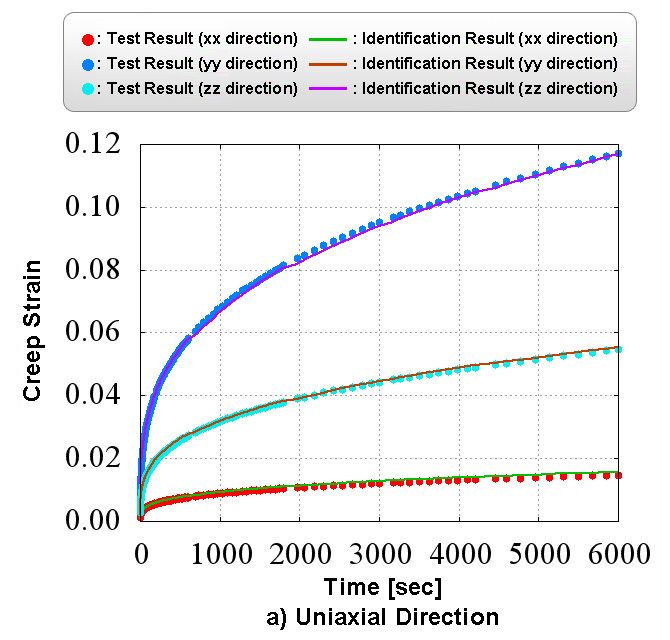
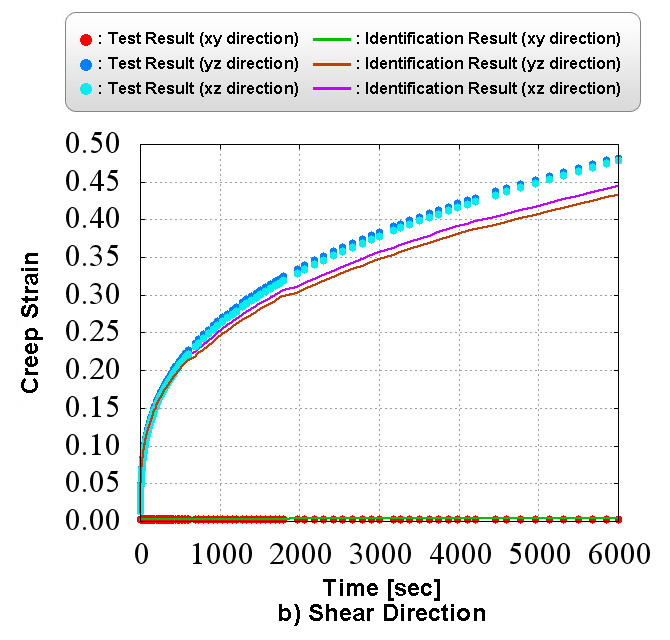
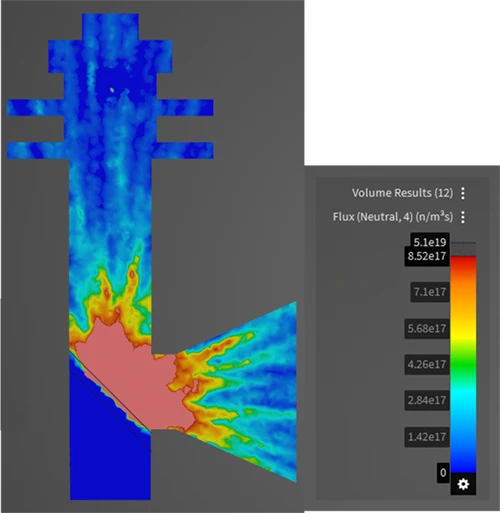
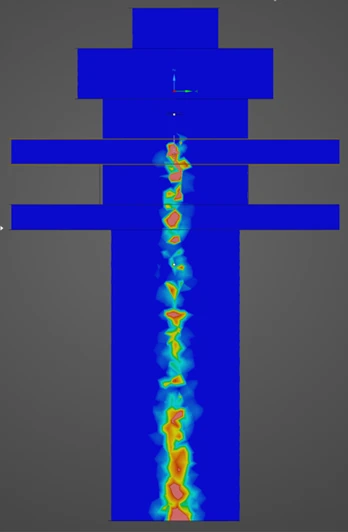
Figure 2 shows the creep material characteristics of six directions obtained in the numerical material test. You can see the state which has the "anisotropy" that characteristics are different in all directions. Also, looking at Figure 2 which shows the analysis results of d) xy direction pure shear test, it does not show the creep characteristics compared to the other directions since the fibers oriented in the in-plane direction are mainly responsible for the load. In CMAS, these complex behaviors of heterogeneous materials can be observed conveniently in a virtual environment without relying on actual costly tests.
Identification results
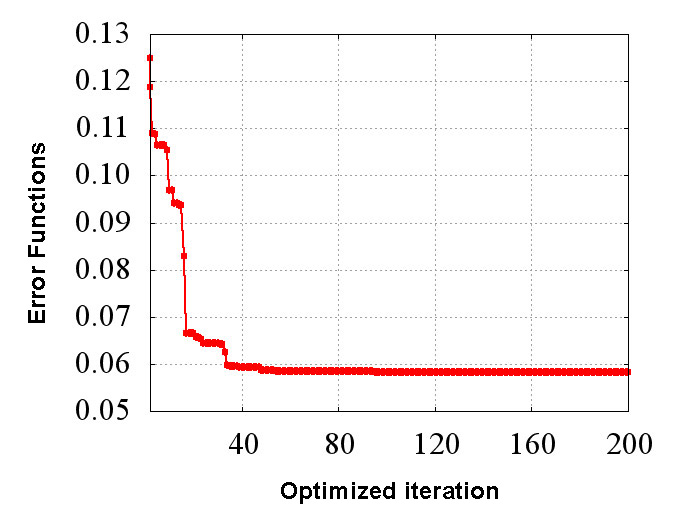
These are the identification results of anisotropic creep material properties based on the behavior of the numerical material testing which is calculated above. Figure 3 is a graph showing the convergence history of the error function that is minimized in the optimization algorithm. In this case, we define the difference between the response of the material constitutive law and material test results as the error function. You can achieve good convergence tendency without having special skills in CMAS since it has adopted Particle Swarm Optimization (PSO) and it is not necessary to specify the fitting parameters.
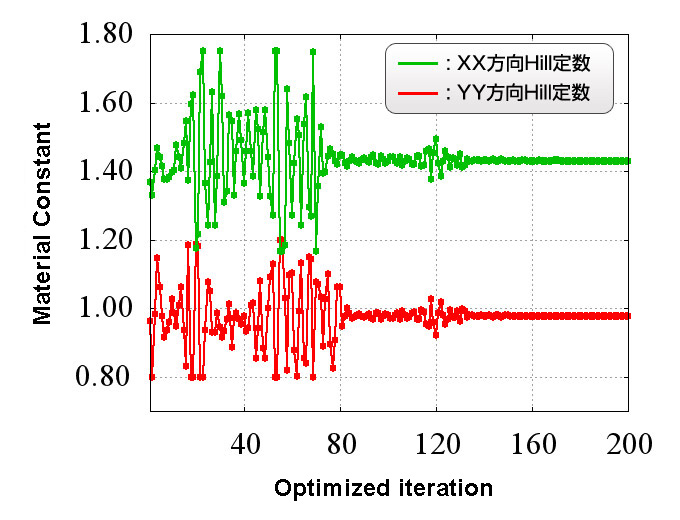
Figure 4 shows the convergence history of the material property value (Hill constant).
You can see that along with the increase in the optimized iterations, values converge on a certain constant material
property value.
Figure 5 shows a comparison of material test data and identification results.
You can verify the validity of the fitting results by comparing the two.
Analysis Types
Structural Analysis、 Mutiscale Analysis、 Homogenization Analysis
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

【全記事】CAEのあるものづくり vol.42
ユーザー様インタビュー記事7件を1冊に集約した保存版
-

誤差との上手なつきあい方 ~流体解析の計算誤差~ (完全保存版)
誤差との上手なつきあい方 前編・後編 を1冊にまとめた保存版 PDF
-

非線形解析の最大強度評価はAnsys LS-DYNAで解決!
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析で電子機器の信頼性向上
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

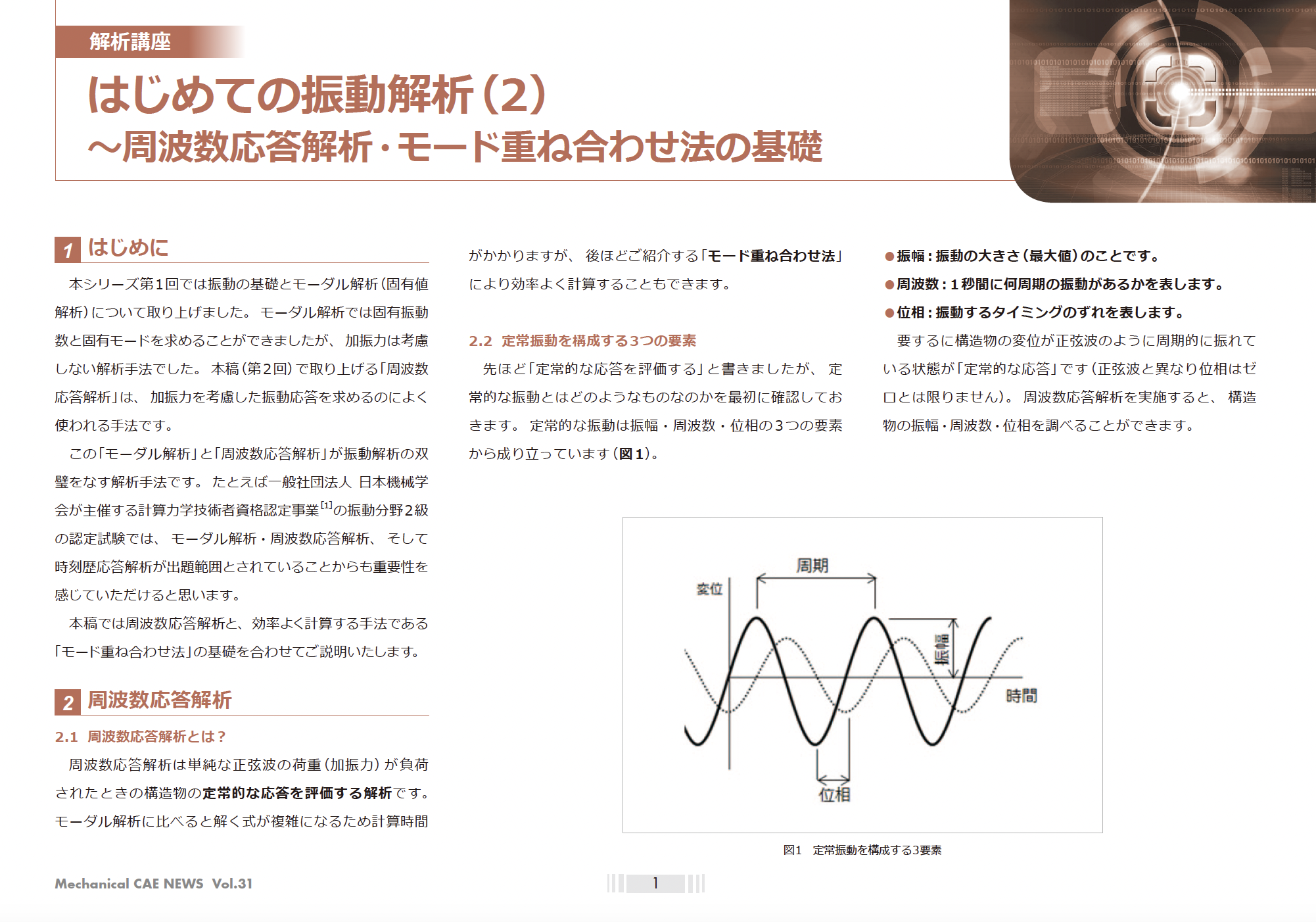
共振回避だけで終わらせない振動解析の進め方を解説(周波数応答・時刻歴まで)
~Ansys Mechanicalで実現する高度な製品開発~
-
吸入器内の粒子挙動を可視化することで薬剤送達効率の向上へ
~薬剤送達効率向上に向けた解析~