クーラン条件(くーらんじょうけん)

クーラン条件とは、陽解法動解析において、解の安定限界を保証するためには、時間増分Δtがクリティカル時間ステップサイズ（Δt ^crit ）よりも小さくなければならないことを表したものです。
CFL条件（Courant-Friedrichs-Lewy Condition）とも呼ばれます。

クリティカル時間ステップサイズ（Δt ^crit ）がどのぐらいになるのか、ロッドを例に検討してみます。

ロッドの固有振動数は次のようになります。

従って、ロッドのクリティカル時間ステップサイズ（Δt ^crit ）は以下のように求められます。

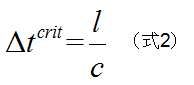
このΔt ^crit は、長さ l のロッド内を弾性波が伝わるのに必要な時間です。

解析モデル全体で Δt ^crit が最も小さくなるのは、ｌが最も小さい、すなわち要素長さが最も小さい箇所となります。
従って、解析モデル全体でのΔt ^crit は以下のように求められます。

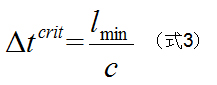
陽解法時間積分におけるクリティカル時間ステップサイズは、最小要素長さl _min と材料特性（音速c）に依存することがわかります。

安定的に解析するには、解析中、時間増分ΔtはΔt ^crit よりも小さくする必要があり、このことをクーラン条件（Courant-Friedrichs-Levy-criterion）と呼びます。

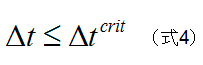
通常、時間ステップサイズは非常に小さく、時刻歴応答を得るためには多くの時間ステップでの計算が必要になります。

例：メッシュサイズが1mmで音速が5000m/sの場合、時間ステップは0.18μsecとなり、0.1秒の時刻歴応答を得るためには、555,556ステップの計算が必要となります。

Ansysにおける取扱い

• Ansysの陽解法動解析では、クーラン条件を満足するように自動的に時間ステップを調整します。

CAE用語辞典の転載・複製・引用・リンクなどについては、「著作権についてのお願い」をご確認ください。