CAEを学ぶ
弾塑性材料モデルの基礎(第4回)
佐賀大学 大学院工学系研究科 機械システム工学専攻 只野 裕一 様
弾塑性材料モデルの基礎(第4回)の概要

弾塑性材料モデルの基礎 第1~4回 完全保存版 PDF を "無料" 公開中!

弾塑性材料モデルの基礎 完全保存版 PDF サンプル
これさえ読めば”弾塑性材料モデルの基礎”がわかる
全4回のシリーズとなっております「弾塑性材料モデルの基礎」について、4回分の解析講座を1冊でお読みいただける完全保存版 PDF を公開いたしました。どなたでも簡単なフォーム入力のみでダウンロードいただけますので、是非この機会にご利用ください。
ページ数:24 ページ
ファイル形式: PDF
佐賀大学 大学院工学系研究科
機械システム工学専攻 只野 裕一 様 著
【完全保存版 PDF 目次】
|
1. はじめに 2. 弾塑性モデルの概要 3. 弾塑性モデルを理解するための 予備知識 4. 降伏関数 |
5.ひずみ硬化則 6. 弾塑性構成式の基礎 7. おわりに |
5 ひずみ硬化則(承前)
5.4 ひずみ硬化に伴う降伏曲面の変化
第2回、第3回で述べたように、弾塑性構成式では塑性変形進行中、応力は常に降伏曲面上にあると仮定してモデル化されます。これは、塑性変形に伴うひずみ硬化やひずみ軟化によって、降伏曲面が変化することを意味しています。前回解説した相当応力と相当塑性ひずみの関係を表すひずみ硬化則により、スカラー量としての降伏応力の発展は表現することができますが、3次元的な応力状態においては、降伏曲面の変化を記述するためのモデルも別途必要となります。このモデルは、繰り返し負荷問題(除荷と再降伏を繰り返す問題)や、板材の曲げ加工などにおけるスプリングバック(除荷によって弾性変形が回復することで、最終的な変形が最大変形よりも少し小さくなる現象)の予測において特に重要となります。このため、実用的な弾塑性解析においては、適切なモデルの選択やパラメータ同定が重要です。
ここでは、降伏曲面の変化を記述するための、基本的ないくつかのモデルについて解説します。第2 回で述べたように、主応力を用いることで降伏曲面を3 次元空間に記述することができます。ここではさらに、主応力空間で![]() となる平面上の降伏曲面を考えることにしましょう。このような平面を
となる平面上の降伏曲面を考えることにしましょう。このような平面を![]() 平面と呼びます。例えば、Misesの降伏曲面は
平面と呼びます。例えば、Misesの降伏曲面は![]() 平面では真円、Trescaの降伏曲面はこれに内接する正六角形となります。
平面では真円、Trescaの降伏曲面はこれに内接する正六角形となります。![]() 平面を用いることで、降伏曲面の変化の様子をイメージしやすくなります。
平面を用いることで、降伏曲面の変化の様子をイメージしやすくなります。
5.4.1 弾完全塑性モデル
まず最も単純なケースとして、全くひずみ硬化が生じないモデルを考えてみましょう。応力が初期降伏曲面上に達すると初期降伏が発生しますが、ひずみ硬化が生じないということは、応力が初期降伏曲面より外の状態をとることがない、すなわち塑性変形中に降伏曲面が全く変化しないモデルとなります。 これを弾完全塑性モデルと呼びます。
図1に、弾完全塑性モデルを模式的に示します。左図は![]() 平面における降伏曲面、右図は単軸引張・圧縮時の応力・ひずみ線図となります。
平面における降伏曲面、右図は単軸引張・圧縮時の応力・ひずみ線図となります。![]() 平面上で見ると、初期降伏後に応力が降伏曲面上を移動することは可能ですが、降伏曲面の外側の応力状態にはなりません。これを単軸引張・圧縮で考えた場合、初期降伏後は一定の降伏応力のまま塑性ひずみが増大し、ひずみ硬化が全く生じないことに対応します。また、引張後に負荷方向を反転して圧縮に転じる場合(もしくはその逆の場合)、引張(もしくは圧縮)で降伏した際と絶対値が同じ応力で再降伏することになります。弾完全塑性モデルでは、ひずみ硬化挙動は全く表現されませんが、ひずみ硬化の影響が相対的に小さく、初期降伏後の応力上昇が無視できる程度の場合であれば、近似的なモデルとして有効となります。
平面上で見ると、初期降伏後に応力が降伏曲面上を移動することは可能ですが、降伏曲面の外側の応力状態にはなりません。これを単軸引張・圧縮で考えた場合、初期降伏後は一定の降伏応力のまま塑性ひずみが増大し、ひずみ硬化が全く生じないことに対応します。また、引張後に負荷方向を反転して圧縮に転じる場合(もしくはその逆の場合)、引張(もしくは圧縮)で降伏した際と絶対値が同じ応力で再降伏することになります。弾完全塑性モデルでは、ひずみ硬化挙動は全く表現されませんが、ひずみ硬化の影響が相対的に小さく、初期降伏後の応力上昇が無視できる程度の場合であれば、近似的なモデルとして有効となります。
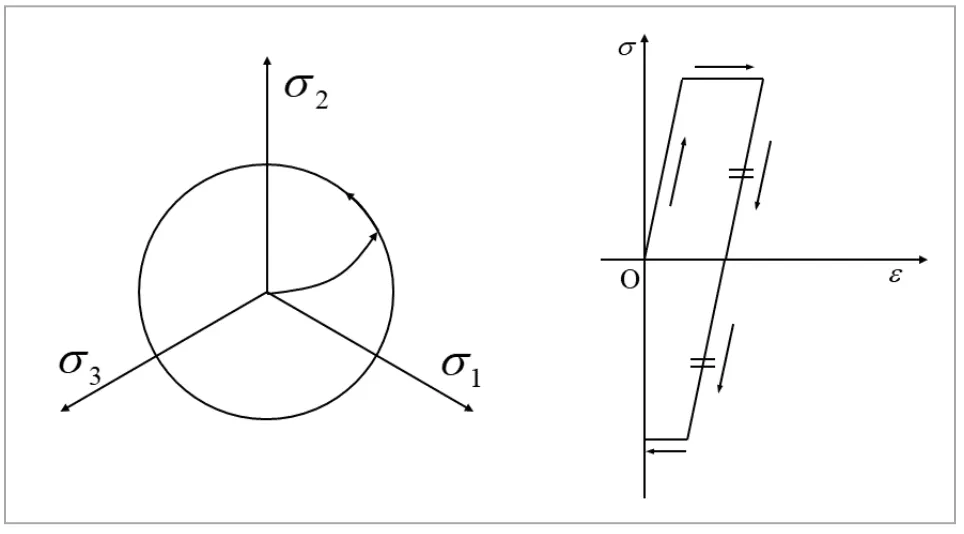
図1 弾完全塑性モデル(ひずみ硬化なし)
5.4.2 等方硬化則
つぎに、ひずみ硬化を生じる場合について考えてみましょう。ひずみ硬化を生じるということは、初期降伏後に降伏曲面が変化し、応力が常に降伏曲面上に存在するようにする必要があります。このための考え方の一つが、降伏曲面が相似形を保ったまま大きさを変える(降伏曲面が相似的に膨張する)とする方法です。例えばMisesの降伏関数を考えるとき、![]() 平面上では降伏曲面は原点を中心としたまま半径が変化することに対応します。また、弾性除荷時には、応力が降伏曲面の内側へと移動しますが、このとき降伏曲面は変化しない(膨張したまま)と考えます。
平面上では降伏曲面は原点を中心としたまま半径が変化することに対応します。また、弾性除荷時には、応力が降伏曲面の内側へと移動しますが、このとき降伏曲面は変化しない(膨張したまま)と考えます。
このようなモデルを、等方硬化則と呼びます。等方硬化則の概略を図2に示します。左図において破線で示される初期降伏曲面に応力が達すると材料は降伏しますが、そこから応力が外側の状態をとろうとすると、降伏曲面が応力に引きずられるように膨張します。
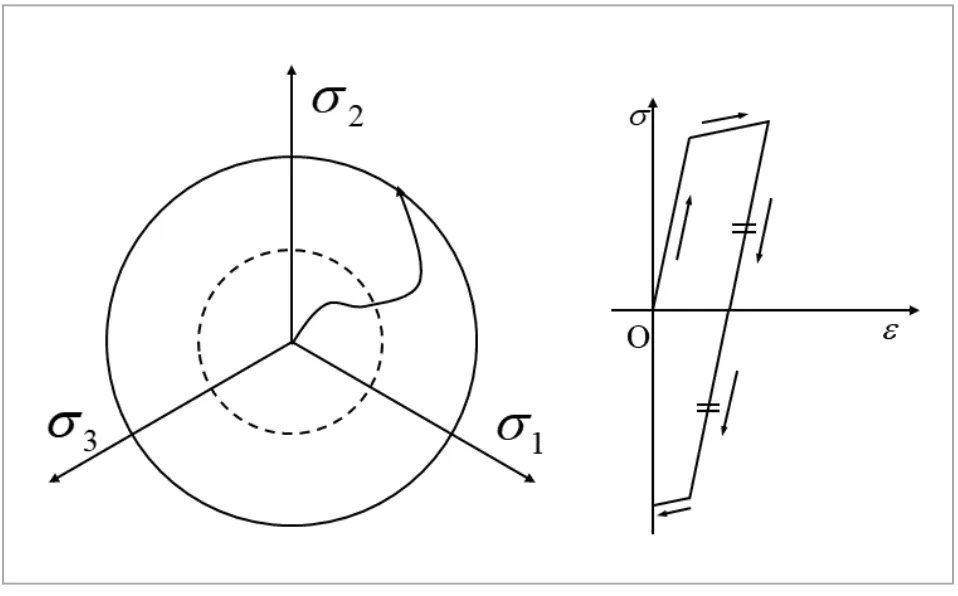
図2 等方硬化則
例として、単軸引張・圧縮状態を考えてみましょう。材料の初期降伏応力が![]() であるとすると、初期降伏曲面は原点を中心とする円であり、この半径が
であるとすると、初期降伏曲面は原点を中心とする円であり、この半径が![]() に対応するとイメージできます(正確には、
に対応するとイメージできます(正確には、![]() 平面上でのMisesの降伏曲面は半径
平面上でのMisesの降伏曲面は半径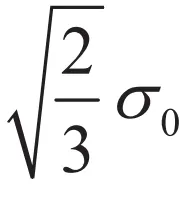 の円となります)。この材料を単軸引張まで
の円となります)。この材料を単軸引張まで![]() 引っ張ったとき、降伏曲面は原点を中心としたまま、半径
引っ張ったとき、降伏曲面は原点を中心としたまま、半径![]() が倍の円へと膨張します。この状態から除荷を行うと、降伏曲面の大きさはそのままに、材料は弾性状態に戻ります。ですから、再負荷すると
が倍の円へと膨張します。この状態から除荷を行うと、降伏曲面の大きさはそのままに、材料は弾性状態に戻ります。ですから、再負荷すると![]() では再降伏せず、応力が
では再降伏せず、応力が![]() に達して初めて再降伏します。もしくは、除荷後に圧縮へと負荷方向を反転させると、
に達して初めて再降伏します。もしくは、除荷後に圧縮へと負荷方向を反転させると、![]() で材料は降伏することになります。
で材料は降伏することになります。
このように、等方硬化則を用いることで、除荷時の再降伏において降伏応力が除荷直前の応力となることを表現できますが、引張後に圧縮(もしくはその逆)をした際に降伏応力が低下するという、 Bauschinger効果を表現できません。そこで、つぎの移動硬化則が提案されました。
5.4.3 移動硬化則
移動硬化則では、応力が降伏曲面の外側の状態をとろうとするとき、降伏曲面が大きさや形はそのままに位置を変えると考え、応力が常に降伏曲面上に存在することをモデル化します。Misesの降伏関数を考えるのであれば、平面上において降伏曲面は常に初期状態の半径を持った円のままであり、塑性変形の進行とともに降伏曲面が移動することになります。移動硬化則の概略を図3に示します。応力が初期降伏曲面の外側へと遷移しようとすると、降伏曲面が応力に引きずられるように移動することになりますが、これは降伏曲面の中心が移動していると解釈することができます。応力空間における降伏曲面中心の移動量を、背応力と呼びます。
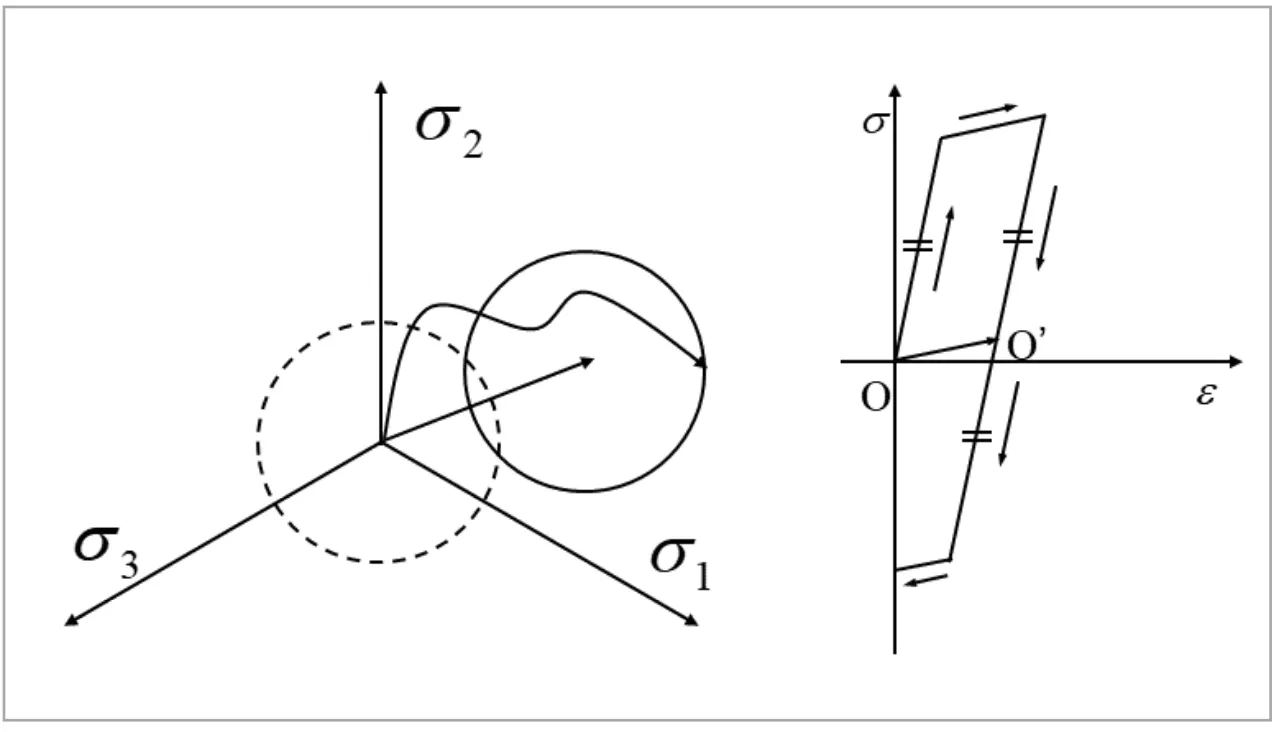
図3 移動硬化則
ここでも、単軸引張・圧縮状態を例として考えてみましょう。材料を単軸引張で![]() まで引っ張ったとき、降伏曲面は形と大きさを保持したまま、中心位置が引張方向へ
まで引っ張ったとき、降伏曲面は形と大きさを保持したまま、中心位置が引張方向へ![]() だけ移動します。中心の移動量
だけ移動します。中心の移動量![]() が背応力となります。この状態から除荷を行うと、降伏曲面の位置はそのままに、材料は弾性状態に戻ります。ここから、引張方向へ再負荷すると応力が
が背応力となります。この状態から除荷を行うと、降伏曲面の位置はそのままに、材料は弾性状態に戻ります。ここから、引張方向へ再負荷すると応力が![]() に達して初めて再降伏するのは、等方硬化則と同じです。しかし、除荷後に圧縮へと負荷方向を反転させる際の挙動は等方硬化則と異なります。降伏曲面の中心が
に達して初めて再降伏するのは、等方硬化則と同じです。しかし、除荷後に圧縮へと負荷方向を反転させる際の挙動は等方硬化則と異なります。降伏曲面の中心が![]() だけ引張側に移動していることから、圧縮の降伏応力は
だけ引張側に移動していることから、圧縮の降伏応力は![]() となります。これは
となります。これは![]() よりも大きい値となる(圧縮応力としてみれば、低い圧縮応力となる)ことがわかります。このように、移動硬化則を導入することで、Bauschinger効果を定性的に再現できることがわかります。しかし、移動硬化則を用いるとBauschinger効果を過大に評価する傾向にあること、また5.4.5の数値解析で示すように、一定ひずみ振幅での繰り返し負荷において降伏応力の上昇が全く見られないことなどが知られています。
よりも大きい値となる(圧縮応力としてみれば、低い圧縮応力となる)ことがわかります。このように、移動硬化則を導入することで、Bauschinger効果を定性的に再現できることがわかります。しかし、移動硬化則を用いるとBauschinger効果を過大に評価する傾向にあること、また5.4.5の数値解析で示すように、一定ひずみ振幅での繰り返し負荷において降伏応力の上昇が全く見られないことなどが知られています。
5.4.4 複合硬化則
弾性ひずみテンソル、そこで、等方硬化則と移動硬化則を組み合わせた複合硬化則が提案されています。複合硬化則では、塑性変形の進行とともに、降伏曲面の大きさと中心位置の両方が変化すると考えます。これにより、等方硬化則と移動硬化則の中間的な挙動を再現できることが期待されます。複合硬化則の概略を図4に示します。移動硬化則では、降伏曲面を超える応力の増加分が全て降伏曲面の中心の移動に費やされる、すなわち背応力が![]() で与えられました。複合硬化則では、応力の増加分は一部が降伏曲面の移動(背応力の増加)に、残りは降伏曲面の膨張に費やされると考えます。ここで、次式で定義される実効応力
で与えられました。複合硬化則では、応力の増加分は一部が降伏曲面の移動(背応力の増加)に、残りは降伏曲面の膨張に費やされると考えます。ここで、次式で定義される実効応力![]() を導入します。
を導入します。

応力![]() から背応力
から背応力![]() を引いた残りが実効応力となり、実効応力は移動した降伏曲面の中心を基準とした降伏曲面の大きさ(半径)を表しています。ここでは簡単のために1次元的に考えていますが、3次元の場合でも本質的な考え方は同じです。そして、応力の代わりに実効応力を用いて降伏関数を与えます。
を引いた残りが実効応力となり、実効応力は移動した降伏曲面の中心を基準とした降伏曲面の大きさ(半径)を表しています。ここでは簡単のために1次元的に考えていますが、3次元の場合でも本質的な考え方は同じです。そして、応力の代わりに実効応力を用いて降伏関数を与えます。

3次元的な応力状態でも、応力を実効応力に置き換えて降伏関数を定義すれば、第2回で紹介したMisesの降伏関数をはじめとする既存の降伏関数をそのまま用いて、複合硬化則を導入することができます。背応力の発展則としては、つぎの形式がよく用いられます。
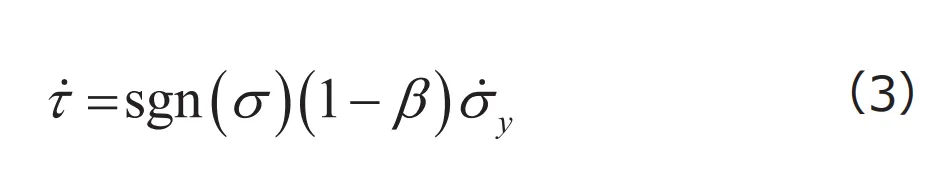
ここで![]() はカッコ内の値が正ならば
はカッコ内の値が正ならば![]() 、負ならば
、負ならば![]() を与える関数であり、上付きドットは時間微分を表しています。
を与える関数であり、上付きドットは時間微分を表しています。![]() は新たに導入されたパラメータであり、
は新たに導入されたパラメータであり、![]() の範囲をとります。この式は、降伏応力の微分(増分量)のうち、どれだけの割合が背応力の増分に寄与するかを表しています。
の範囲をとります。この式は、降伏応力の微分(増分量)のうち、どれだけの割合が背応力の増分に寄与するかを表しています。![]() ならば背応力は全く増減しない(常にゼロ)ことになり、これは等方硬化則に対応します。また
ならば背応力は全く増減しない(常にゼロ)ことになり、これは等方硬化則に対応します。また![]() ならば相当応力の増分は全て背応力の増分に費やされ、これは移動硬化則となります。そして、
ならば相当応力の増分は全て背応力の増分に費やされ、これは移動硬化則となります。そして、![]() を与えれば、両者の中間的な性質を持つ複合硬化則が得られることになります。
を与えれば、両者の中間的な性質を持つ複合硬化則が得られることになります。
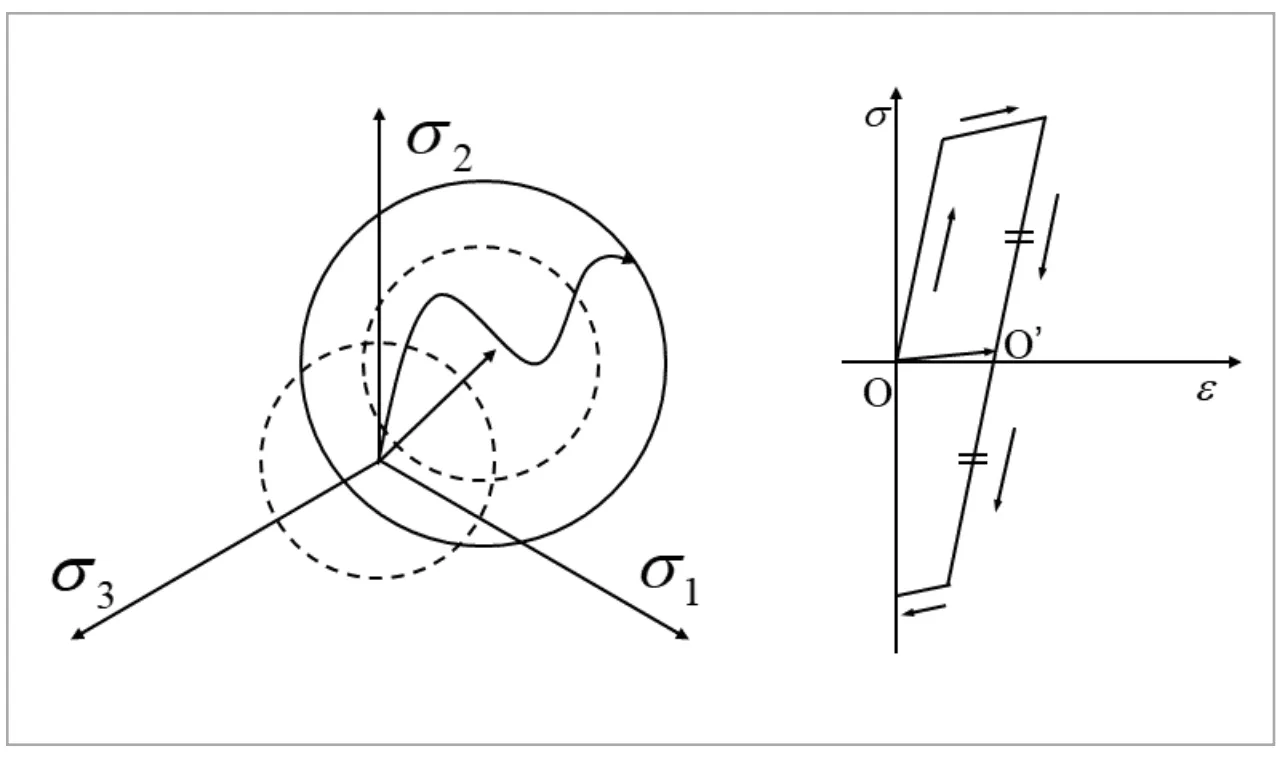
図4 複合硬化則
5.4.5 簡単な数値解析例
以上で紹介した等方硬化則、移動硬化則、複合硬化則の具体的なイメージを掴んで頂くために、簡単な数値解析例を紹介します。ここでは、例題としてひずみ制御および応力制御による繰り返し負荷解析を取り上げ、単軸引張・圧縮を繰り返し受ける材料を想定した弾塑性解析を実施します。ヤング率は200 GPa、初期降伏応力は200 MPa、初期降伏後のひずみ硬化係数は傾き2 GPaの一定値としています。
まず、ひずみ制御解析について見てみましょう。等方硬化則および移動硬化則を用いて、![]() の一定ひずみ振幅を繰り返し与えた場合の応力・ひずみ線図が、図5、6となります。図中には、1 サイクル目から10 サイクル目までの結果を示しています。等方硬化則を用いた場合(図5)には、サイクルを重ねる毎に引張、圧縮ともに降伏応力が上昇していくことがわかります。一方、移動硬化則を用いると(図6)、サイクルを重ねても応力・ひずみ挙動が全く変化していません(図中には1 サイクル目から10 サイクル目までの結果を図示していますが、完全に重なってしまっているため1 本の線に見えています)。これは、応力空間において降伏曲面が大きさを変えずに同じところを往復し続けており、サイクル毎の挙動に全く変化が生じないためです。
の一定ひずみ振幅を繰り返し与えた場合の応力・ひずみ線図が、図5、6となります。図中には、1 サイクル目から10 サイクル目までの結果を示しています。等方硬化則を用いた場合(図5)には、サイクルを重ねる毎に引張、圧縮ともに降伏応力が上昇していくことがわかります。一方、移動硬化則を用いると(図6)、サイクルを重ねても応力・ひずみ挙動が全く変化していません(図中には1 サイクル目から10 サイクル目までの結果を図示していますが、完全に重なってしまっているため1 本の線に見えています)。これは、応力空間において降伏曲面が大きさを変えずに同じところを往復し続けており、サイクル毎の挙動に全く変化が生じないためです。
等方硬化則では、サイクル毎に降伏応力が上昇していくことが表現されていました。そこで、横軸にサイクル数を、縦軸にサイクル毎の最大の降伏応力をプロットしたものを、図7に示します。ここでは複合硬化則も考え、式(3)のパラメータ![]() を1 から0 まで変化させています。また、サイクル数は300サイクルまで実施しました。移動硬化則(
を1 から0 まで変化させています。また、サイクル数は300サイクルまで実施しました。移動硬化則(![]() )の場合以外は、サイクル数の増加ともに降伏応力が増加していきますが、いずれの場合にもある一定の応力へと収束していく傾向が見てとれます。このように、繰り返し負荷に伴い降伏応力がある一定の応力へ収束する現象を、塑性シェイクダウンと呼びます。
)の場合以外は、サイクル数の増加ともに降伏応力が増加していきますが、いずれの場合にもある一定の応力へと収束していく傾向が見てとれます。このように、繰り返し負荷に伴い降伏応力がある一定の応力へ収束する現象を、塑性シェイクダウンと呼びます。![]() が大きいほど、少ないサイクル数で塑性シェイクダウンすることがわかります。ですから、この図に対応する実験結果と比較することで、パラメータ
が大きいほど、少ないサイクル数で塑性シェイクダウンすることがわかります。ですから、この図に対応する実験結果と比較することで、パラメータ![]() を決定することができます。
を決定することができます。
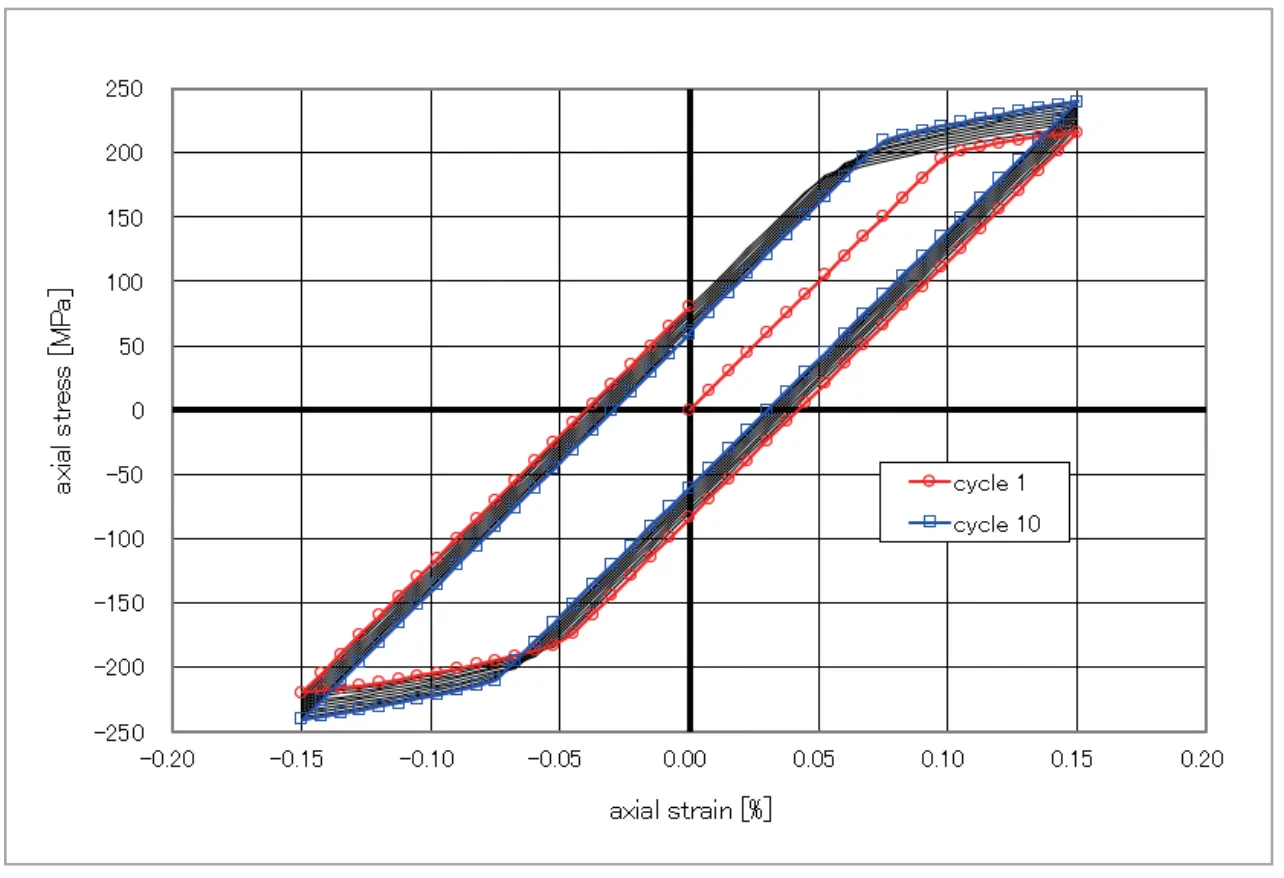
図5 等方硬化則によるひずみ制御解析
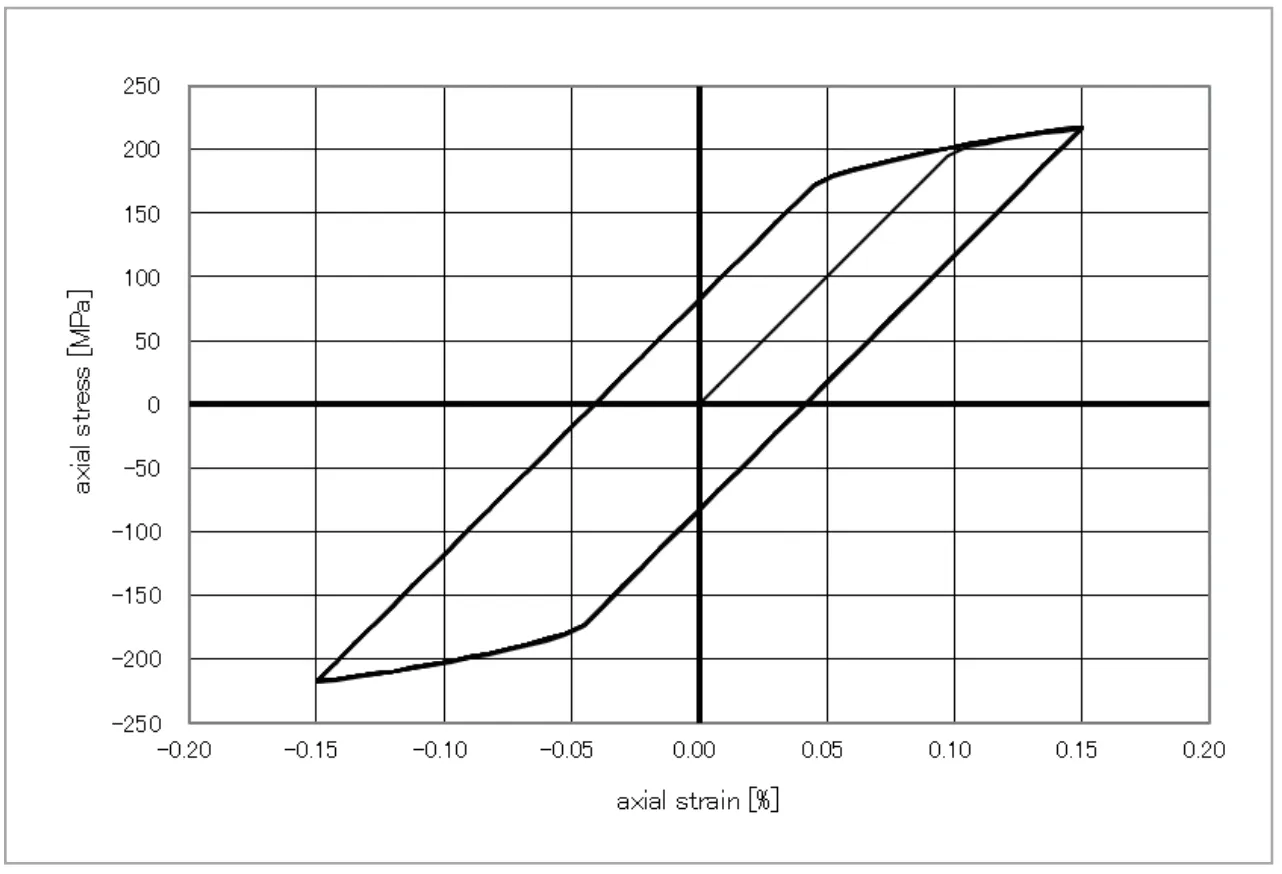
図6 移動硬化則によるひずみ制御解析 図
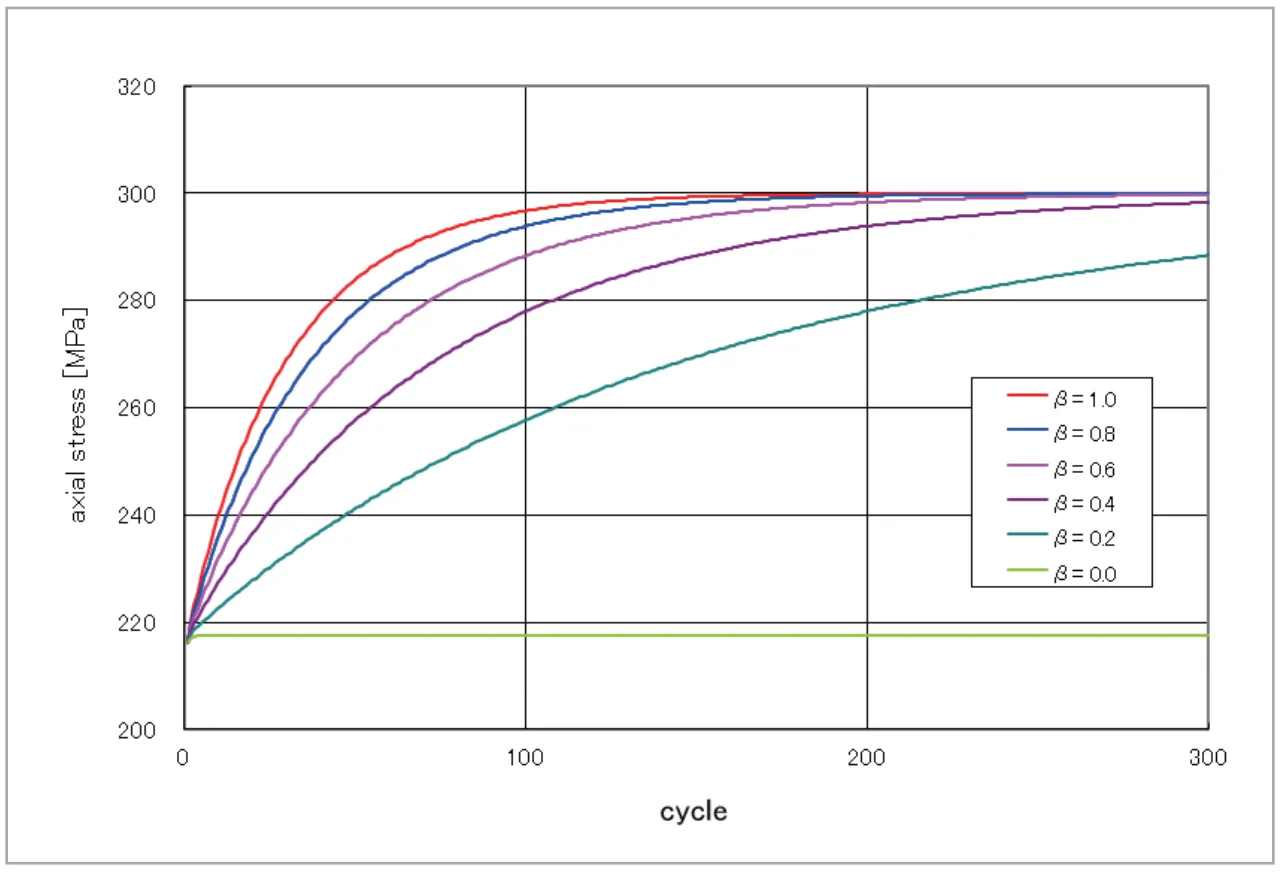
図7 塑性シェイクダウンの評価
つぎに、応力制御解析について考えます。ここでは、220 MPa から -200 MPa の応力振幅を繰り返し与えます。得られる応力・ひずみ線図(1サイクル~10サイクル)を図8、9に示しています。1サイクル終了する毎に応力がゼロに戻りますが、このとき塑性ひずみが発生しているため、ひずみはゼロになりません。結果として、サイクルを重ねる毎に応力・ひずみ線図が引張方向へ移動していく様子が確認できます。この現象をラチェッティング、累積していく塑性ひずみをラチェットひずみと呼びます。ラチェッティングは等方硬化則、移動硬化則、移動硬化則のどちらを用いても表現されますが、ラチェットひずみの累積量は硬化則によって異なることがわかります。
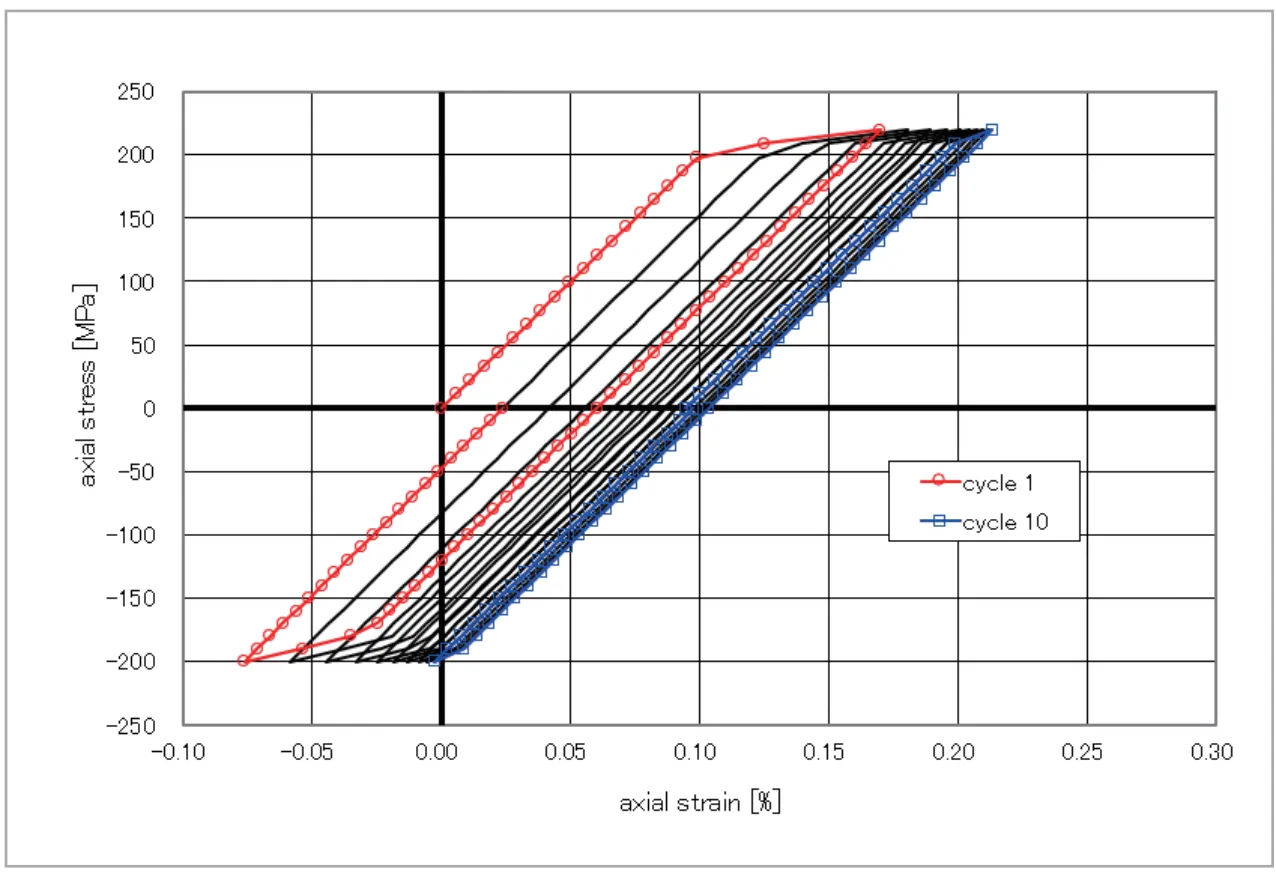
図8 等方硬化則による応力制御解析
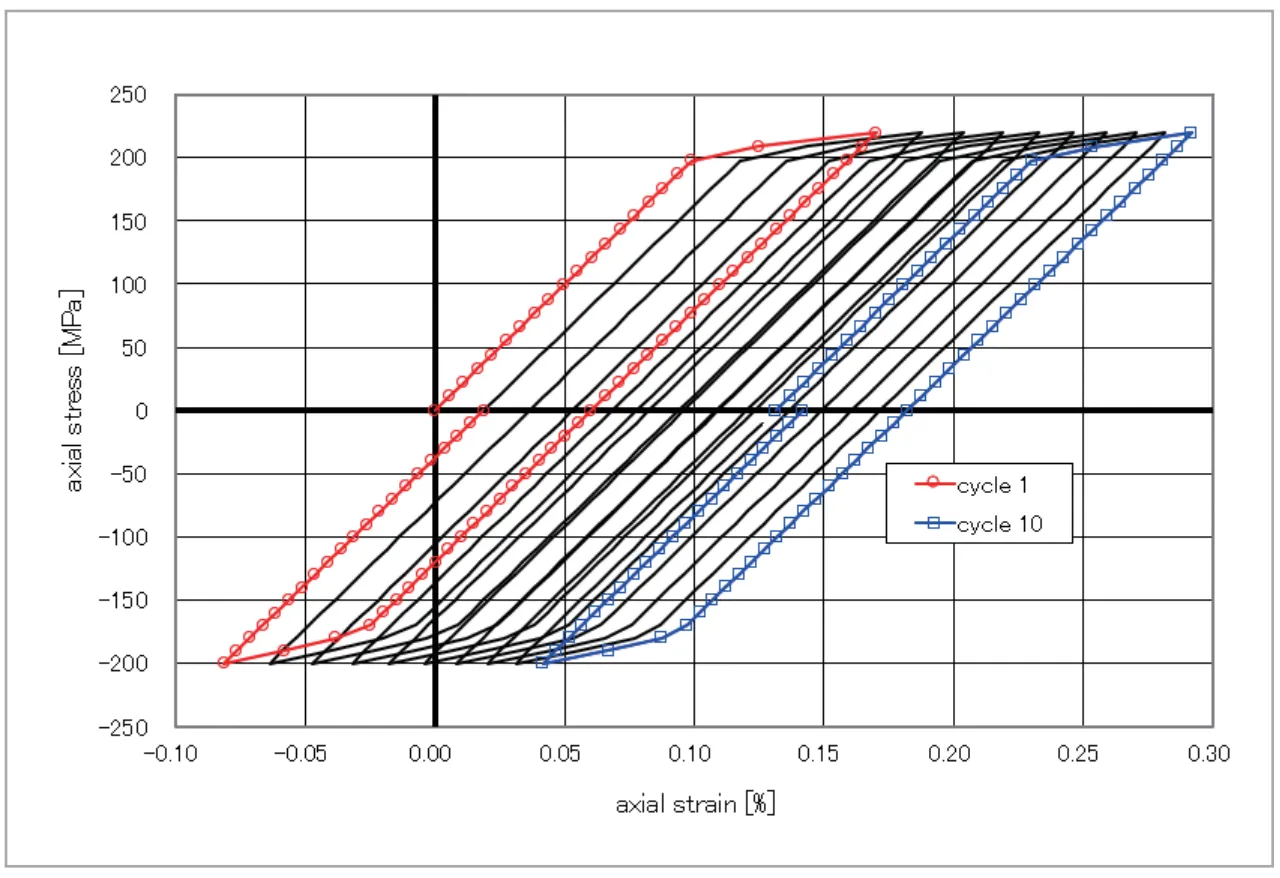
図9 移動硬化則による応力制御解析
複合硬化則を用いて得られるサイクル数とラチェットひずみの関係を、図10に示しています。はじめの数サイクルはラチェットひずみが![]() に依らず同じように累積していきますが、その後
に依らず同じように累積していきますが、その後![]() が大きいほど、早い段階でラチェットひずみが飽和する様子がわかります。すなわち、等方硬化則がラチェットひずみをも最も小さく、移動硬化則がラチェットひずみを最も大きく評価しています。ラチェットひずみは繰り返し負荷実験で実測可能ですから、そこからパラメータ
が大きいほど、早い段階でラチェットひずみが飽和する様子がわかります。すなわち、等方硬化則がラチェットひずみをも最も小さく、移動硬化則がラチェットひずみを最も大きく評価しています。ラチェットひずみは繰り返し負荷実験で実測可能ですから、そこからパラメータ![]() を同定することもできます。
を同定することもできます。
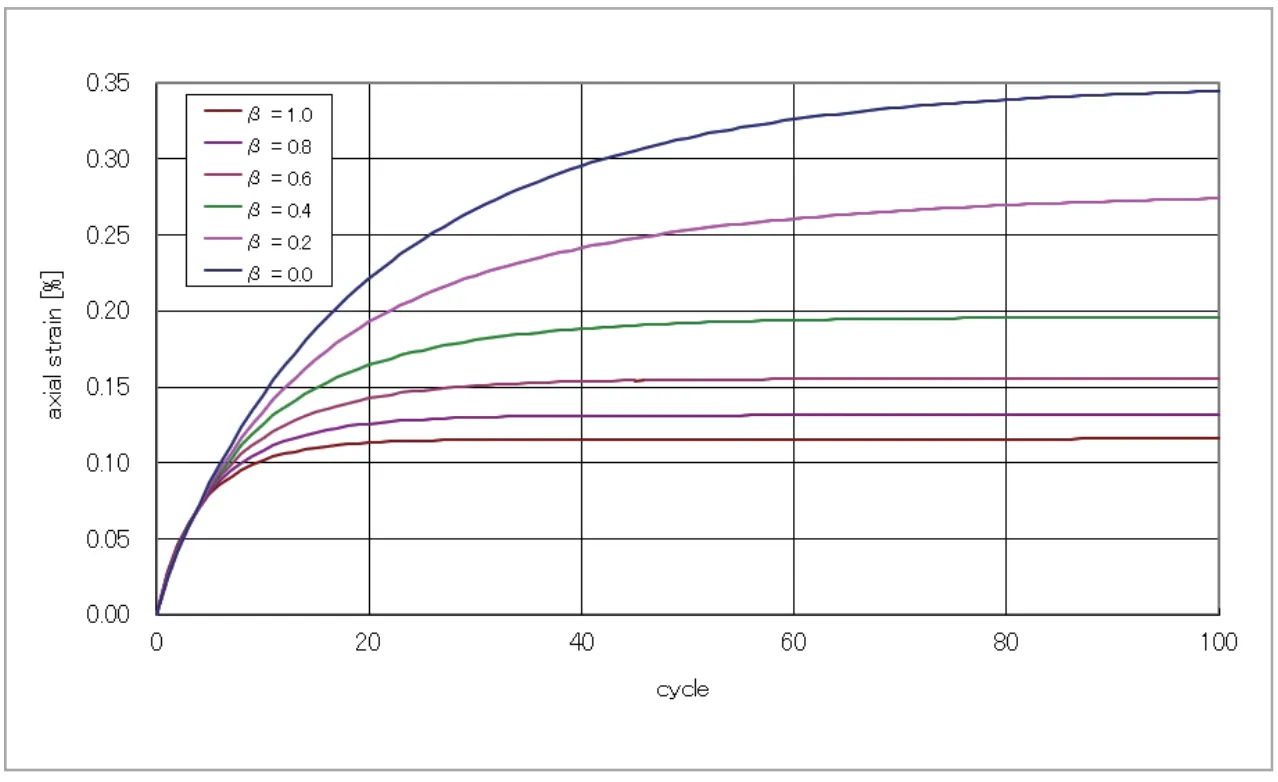
図10 ラチェッティングの評価
6 弾塑性構成式の基礎
以上で、弾塑性モデルを構築する際に必要な基礎知識を一通り解説しました。最後に、ここまでで解説した降伏関数やひずみ硬化則から、最終的な弾塑性構成式、すなわち応力とひずみの関係がどのように導出されるのかを概説します。
6.1 ひずみの加算分解と弾塑性構成式
第3回でも少し触れたように、弾塑性解析においては、一般に変形を弾性変形と塑性変形を分離して、それぞれについて構成式を考えます。ここでは、最もよく知られた方法の一つである、全ひずみが弾性ひずみと塑性ひずみの和に分解できる(加算分解)とする仮定を採用します。このとき、行列表示したひずみテンソル![]() は、つぎのように分解できます。
は、つぎのように分解できます。
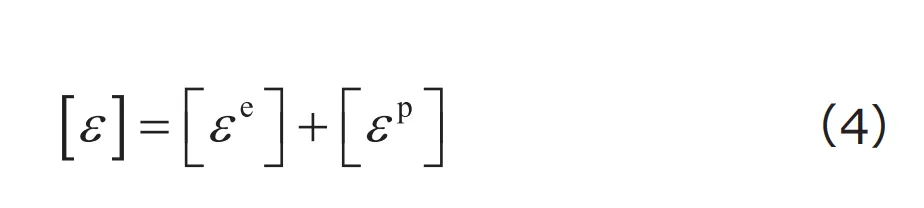
ここで![]() は、それぞれ行列表示した弾性ひずみテンソル、塑性ひずみテンソルです。このうち、弾性ひずみに対しては、弾性構成則が成り立つと仮定します。例えば、線形弾性体(フックの法則)を用いるのであれば、
は、それぞれ行列表示した弾性ひずみテンソル、塑性ひずみテンソルです。このうち、弾性ひずみに対しては、弾性構成則が成り立つと仮定します。例えば、線形弾性体(フックの法則)を用いるのであれば、

となります。ここで、![]() は弾性構成式を表す行列(3次元問題であれば
は弾性構成式を表す行列(3次元問題であれば![]() )、
)、![]() 、
、![]() は応力テンソルと弾性ひずみテンソルの独立成分(3次元問題であれば6つ)を並べたベクトルです。
は応力テンソルと弾性ひずみテンソルの独立成分(3次元問題であれば6つ)を並べたベクトルです。
弾塑性問題では、一般に応力・ひずみ関係が負荷経路に依存するため、応力とひずみの関係の代わりに、ある瞬間における応力速度(応力増分)とひずみ速度(ひずみ増分)の関係を考えます。そこで、式(5)の両辺を時間微分し、さらに式(4)の両辺を時間微分したものを代入することで、次式が得られます。
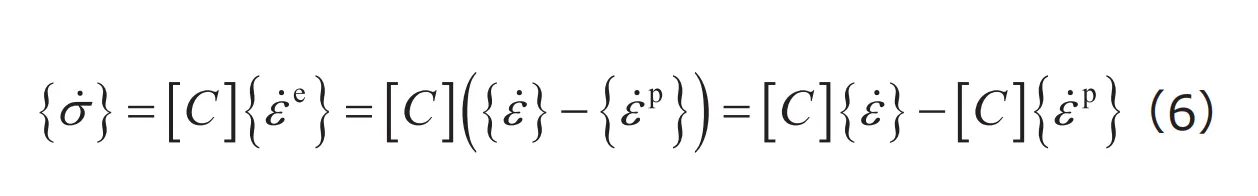
すなわち、弾性構成式が与えられていれば、あとは塑性ひずみ速度に対する構成式を定義することで、弾塑性構成式を定義できることになります。なお、全ひずみ速度と応力速度が既知なのであれば、式(6)より、塑性ひずみ速度はつぎのように計算できます
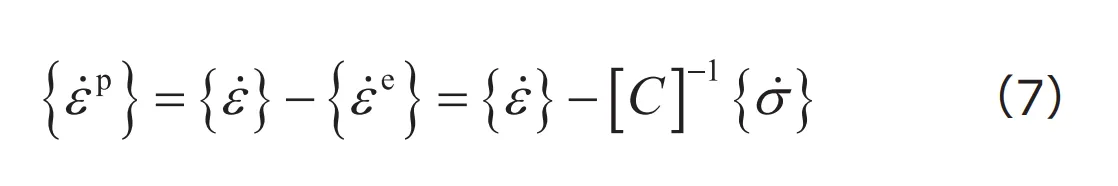
また、塑性ひずみ速度テンソルの各成分から、相当塑性ひずみ速度が次式で定義されます。
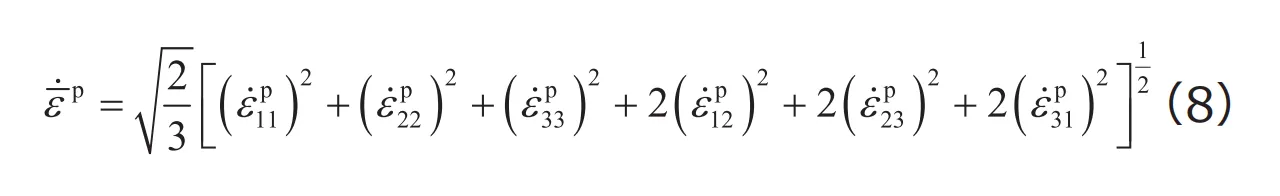
前回紹介した相当応力と相当塑性ひずみの関係を表すひずみ硬化則を3次元問題で考える際には、上式を変形を通じて積分することで得られる相当塑性ひずみを用いることになります。
6.2 関連流れ則
前述の通り、弾塑性構成式を考える際には、塑性ひずみ速度の構成式を定義する必要があります。これには色々なモデルが提案されていますが、その中でも代表的なものの一つが、降伏関数![]() を応力で微分したものが塑性ひずみ速度の方向と一致すると仮定するモデルです(降伏関数は応力の関数となることを思い出しましょう)。これを関連流れ則と呼びます。すなわち、塑性ひずみ速度が次式で与えられます。
を応力で微分したものが塑性ひずみ速度の方向と一致すると仮定するモデルです(降伏関数は応力の関数となることを思い出しましょう)。これを関連流れ則と呼びます。すなわち、塑性ひずみ速度が次式で与えられます。

![]() は発生する塑性ひずみ速度の大きさを表す係数です。降伏関数を応力で微分すると、応力空間における降伏曲面の法線方向が得られることから、関連流れ則は降伏曲面の法線方向に塑性ひずみ速度が発生するという考え方になります。実験的にも、多くの塑性変形は関連流れ則に従って生じることが知られており、今日最も広く用いられている弾塑性構成式となります。関連流れ則において、降伏関数は任意に選択することができますが、降伏曲面の法線方向によって塑性ひずみ速度の方向が決まることから、降伏関数は塑性変形の生じ方に大きな影響を及ぼします。このことから、降伏関数は材料がいつ降伏するかを表すだけでなく、塑性変形がどのように発生するかを表現する際にも重要な役割を果たすことがわかります。
は発生する塑性ひずみ速度の大きさを表す係数です。降伏関数を応力で微分すると、応力空間における降伏曲面の法線方向が得られることから、関連流れ則は降伏曲面の法線方向に塑性ひずみ速度が発生するという考え方になります。実験的にも、多くの塑性変形は関連流れ則に従って生じることが知られており、今日最も広く用いられている弾塑性構成式となります。関連流れ則において、降伏関数は任意に選択することができますが、降伏曲面の法線方向によって塑性ひずみ速度の方向が決まることから、降伏関数は塑性変形の生じ方に大きな影響を及ぼします。このことから、降伏関数は材料がいつ降伏するかを表すだけでなく、塑性変形がどのように発生するかを表現する際にも重要な役割を果たすことがわかります。
Misesの降伏関数を用いた関連流れ則を、特に![]() 流れ則と呼ぶことがあり、多くの汎用ソフトウェアで標準の弾塑性モデルとして導入されています。式(9)の降伏関数 に第2回で紹介したMisesの降伏関数を代入すると、最終的に次式が得られます。
流れ則と呼ぶことがあり、多くの汎用ソフトウェアで標準の弾塑性モデルとして導入されています。式(9)の降伏関数 に第2回で紹介したMisesの降伏関数を代入すると、最終的に次式が得られます。
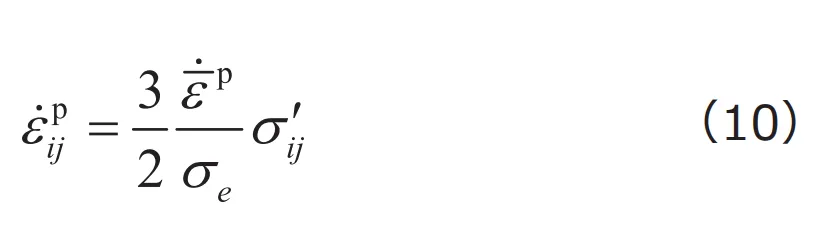
![]() は偏差応力、
は偏差応力、![]() はMisesの相当応力です。
はMisesの相当応力です。![]() 流れ則においては、塑性ひずみ速度は偏差応力と同じ方向に生じることがわかります。式(6)に式(10)を代入し、いくつかの式変形を経ると、応力速度と全ひずみ速度の関係が最終的につぎのように得られます。
流れ則においては、塑性ひずみ速度は偏差応力と同じ方向に生じることがわかります。式(6)に式(10)を代入し、いくつかの式変形を経ると、応力速度と全ひずみ速度の関係が最終的につぎのように得られます。
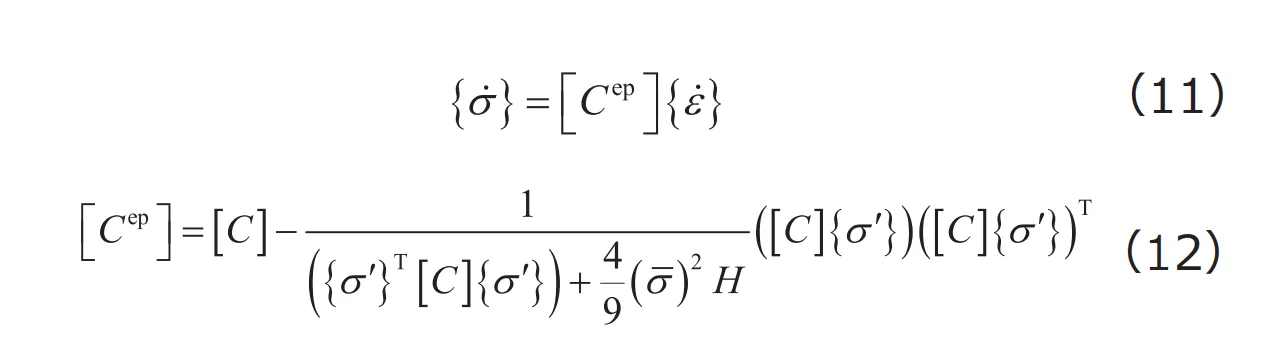
ここで、![]() は第3回で示した相当応力・相当ひずみ関係の傾きであり、
は第3回で示した相当応力・相当ひずみ関係の傾きであり、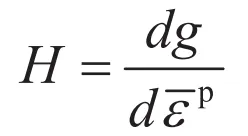 で与えられます。ですから、ひずみ硬化則が同定されれば式(11)、(12)の具体形が決定され、弾塑性構成式が与えられることになります。
で与えられます。ですから、ひずみ硬化則が同定されれば式(11)、(12)の具体形が決定され、弾塑性構成式が与えられることになります。
7 おわりに
本稿では、4回に渡って弾塑性材料モデルの基礎について解説しました。弾塑性変形は極めて複雑な非線形材料挙動であり、既存のモデルでは十分に表現できない現象も多数残されています。このため、より高精度な材料モデリングに関する研究が、今日でも精力的に続けられています。
一方で、基本的な弾塑性変形であれば、本稿で紹介した古典的モデルでも十分に評価できることは少なくありません。また、より高度な弾塑性モデルを利用するにあたっても、その基盤となっているのは古典的弾塑性モデルですから、古典的な弾塑性モデルを理解していなければ、最新の弾塑性モデルを理解し効果的に使うこともままなりません。本稿が、弾塑性材料モデルの基礎を正しく理解し、CAEによる弾塑性解析を有効活用するための一助になるのであれば幸いです。
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

【全記事】CAEのあるものづくり vol.42
ユーザー様インタビュー記事7件を1冊に集約した保存版
-

誤差との上手なつきあい方 ~流体解析の計算誤差~ (完全保存版)
誤差との上手なつきあい方 前編・後編 を1冊にまとめた保存版 PDF
-

非線形解析の壁を突破するシミュレーション技術
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

共振回避だけで終わらせない実レベルの振動解析
~Ansys Mechanicalで実現する高度な製品開発~
-
吸入器内の粒子挙動を可視化する
~薬剤送達効率向上に向けた解析~