CAEを学ぶ
ミーゼス応力をどう説明するか?
ミーゼス応力をどう説明するか?の概要

1 はじめに
そこで本稿では、ミーゼス応力の意味や、垂直応力・せん断応力と比べたミーゼス応力の優位性、そして主応力やトレスカ応力との違いや注意点を解説します。
2 ミーゼス応力とはどんな応力なのか?
ミーゼス応力は、材料の降伏理論の1つであるせん断ひずみエネルギー説(ミーゼス応力説)に基づいています。この説ではミーゼス応力![]() が降伏応力
が降伏応力![]() に達すると塑性を開始すると考えます。延性材料によく適合することが知られています。
に達すると塑性を開始すると考えます。延性材料によく適合することが知られています。
したがって端的に説明すれば「ミーゼス応力とは延性材料の降伏予測に適した判定基準」となります。もう少し踏み込めば「延性材料の降伏応力に相当するように計算して求めた判定基準」となります。ミーゼス応力が一般に「相当応力」と呼ばれる所以です。
2.1 まずはミーゼス応力の定義を確認
ミーゼス応力![]() は主応力(
は主応力(![]() 詳細後述)で表すと(式1)、垂直応力とせん断応力で表すと(式2)のようになります。式に表されているとおり、ミーゼス応力は方向を持たないスカラー量であり、正負の区別がありません。
詳細後述)で表すと(式1)、垂直応力とせん断応力で表すと(式2)のようになります。式に表されているとおり、ミーゼス応力は方向を持たないスカラー量であり、正負の区別がありません。
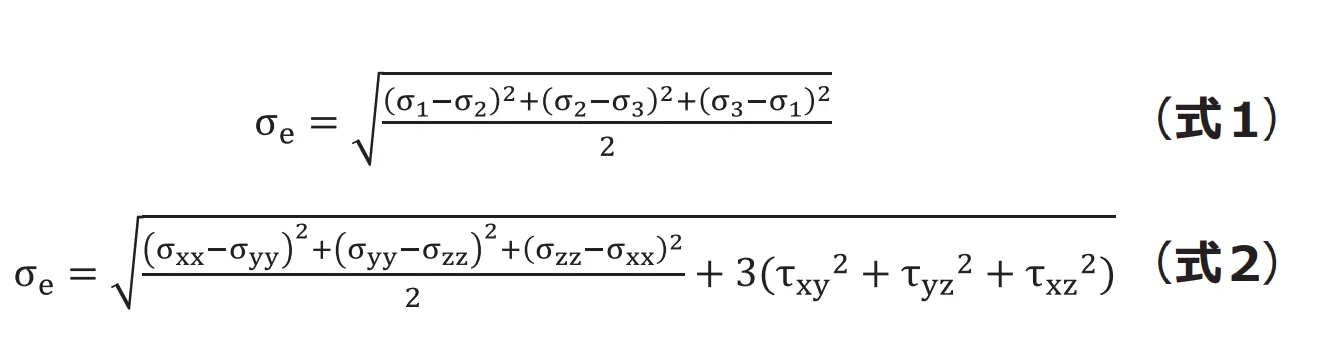
(式1)をみると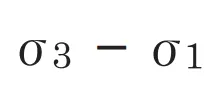 のように主応力を引き算しています。モールの応力円(図1)に示すように、主応力の引き算はせん断応力の2倍にあたるので、ミーゼス応力はせん断応力に関連していることが推察できます。
のように主応力を引き算しています。モールの応力円(図1)に示すように、主応力の引き算はせん断応力の2倍にあたるので、ミーゼス応力はせん断応力に関連していることが推察できます。
詳細な説明は省きますが、ミーゼス応力は材料降伏が始まるときに働くせん断作用の大きさを、一軸引張の降伏応力に相当するように対応させた応力であるとお考えください。(詳細は参考文献[1]の「第2 章 コーシー応力」をご覧ください)
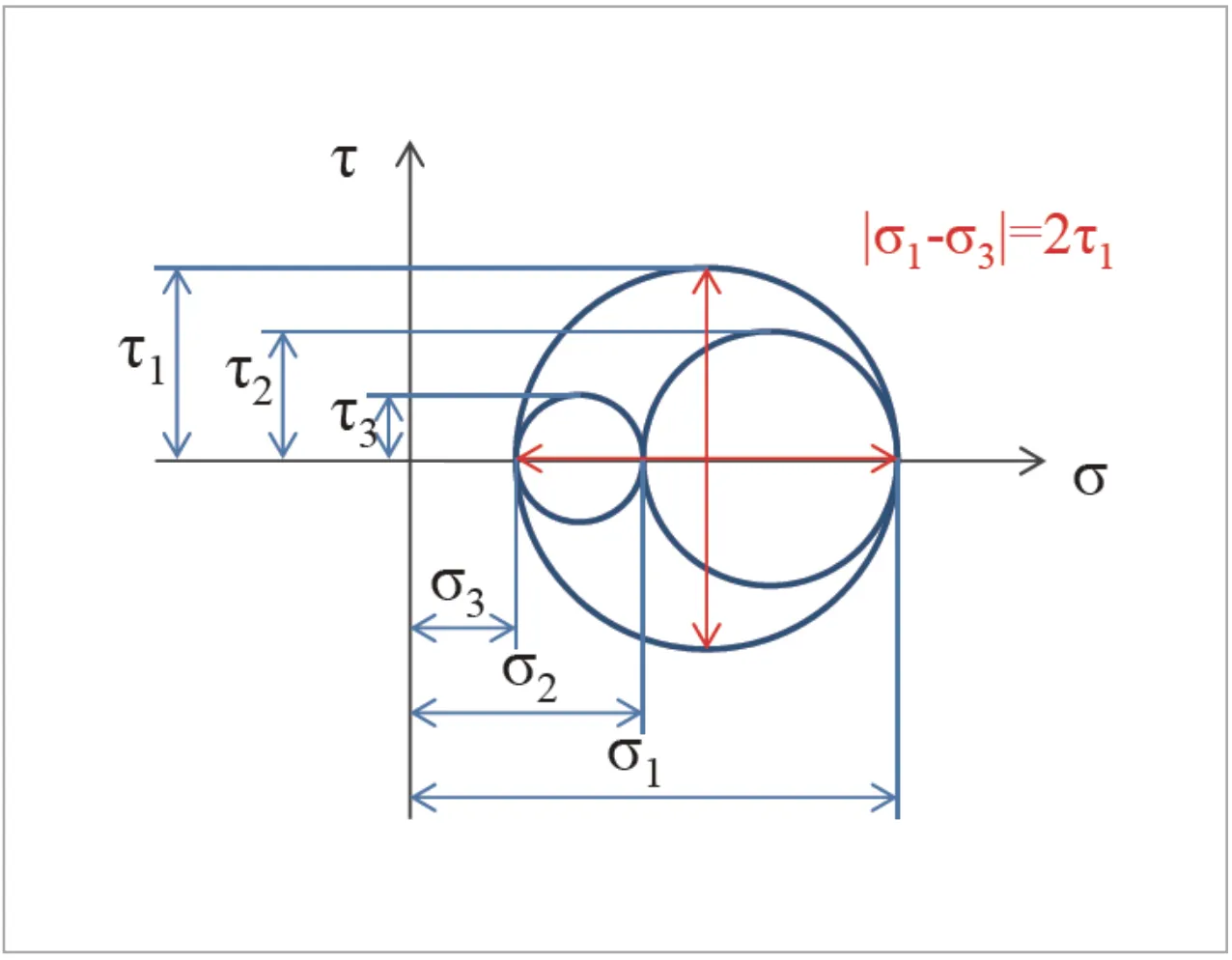
図1 モールの応力円
2.2 ミーゼス応力の性質
ミーゼス応力は、![]() (定数)として主応力空間で図示すると、
(定数)として主応力空間で図示すると、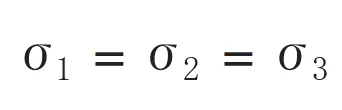 を中心軸とする半径 の円筒表面になり、これが塑性材料におけるミーゼスの降伏条件を表しています。円筒の内側は弾性の領域、外側が塑性の領域になります。(図2)
を中心軸とする半径 の円筒表面になり、これが塑性材料におけるミーゼスの降伏条件を表しています。円筒の内側は弾性の領域、外側が塑性の領域になります。(図2)
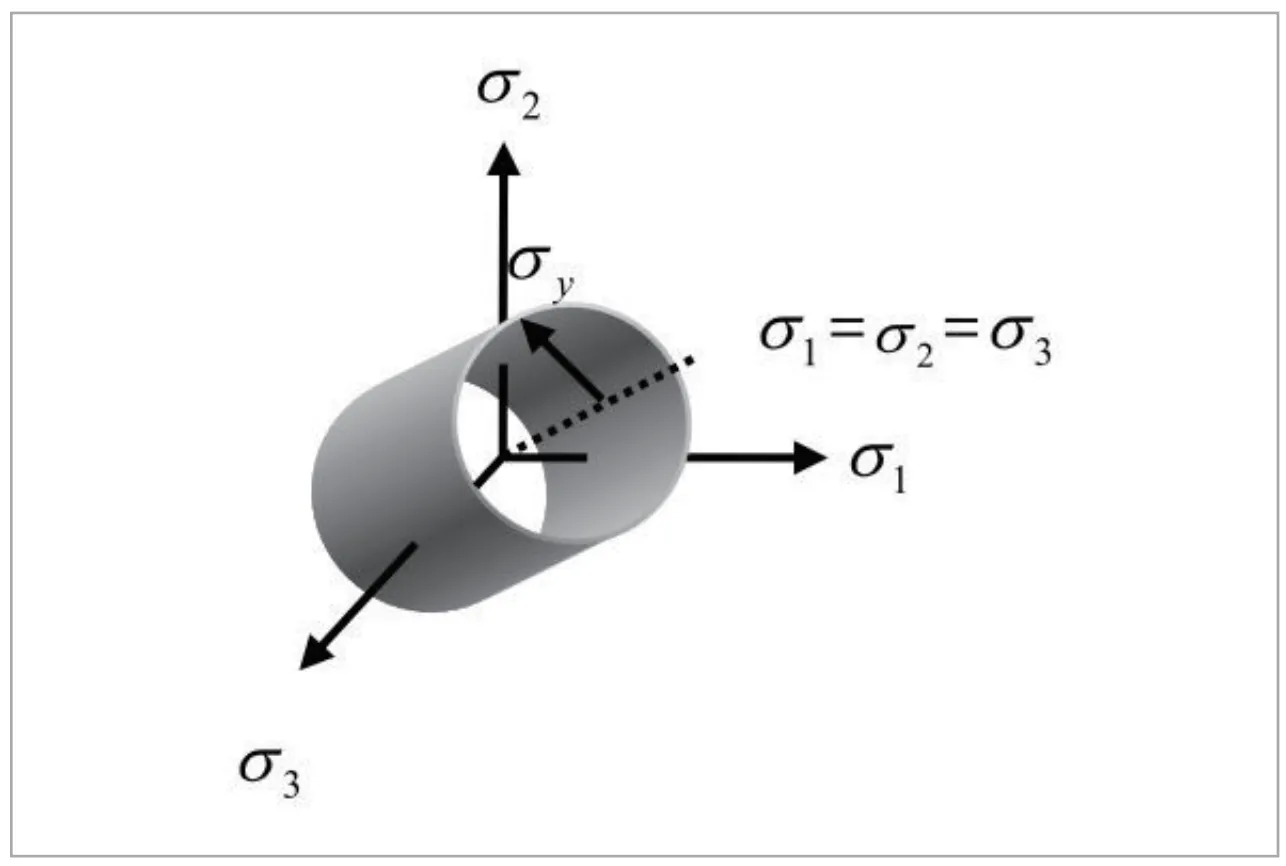
図2 ミーゼスの降伏曲面
もし応力状態が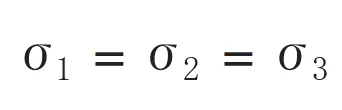 ならば全方向から同じ力を受ける、つまり平均応力(静水圧)がかかっていることを示します。ミーゼスの降伏条件では静水圧をどれだけかけても、それだけでは材料は降伏しません。ミーゼス応力は単純に応力の大小を見るものではないことがわかります。
ならば全方向から同じ力を受ける、つまり平均応力(静水圧)がかかっていることを示します。ミーゼスの降伏条件では静水圧をどれだけかけても、それだけでは材料は降伏しません。ミーゼス応力は単純に応力の大小を見るものではないことがわかります。
2.3 ミーゼス応力の優位性
2.4 ミーゼス応力の注意点
たとえば疲労破壊は引張応力下で促進されるため、引張応力が働く箇所を集中的に対策する必要がありますが、ミーゼス応力だけでは対策すべき箇所を判断できないことになります。(このような場合は主応力もあわせて観察することをお勧めします)
2.5 ミーゼス応力は万能では無い
3 垂直応力・せん断応力
3.1 垂直応力
まず物体中に任意の直交座標を定義し、その座標軸を法線方向とする微小な立方体領域を仮定します。この微小立方体が外力を受けているときの単位面積あたりの内力を垂直応力と呼びます。ここでは添え字の1番目は作用面の法線方向を、2番目は応力の作用方向を表すようにして、Y方向の垂直応力を![]() と記載します。(図3)
と記載します。(図3)
※細かく言えば、割り算に使用する面積を変形後と変形前のどちらにするかで違いが生じるのですが、ここでは両者にほぼ差がない微小変形状態を仮定しています
同様にして、他の面についても考えると、面の法線方向に働く応力は合計3成分( 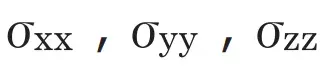 )存在することになります。
)存在することになります。
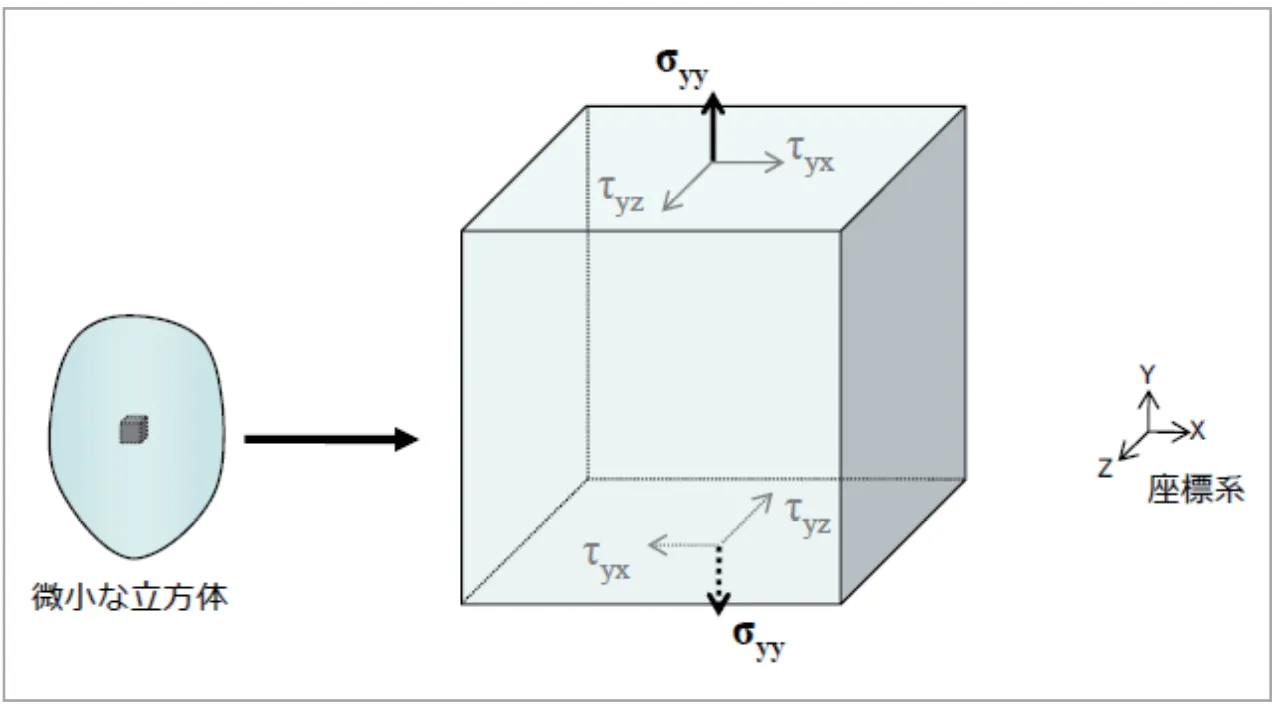
図3 Y方向垂直応力
3.2 せん断応力
立方体が斜めにずれるような外力を受けたときに発生する、単位面積あたりの内力をせん断応力と呼びます。垂直応力と同様に、せん断(接線方向)の向きを添え字に記載します。![]() であればY 軸に垂直な微小面にZ方向の向きになります。(図4)
であればY 軸に垂直な微小面にZ方向の向きになります。(図4)
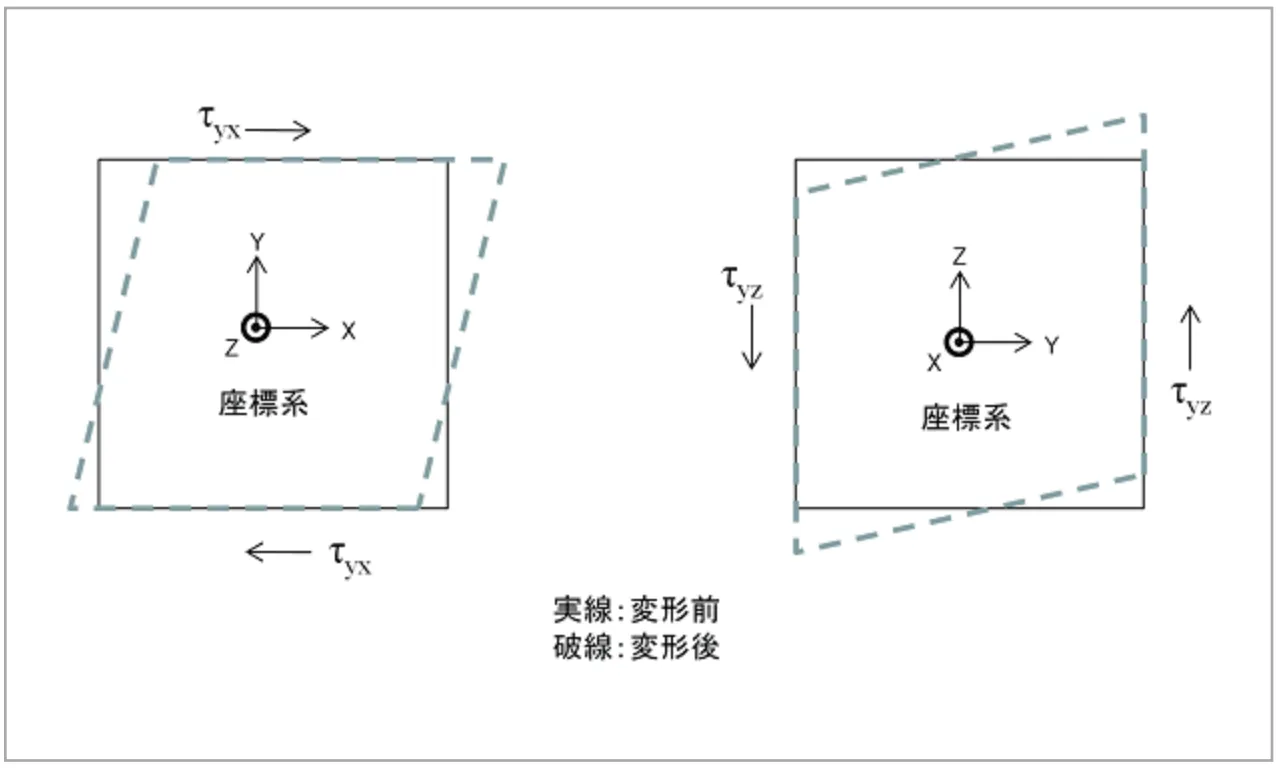
図4 YX方向およびYZ方向せん断応力
同様にして他の面についても考えると、面の接線方向に働く応力は合計6 成分存在することになりますが、YX面内のモーメントの釣り合いにより![]() となります。
となります。
同様に であるため、面の接線方向に働く独立な応力成分は全部で3 つになります。(図5)
であるため、面の接線方向に働く独立な応力成分は全部で3 つになります。(図5)
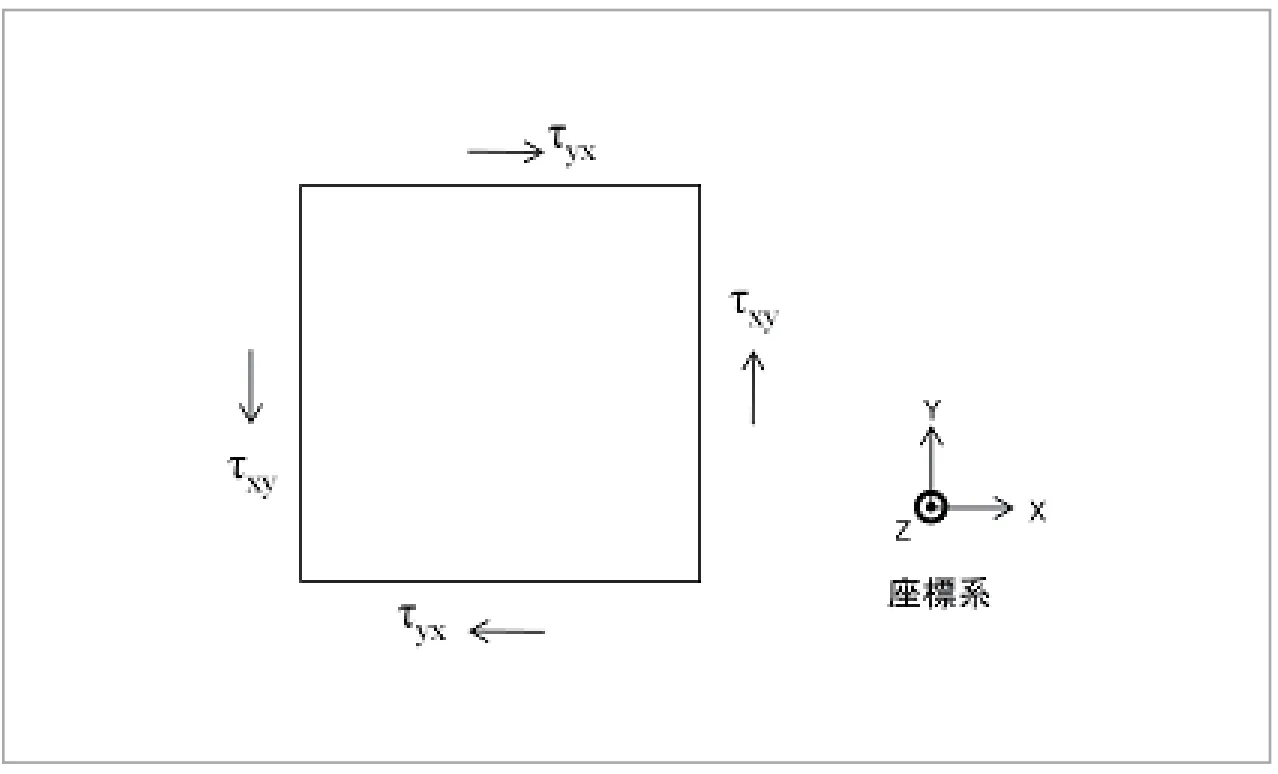
図5 モーメントの釣り合い
3.3 応力テンソル
これらの垂直応力とせん断応力を組み合わせれば、微小立方体が様々な変形をしたときに受けている力を表現できます。そこで応力を添え字に注意してマトリクスの形にひとまとめで表記してみます。これを応力テンソルと呼びます。(本稿ではテンソルについて詳しくは触れません。ご興味のある方は参考文献[1]等をご覧ください)
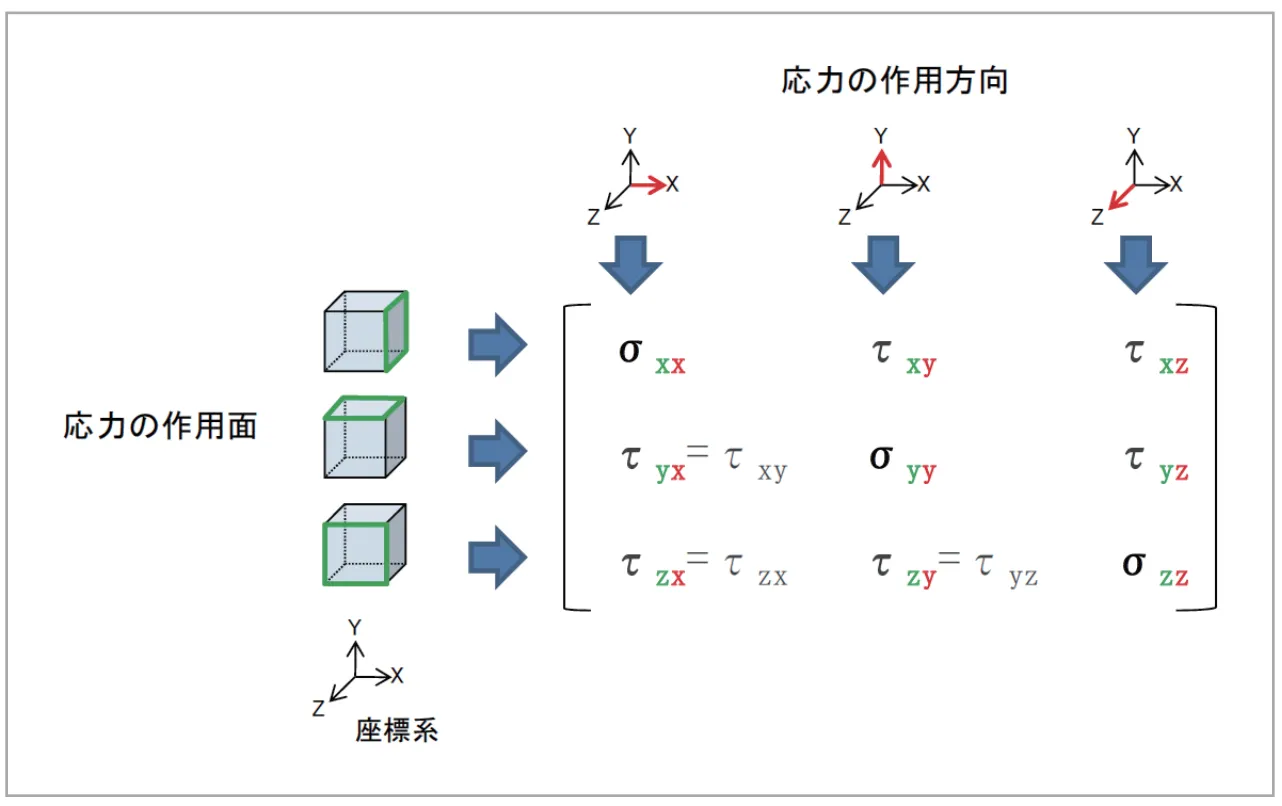
図6 応力テンソル
3.4 垂直応力とせん断応力の使い道
3.5 垂直応力とせん断応力の不便な点
3.5.1 不便な点(1):6 成分もある
1 つ目は成分が6個もあることです。あまり使われていませんが、CAEソフトには6成分すべての値を出力する機能が備わっています。試しに適当な解析データで、基準座標系を全体座標系として出力してみます。(図7)に示したとおり、ちゃんと6 成分出力できています。ただ、この6個の値を見ただけでは、X方向に強い力が働いてそうなことぐらいは把握できますが、強度評価するのは容易ではありません。

図7 垂直応力・せん断応力結果例
3.5.2 不便な点(2):基準座標系により結果が変わる
2つ目はモデルの向きや基準となる座標系により結果が変わることです。(図8)に示すような単純な棒に軸方向の力を加えて引っ張った結果を見てみます。ここでは軸方向が全体座標系X 軸に向いており、さらにX軸方向の応力が他の成分より卓越していますので、X軸垂直応力を見れば強度評価できそうです。
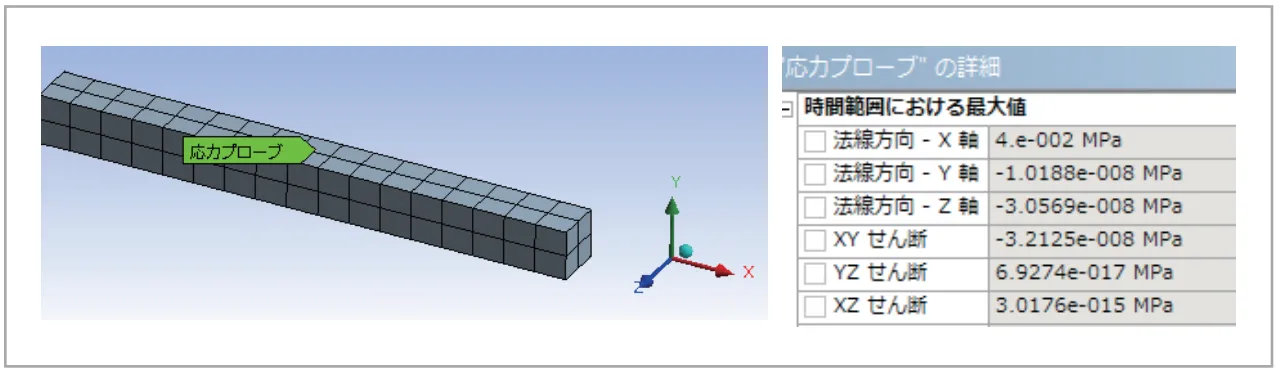
図8 全体座標系を基準とした応力結果例1
次に棒を荷重の方向も含めて丸ごと45度傾けてみます。かかる力は同じですが、応力結果はX,Y垂直応力に加えXYせん断応力も出てくるため一気に複雑になってしまいました(図9)。このように垂直応力・せん断応力はモデルの向き(または基準座標系)が変わると、力の状態は同じでも見かけの結果が変わってしまうため注意が必要です。
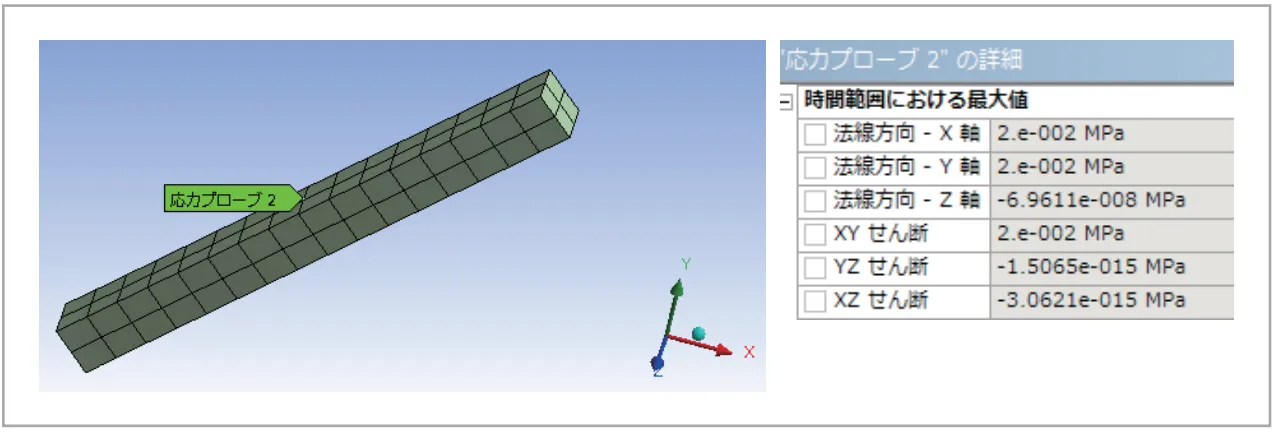
図9 全体座標系を基準とした応力結果例2
このままではわかりづらいので、棒の軸方向に向けた局所座標系を作成し、これを基準に応力結果を出力すれば傾ける前と同じ状態になり、わかりやすくなります(図10)。
しかし、いちいち局所座標系を作るのは手間がかかりすぎ非現実的です。
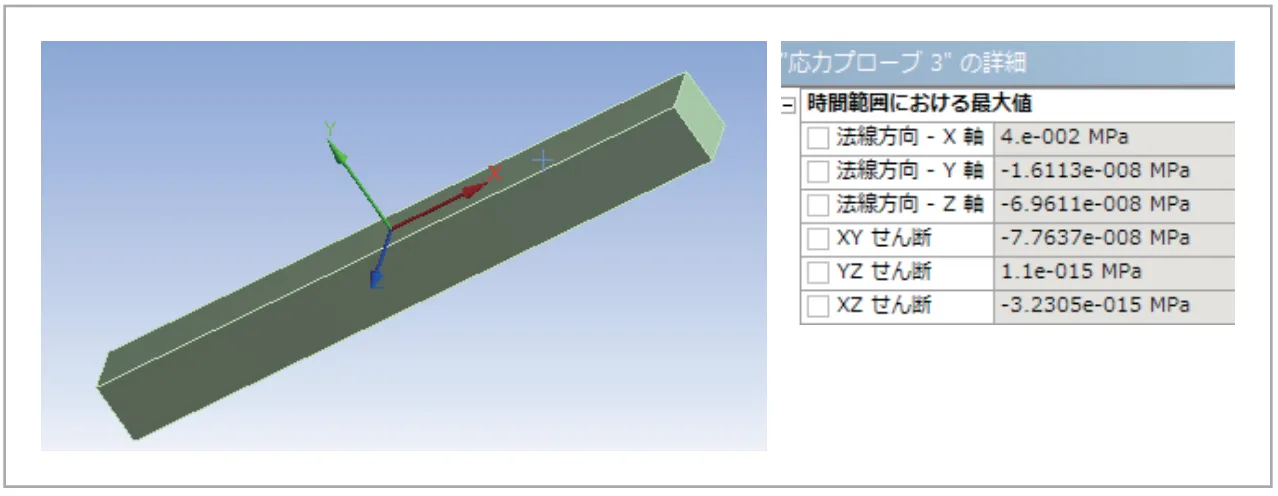
図10 棒の軸方向を基準とした応力結果例
そこで登場するのが、主応力やトレスカ応力、そしてミーゼス応力です。
4 主応力
先の例で基準となる座標系を変えると、せん断成分がゼロとなって評価しやすくなることを示しました。これと同じような考え方で、物体中の微小な立方体を回転させると、どのような荷重状態でもせん断成分がゼロとなる軸方向が存在することが知られています。
少し難しい話になりますが、応力テンソルは3×3の対称行列なので、数学的な性質により![]() を満足する固有値
を満足する固有値![]() が3つ存在し、それぞれの固有方向は直交することで説明できます。応力テンソル
が3つ存在し、それぞれの固有方向は直交することで説明できます。応力テンソル![]() の固有方向を主軸とする座標系で表すと(式3)のような対角行列となり、せん断成分はゼロになります。(詳細は参考文献[1]をご覧ください)
の固有方向を主軸とする座標系で表すと(式3)のような対角行列となり、せん断成分はゼロになります。(詳細は参考文献[1]をご覧ください)
主応力と同じような考え方で、物体中の
ここで![]() を主応力(Principal Stress)と呼びます。互いに直交する三方向から押されたり、引っ張られたりしている状態を表しています。(図11)
を主応力(Principal Stress)と呼びます。互いに直交する三方向から押されたり、引っ張られたりしている状態を表しています。(図11)
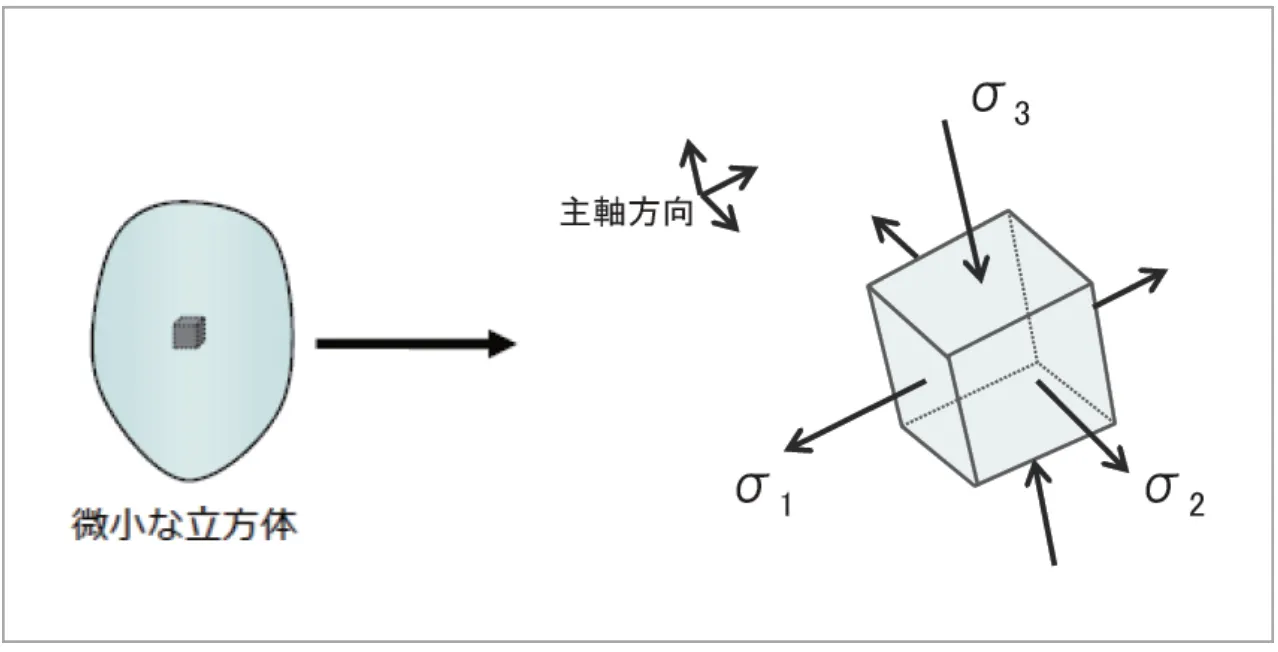
図11 主応力
4.1 主応力の便利な点
6成分ある垂直応力・せん断応力に比べて主応力は3成分しかありません。しかもせん断成分がないため、力が生じている方向がわかりやすいのが特徴です。モデルの向き(もしくは基準座標系)によって値が変化しないので便利です。
(図12)は左端固定で右端に長手方向の引張力を負荷したときの最大主応力図です。モデルを回転させても結果が変わらないことがわかります。
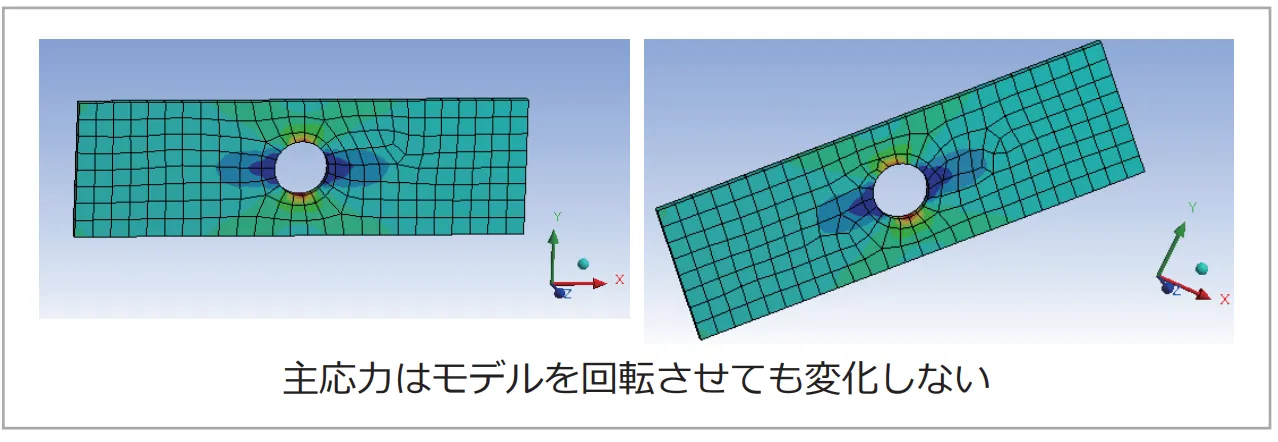
図12 最大主応力結果表示例
(図13)のように主応力ベクトル(主軸方向)を表示すれば、力のかかる方向を見ることもできます。ここでは赤色が最大主応力、青色が最小主応力で、矢印が長いほど強い応力が働くことを示します。これは方向性を持たないミーゼス応力には不可能な芸当で、主応力を利用する大きなメリットの1 つです。
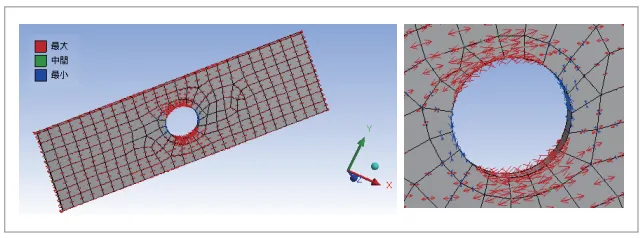
図13 主応力ベクトル結果表示例
4.2 主応力は万能か?
そこで、せん断成分に注目したのが、最大せん断応力やトレスカ応力、そしてミーゼス応力です。
5 最大せん断応力とトレスカ応力 (応力強さ)
主応力と同じような考え方で、物体中の微小な立方体を、せん断応力が最大になるように回転させてみます。このとき現れるせん断応力3成分を主せん断応力と呼び、最大のものを最大せん断応(Max Shear Stress)と呼びます。最大せん断応力![]() は主応力を用いて(式4)のように表されます。(ここで
は主応力を用いて(式4)のように表されます。(ここで![]() :最大主応力、
:最大主応力、![]() :最小主応力)
:最小主応力)

5.1 最大せん断応力の強度評価への利用
引張り試験で得られる降伏応力![]() と最大せん断応力の関係を考えてみます。一軸の引張り試験では
と最大せん断応力の関係を考えてみます。一軸の引張り試験では![]() =
=![]() 、
、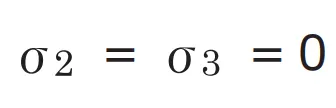 であるため(式5)のようになります。が の1/2 に達すると降伏するとみなして、強度評価に利用できます。
であるため(式5)のようになります。が の1/2 に達すると降伏するとみなして、強度評価に利用できます。
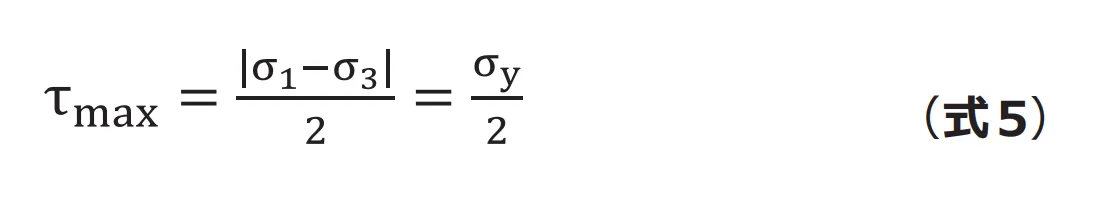
5.2 トレスカ応力(応力強さ)
さらに使いやすくしたのがトレスカ応力(Tresca Stress)です。応力強さ(Stress Intensity)とも呼びます。トレスカ応力![]() は(式6)で表されるとおり最大せん断応力の2倍になります。
は(式6)で表されるとおり最大せん断応力の2倍になります。
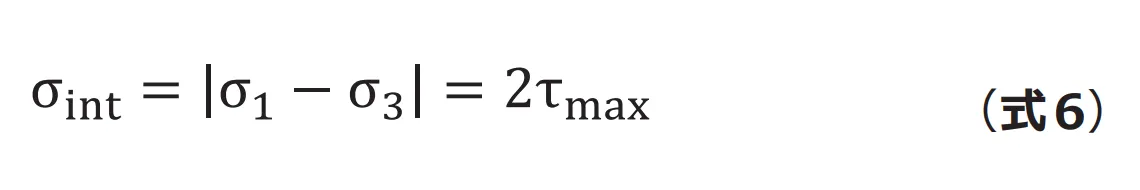
トレスカ応力![]() が
が![]() に達すると塑性を開始するとみなせます。これが材料の降伏理論の1 つである最大せん断応力説(トレスカ応力説)です。
に達すると塑性を開始するとみなせます。これが材料の降伏理論の1 つである最大せん断応力説(トレスカ応力説)です。
トレスカ応力は応力状態を1つの値で表現でき、材料の降伏応力と見比べるだけで延性材料の降伏予測ができます。
5.3 なぜトレスカ応力は使われないのか?
トレスカ応力はミーゼス応力とよく似ていますが、CAEを利用した強度評価ではほとんどのケースでミーゼス応力が用いられています。
理由の1 つが延性材料における降伏評価への適用性です。実験においては、トレスカ応力説よりもミーゼス応力説がより正確であると示されています。[2]
また、CAEソフトウェアへの実装上の都合も理由と思われます。トレスカの降伏曲面はトレスカ応力を![]() =
=![]() (定数)として主応力空間で図示すると、
(定数)として主応力空間で図示すると、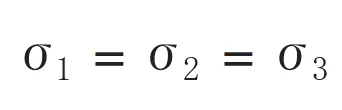 を中心軸とする半径
を中心軸とする半径![]() の円筒に内接する六角柱表面になり、プログラムが複雑になってしまいます。(図14)
の円筒に内接する六角柱表面になり、プログラムが複雑になってしまいます。(図14)
実際、Ansysをはじめ多くの商用CAEソフトウェアでは、弾塑性解析にミーゼスの降伏条件が採用されています。(この場合、解析結果としてトレスカ応力を表示できますが、塑性の判定にはトレスカの降伏条件は利用されていないため注意が必要です)
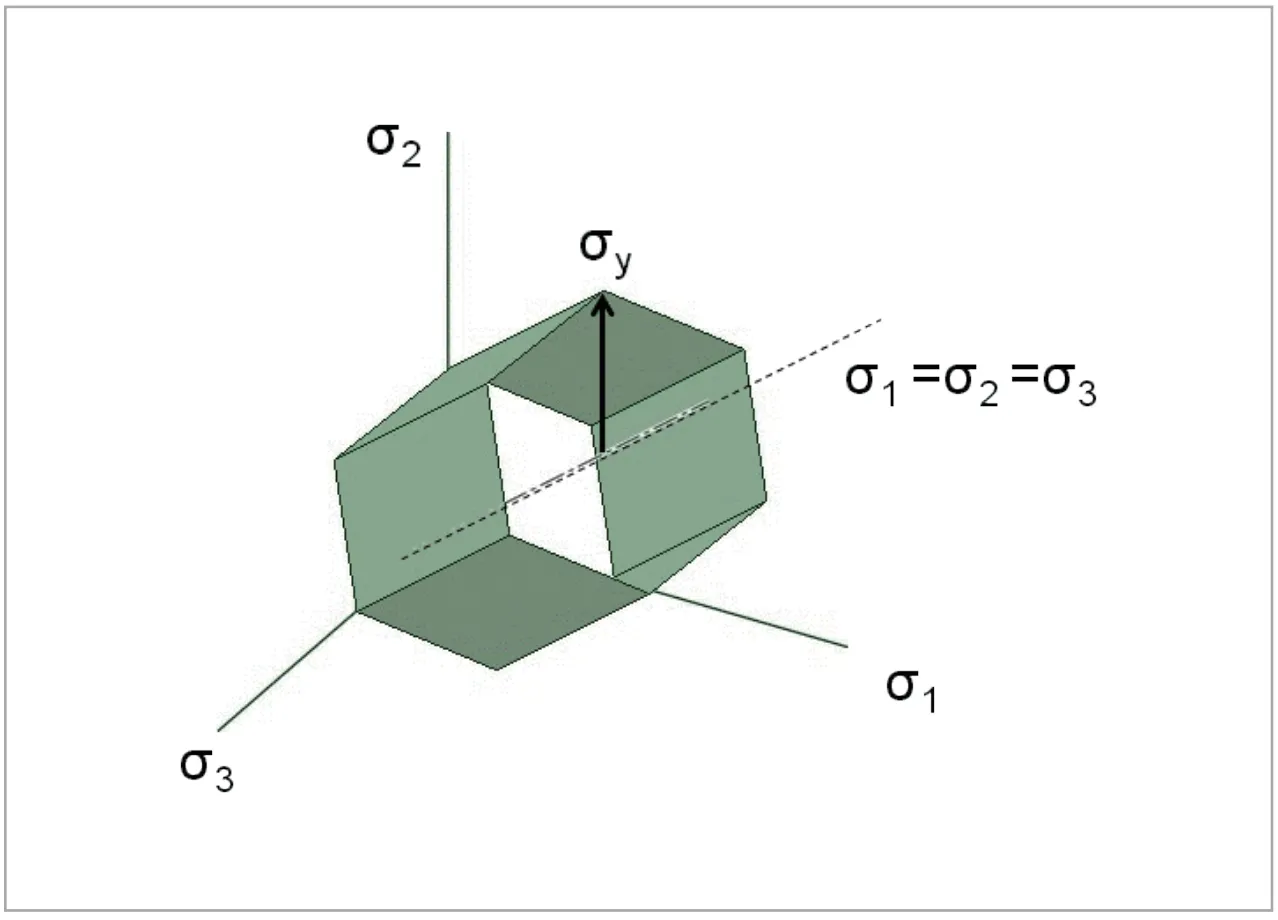
図14 トレスカの降伏曲面
6 まとめ ~ミーゼス応力をどう説明するか?
- ミーゼス応力はせん断ひずみエネルギー説に基づいており、延性材料の降伏予測に適した判定基準である。
- ミーゼス応力値と材料の降伏応力を比較することで、延性材料の塑性の発生有無を判断できる。
- ミーゼス応力はスカラー量であり、引張・圧縮の区別が無い。(適宜、最大主応力や最小主応力を併用する)
- 主応力はせん断成分がゼロのため延性材料の強度評価には適さない。ミーゼス応力は、トレスカ応力(応力強さ)や最大せん断応力よりも正確であることが実験で確かめられており、延性材料の強度評価に適している。
7 おわりに
ミーゼス応力はCAEではもっともポピュラーな解析結果ですが、必ずしもその性質が理解されているとはいえないと思います。もし意味を知らずに利用すれば、設計の方向性を間違えることにもつながってしまいます。
どんなにCAEソフトが簡単になっても、最終的に結果を評価するのは人です。CAE結果を使う以上、結果の意味を正確に伝えることがCAE担当者の責務であると思い、本稿を執筆いたしました。皆様の業務に少しでもお役立ていただけましたら幸いです。
※補足
応力を「大きさと方向を持つ物理量」と考えた場合、ミーゼス応力やトレスカ応力のような方向を持たない値は、厳密には応力よりも「判定式」や「判定指標」と呼ぶ方が適切かと思います。しかし、一般の商用CAEソフトではこれらを全部「応力」として分類していることが多いため、本稿では解りやすさを優先して特に区別せずに応力として記載いたしました。
参考文献
[1] 「例題で学ぶ連続体力学」 非線形CAE協会(編)、石井 建樹・只野裕一・加藤 準治・車谷 麻緒(共著) 森北出版
[2] 日本機械学会論文集 機械学会設計・建設規格事例規格における弾塑性有限要素解析を用いたクラス1器に対する強度評価手法 朝田誠治, 平野隆, 永田徹也, 笠原直人
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

実測 × 解析で基板の熱変形問題を解決!基板反り現象の高精度シミュレーション
~エスペック(株)×サイバネットシステム(株)の連携ソリューション~
-

【全記事】CAEのあるものづくり vol.42
ユーザー様インタビュー記事7件を1冊に集約した保存版
-

誤差との上手なつきあい方 ~流体解析の計算誤差~ (完全保存版)
誤差との上手なつきあい方 前編・後編 を1冊にまとめた保存版 PDF
-

非線形解析の最大強度評価はAnsys LS-DYNAで解決!
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析で電子機器の信頼性向上
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

共振回避だけで終わらせない振動解析の進め方を解説(周波数応答・時刻歴まで)
~Ansys Mechanicalで実現する高度な製品開発~