CAEを学ぶ
粘弾性モデルの基礎(後編)
佐賀大学 大学院工学系研究科 機械システム工学専攻 只野 裕一 様
粘弾性モデルの基礎(後編)の概要
粘弾性モデルの基礎(前編/後編) 完全保存版 PDF を無料公開中
粘弾性モデルの基礎(前編/後編) 完全保存版 PDF サンプル
これさえ読めば粘弾性モデルの基礎がわかる
全2回のシリーズとなっております「粘弾性モデルの基礎」について、前編/後編を1冊でお読みいただける完全保存版 PDF を公開いたしました。どなたでも簡単なフォーム入力のみでダウンロードいただけますので、是非この機会にご利用ください。
【ページ数】13 ページ
【ファイル形式】 PDF
【著者】佐賀大学 大学院工学系研究科 機械システム工学専攻
只野 裕一 様
|
【目次】 2. 線形粘弾性モデルの構成要素 3. 線形粘弾性モデルの定式化 4. MaxwellモデルとVoigtモデルの材料応答
|
5. 時間変化する入力を 与えたときの材料応答 6. 線形粘弾性モデルの一般化 7. 線形粘弾z性モデルの 3次元モデルへの 8. おわりに |
時間変化する入力を与えたときの材料応答
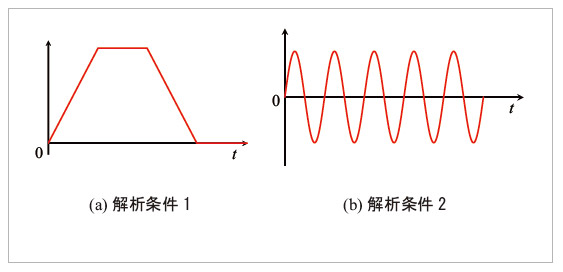
図9 解析条件
5.1 Maxwellモデルの材料応答
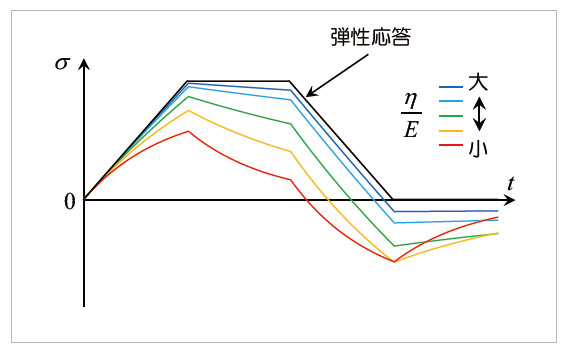
図10 Maxwellモデルによる応力応答(解析条件1)
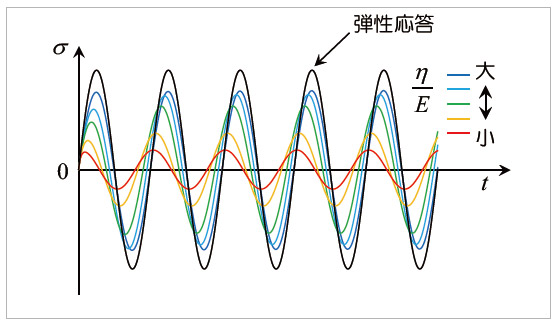
図11 Maxwellモデルによる応力応答(解析条件2)
5.2 Voigtモデルの材料応答
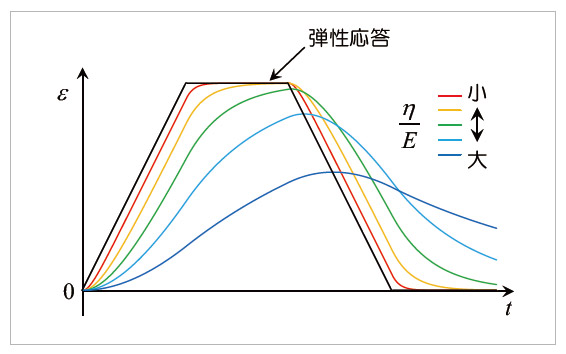
図12 Voigtモデルによるひずみ応答(解析条件1)
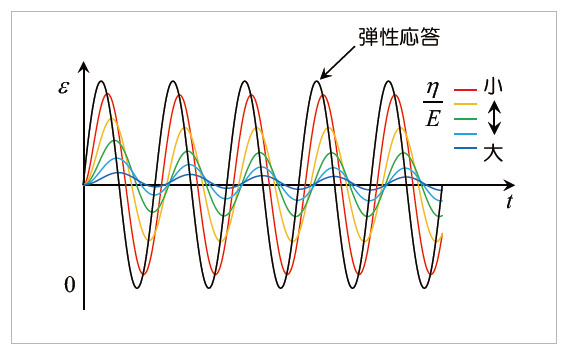
図13 Voigtモデルによるひずみ応答(解析条件2)
線形粘弾性モデルの一般化
6.1 一般化Maxwellモデル
各Maxwell要素が並列に結合されているため、各要素に生じるひずみはモデル全体のひずみεと等しくなります。すなわち、要素数がn個の一般化Maxwellモデルに対して
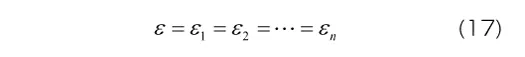
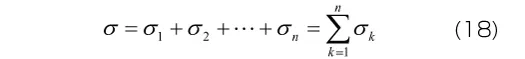
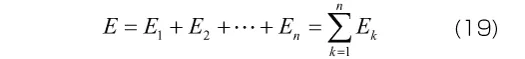
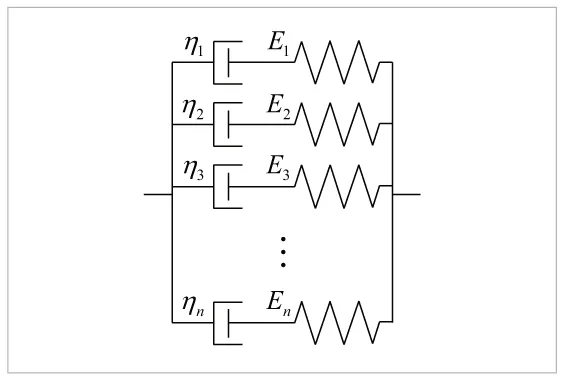
図14 一般化Maxwellモデル
6.2 一般化Voigtモデル
各Voigt要素が直列に結合されていることから、各要素に生じる応力がモデル全体の応力σと等しくなります。すなわち、要素数がn個の一般化Voigtモデルに対して
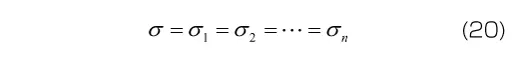
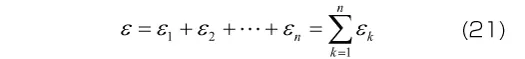
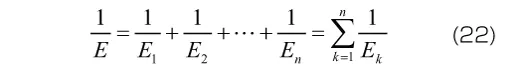
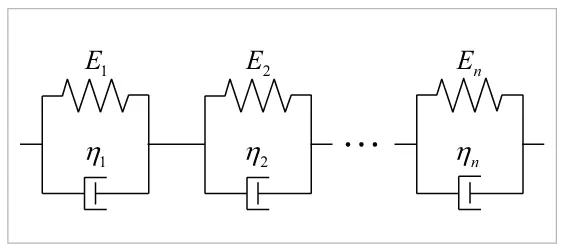
図15 一般化Voigtモデル
6.3 一般化Maxwellモデルと一般化Voigtモデルの材料応答
2要素で構成される一般化Maxwellモデルにひずみ入力を与えた際の、応力応答を図16に示します。要素1は弾性係数、粘性係数がともに要素2よりも大きい要素としています。2つのMaxwell要素がそれぞれ単体で存在するときの材料応答がそれぞれ青と赤の破線であり、全体の材料応答(緑の実線)はその和となっています。要素1の応力が全体的に要素2よりも高くなっていますが、これは要素1の弾性係数が要素2の弾性係数より大きいためです。すなわち、モデル全体の材料応答に各要素がどの程度寄与するかは、各要素の弾性係数の大きさによって決まることになります。要素数を増やした場合にも、全体の材料応答は常に各要素の応答の総和として与えられます。これにより、単体のMaxwellモデルでは表現できなかった複雑な材料応答を表現することが可能となります。
図17は、2要素で構成される一般化Voigtモデルに応力入力を与えた際のひずみ応答です。ここでは、要素1は弾性係数、粘性係数がともに要素2よりも小さい要素としています。一般化Maxwellモデルと同様、全体の材料応答は要素1と要素2の応答の和となっていることがわかります。また、各要素が全体の材料応答にどの程度寄与するかは、各要素の弾性コンプライアンスの大きさで決まります。要素数が増加した場合でも、各要素の材料応答の総和が全体の応答として得られ、これにより単体のVoigtモデルでは表現できない複雑な応答を表すことができます。
一般化Maxwellモデルや一般化Voigtモデルは、要素の数が増えるほど材料定数の数も増加するため、より複雑な材料挙動を表現しようとすると材料定数の同定が難しくなる傾向があります。手作業での材料定数同定には限界があるため、最適化手法を導入し、いくつかの材料試験の結果から数値的にパラメータを決定することがしばしば行われます。また最近の汎用CAEソフトウェアでは、最適化手法による材料定数の自動同定を標準機能として備えている場合もありますので、そのような機能を利用することで効率的な材料定数の決定を行うことができます。
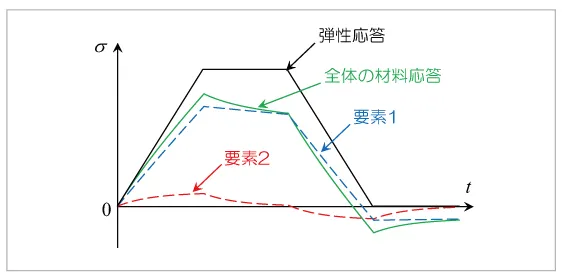
図16 一般化Maxwellモデルによる応力応答
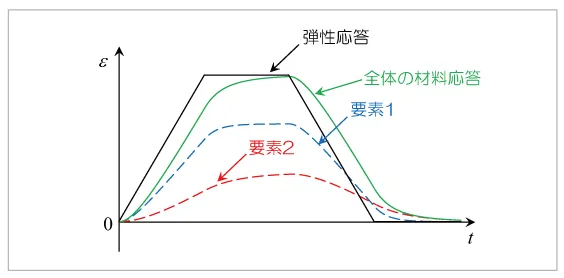
図17 一般化Voigtモデルによるひずみ応答
線形粘弾性モデルの3次元モデルへの拡張
ここまでに示した線形粘弾性モデルは、いずれも1次元的な応力・ひずみ応答に限定して解説してきました。モデルの性質を理解する上で1次元モデルは非常に有効ですが、現実的な変形解析のほとんどは2次元もしくは3次元問題となるため、実用的な材料モデルとしては1次元モデルを3次元モデルへと拡張することが必要になります。そこで本節では、線形粘弾性モデルの3次元モデルへの拡張について考えてみましょう。なお本稿では最も簡単な拡張として、等方粘弾性モデルに限って説明します。また、以下ではMaxwellモデルおよびVoigtモデルについて示しますが、一般化Maxwellモデルや一般化Voigtモデルでも考え方は全く同じです。
線形粘弾性モデルを3次元へ拡張する場合、一般に応力とひずみを体積成分と偏差成分に分離し、それぞれに対して1次元の場合と同様のモデルを仮定します。これは、弾塑性モデルを1次元から3次元へと拡張するときと同じ考え方です。応力の体積成分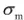 と偏差成分
と偏差成分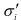 は、それぞれ次式で定義されます。
は、それぞれ次式で定義されます。
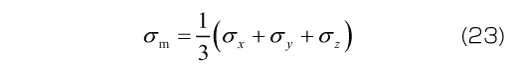
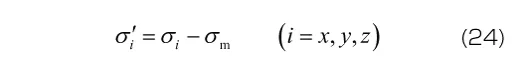
応力の体積成分は、静水圧もしくは平均応力と呼ばれます。また偏差成分を偏差応力と呼び、x , y , z 方向の各垂直応力からそれぞれ平均応力を引いたものとなります。なお偏差応力のせん断成分については、もとの応力のせん断成分と同じとなります(すなわち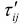 =
=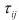 ( i , j = x , y , z ) )。同様にして、ひずみの体積成分
( i , j = x , y , z ) )。同様にして、ひずみの体積成分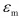 と偏差成分
と偏差成分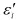 も定義できます。
も定義できます。
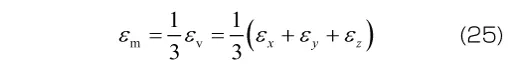
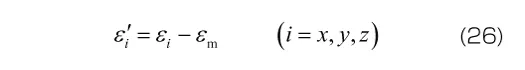
ひずみの体積成分は平均ひずみであり、体積ひずみの1/3となります。また応力と同様に、偏差ひずみのせん断成分はもとのひずみのせん断成分と等しくなります(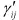 =
=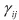 ( i , j = x , y , z )。以上を用いて、MaxwellモデルとVoigtモデルを3次元モデルに拡張してみましょう。
( i , j = x , y , z )。以上を用いて、MaxwellモデルとVoigtモデルを3次元モデルに拡張してみましょう。
7.1 Maxwellモデルの3次元モデルへの拡張
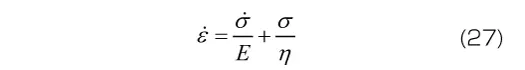

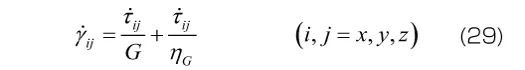
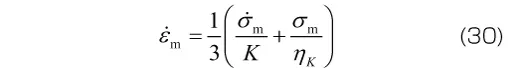
G , K はせん断弾性係数と体積弾性係数であり、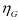 ,
,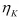 はせん断粘性係数、体積粘性係数と呼ばれます。材料定数が体積変形とせん断変形のそれぞれに必要となるため、材料定数の数は2倍になります。なお、体積変形には粘性の効果はほとんど現れないと考え、体積変形に対する変形を表す式(30)の右辺括弧内の第2項を無視する(すなわち体積粘性係数
はせん断粘性係数、体積粘性係数と呼ばれます。材料定数が体積変形とせん断変形のそれぞれに必要となるため、材料定数の数は2倍になります。なお、体積変形には粘性の効果はほとんど現れないと考え、体積変形に対する変形を表す式(30)の右辺括弧内の第2項を無視する(すなわち体積粘性係数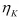 が十分に大きく、弾性応答が得られると考える)こともあります。この場合、材料定数の数は1次元モデルと同じになります。
が十分に大きく、弾性応答が得られると考える)こともあります。この場合、材料定数の数は1次元モデルと同じになります。
7.2 Voigtモデルの3次元モデルへの拡張
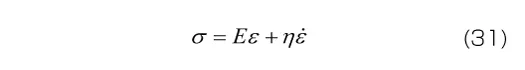
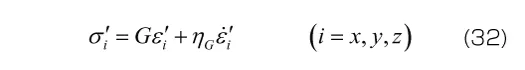
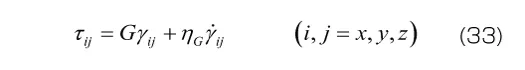
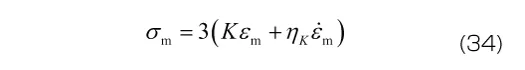
ここでも材料定数が体積変形とせん断変形のそれぞれに必要となるため、材料定数の数は2倍になります。また、体積変形には粘性の効果が無視できると考える場合には、式(34)の右辺括弧内の第2項を無視します(体積粘性係数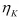 を0とすることで、弾性応答に帰着させる)。この場合、材料定数の数は1次元モデルと同じになります。
を0とすることで、弾性応答に帰着させる)。この場合、材料定数の数は1次元モデルと同じになります。
おわりに
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

実測 × 解析で基板の熱変形問題を解決!基板反り現象の高精度シミュレーション
~エスペック(株)×サイバネットシステム(株)の連携ソリューション~
-

【全記事】CAEのあるものづくり vol.42
ユーザー様インタビュー記事7件を1冊に集約した保存版
-

誤差との上手なつきあい方 ~流体解析の計算誤差~ (完全保存版)
誤差との上手なつきあい方 前編・後編 を1冊にまとめた保存版 PDF
-

非線形解析の最大強度評価はAnsys LS-DYNAで解決!
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析で電子機器の信頼性向上
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

共振回避だけで終わらせない振動解析の進め方を解説(周波数応答・時刻歴まで)
~Ansys Mechanicalで実現する高度な製品開発~