CAEを学ぶ
粘弾性モデルの基礎(前編)
佐賀大学 大学院工学系研究科 機械システム工学専攻 只野 裕一 様
粘弾性モデルの基礎(前編)の概要
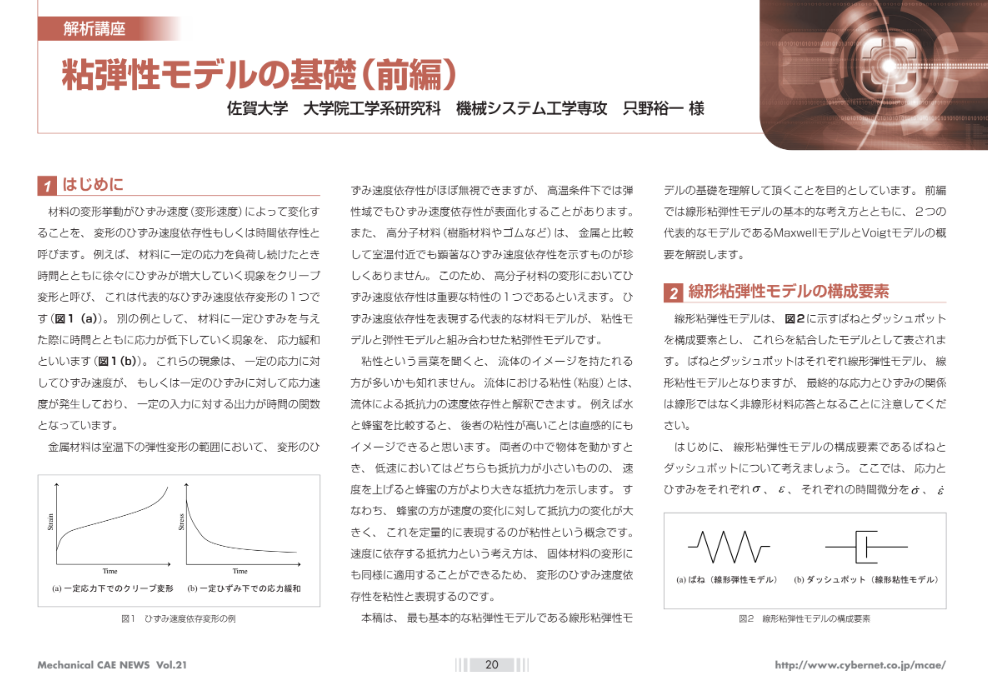
粘弾性モデルの基礎(前編/後編) 完全保存版 PDF を無料公開中
粘弾性モデルの基礎(前編/後編) 完全保存版 PDF サンプル
これさえ読めば粘弾性モデルの基礎がわかる
全2回のシリーズとなっております「粘弾性モデルの基礎」について、前編/後編を1冊でお読みいただける完全保存版 PDF を公開いたしました。どなたでも簡単なフォーム入力のみでダウンロードいただけますので、是非この機会にご利用ください。
【ページ数】13 ページ
【ファイル形式】 PDF
【著者】佐賀大学 大学院工学系研究科 機械システム工学専攻
只野 裕一 様
|
【目次】 2. 線形粘弾性モデルの構成要素 3. 線形粘弾性モデルの定式化 4. MaxwellモデルとVoigtモデルの材料応答
|
5. 時間変化する入力を 与えたときの材料応答 6. 線形粘弾性モデルの一般化 7. 線形粘弾z性モデルの 3次元モデルへの 8. おわりに |
はじめに
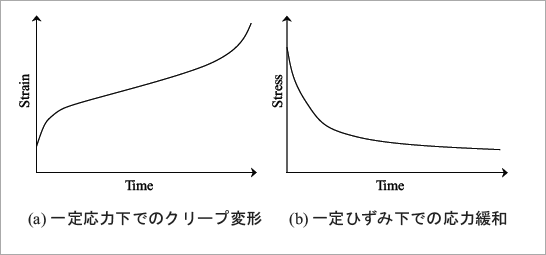
図1 ひずみ速度依存変形の例
粘性という言葉を聞くと、 流体のイメージを持たれる方が多いかも知れません。 流体における粘性(粘度)とは、流体による抵抗力の速度依存性と解釈できます。 例えば水と蜂蜜を比較すると、 後者の粘性が高いことは直感的にもイメージできると思います。 両者の中で物体を動かすとき、 低速においてはどちらも抵抗力が小さいものの、 速度を上げると蜂蜜の方がより大きな抵抗力を示します。 すなわち、 蜂蜜の方が速度の変化に対して抵抗力の変化が大きく、 これを定量的に表現するのが粘性という概念です。速度に依存する抵抗力という考え方は、 固体材料の変形にも同様に適用することができるため、 変形のひずみ速度依存性を粘性と表現するのです。
本稿は、 最も基本的な粘弾性モデルである線形粘弾性モデルの基礎を理解して頂くことを目的としています。 前編では線形粘弾性モデルの基本的な考え方とともに、 2つの代表的なモデルであるMaxwellモデルとVoigtモデルの概要を解説します。
線形粘弾性モデルの構成要素
線形粘弾性モデルは、 図2に示すばねとダッシュポットを構成要素とし、 これらを結合したモデルとして表されます。 ばねとダッシュポットはそれぞれ線形弾性モデル、 線形粘性モデルとなりますが、 最終的な応力とひずみの関係は線形ではなく非線形材料応答となることに注意してください。
はじめに、 線形粘弾性モデルの構成要素であるばねとダッシュポットについて考えましょう。 ここでは、 応力とひずみをそれぞれσ 、 ε 、 それぞれの時間微分を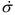 、
、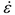 とします。 簡単のために1次元問題で考え、 微小変形を想定しています。 3次元モデルへの拡張については、 後編で解説します。
とします。 簡単のために1次元問題で考え、 微小変形を想定しています。 3次元モデルへの拡張については、 後編で解説します。
ばね(線形弾性モデル)は応力とひずみが比例するというモデルで、 いわゆる線形弾性変形を表現します。 すなわち、 応力とひずみの間につぎの関係を仮定します。
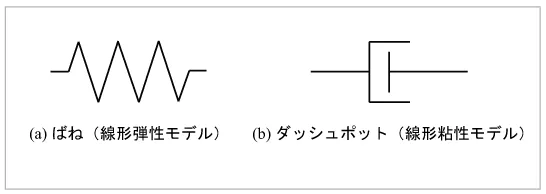
図2 線形粘弾性モデルの構成要素
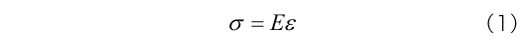
ばねの変形は速度に依存しない、すなわち入力に対して瞬時に変形するモデルであり、これは固体的な変形特性と捉えることができます。ばねの変形の特徴として、応力とひずみが常に1対1に対応することが挙げられます。
つぎにダッシュポット(線形粘性モデル)は、応力とひずみ速度が比例するというモデルです。
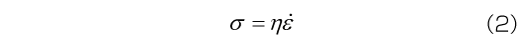
線形粘弾性モデルの定式化
3.1 Maxwellモデル
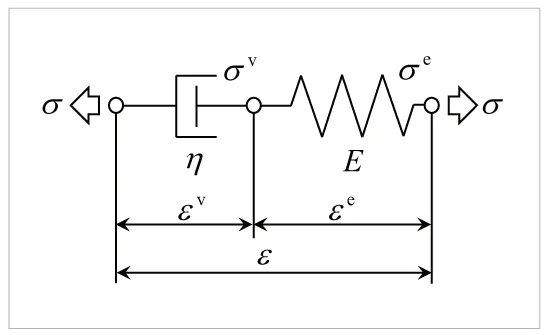
図3 Maxwellモデル
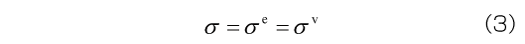
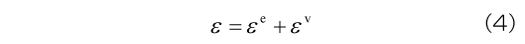
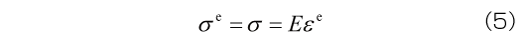

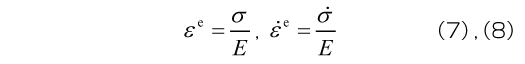
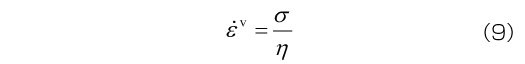
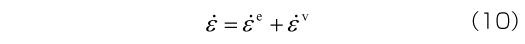
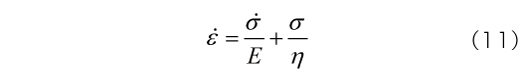
3.2 Voigtモデル
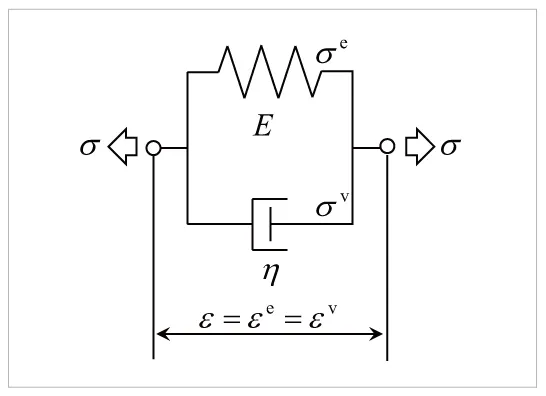
図4 Voigtモデル
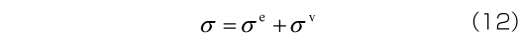
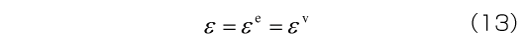
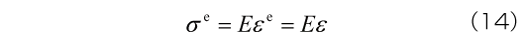
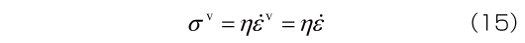
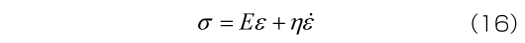
MaxwellモデルとVoigtモデルの 材料応答
4.1 Maxwellモデルの材料応答
まず、Maxwellモデルに一定応力(図5(a))を入力として与えた場合を考えてみましょう。はじめは応力が0 であり、 ある時刻(図中では時刻t = 0)で瞬間的に一定応力σを入力します。 応力が一定なので、 時刻t = 0 を除いて常に応力速度は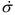 = 0 となります。 このとき得られるひずみの時刻歴を、 図6に示します。 時刻t = 0 で
= 0 となります。 このとき得られるひずみの時刻歴を、 図6に示します。 時刻t = 0 で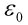 =
=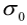 /Eが瞬間的に生じています。これは弾性変形によるひずみとなり、この性質を瞬間弾性と呼びます。その後、時間とともに一定のひずみ速度でひずみが増加します。すなわち、一定応力に対して無制限にひずみが発生することがわかります。時刻t におけるひずみはつぎで与えられます。
/Eが瞬間的に生じています。これは弾性変形によるひずみとなり、この性質を瞬間弾性と呼びます。その後、時間とともに一定のひずみ速度でひずみが増加します。すなわち、一定応力に対して無制限にひずみが発生することがわかります。時刻t におけるひずみはつぎで与えられます。
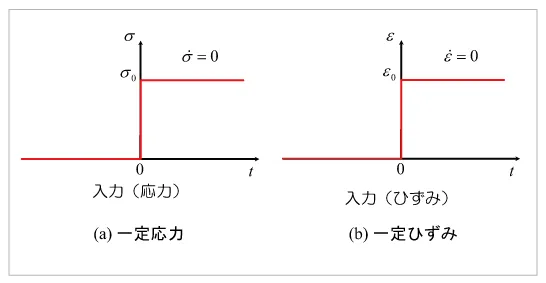
図5 一定応力と一定ひずみ
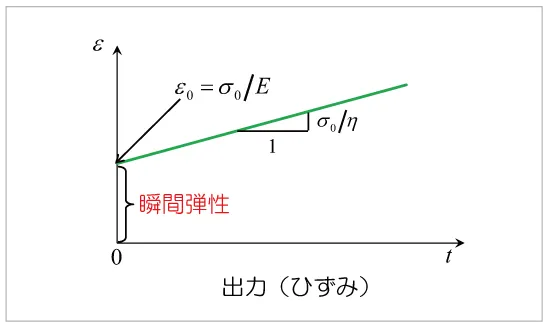
図6 一定応力下でのMaxwellモデルのひずみ応答
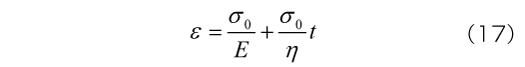
瞬間弾性が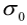 /E 、ひずみ速度(ひずみ応答の傾き)が
/E 、ひずみ速度(ひずみ応答の傾き)が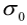 /η で与えられることから、弾性係数E が大きいほど瞬間弾性は小さくなり、また粘性係数η が大きいほどひずみ速度が小さくなることがわかります。もう1 つの例として、図5(b)に示す一定ひずみを入力としたときの応答を考えます。はじめはひずみが0 であり、 ある時刻(図中では時刻t = 0)で瞬間的に一定ひずみε を入力します。 すなわち、 時刻t = 0 を除いてひずみ速度が
/η で与えられることから、弾性係数E が大きいほど瞬間弾性は小さくなり、また粘性係数η が大きいほどひずみ速度が小さくなることがわかります。もう1 つの例として、図5(b)に示す一定ひずみを入力としたときの応答を考えます。はじめはひずみが0 であり、 ある時刻(図中では時刻t = 0)で瞬間的に一定ひずみε を入力します。 すなわち、 時刻t = 0 を除いてひずみ速度が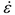 = 0となります。 このとき得られる応力の時刻歴が図7です。 時刻t = 0で弾性変形による応力
= 0となります。 このとき得られる応力の時刻歴が図7です。 時刻t = 0で弾性変形による応力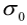 =
= 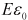 が瞬間的に生じた後、応力が徐々に減少して0に漸近しており、一定ひずみ下での応力緩和が表現されています。時刻t における応力はつぎで与えられます。
が瞬間的に生じた後、応力が徐々に減少して0に漸近しており、一定ひずみ下での応力緩和が表現されています。時刻t における応力はつぎで与えられます。
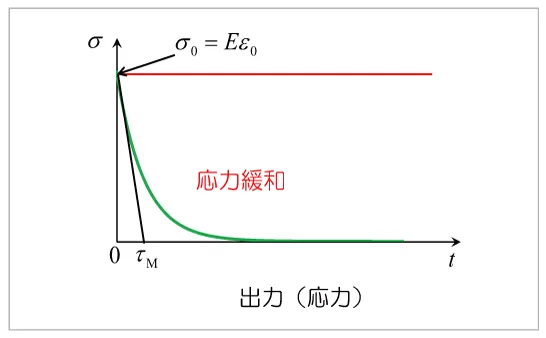
図7 一定ひずみ下でのMaxwellモデルの応力応答
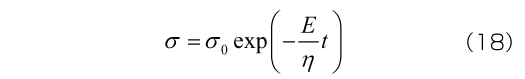
ここで 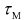 = η / E を緩和時間と呼びます。緩和時間は、図7に示すように時刻t = 0におけるひずみ応答の接線と時間軸との交点を表しており、緩和時間が短いほど応力が短時間で緩和することを意味しています。弾性係数が大きくなるほど、また粘性係数が小さくなるほど、緩和時間は短くなります。以上に示したように、Maxwellモデルに応力やひずみを入力すると、ばねによる弾性応答が瞬間的に発生し、その後ダッシュポットによる粘性応答が時間とともに進行します。
= η / E を緩和時間と呼びます。緩和時間は、図7に示すように時刻t = 0におけるひずみ応答の接線と時間軸との交点を表しており、緩和時間が短いほど応力が短時間で緩和することを意味しています。弾性係数が大きくなるほど、また粘性係数が小さくなるほど、緩和時間は短くなります。以上に示したように、Maxwellモデルに応力やひずみを入力すると、ばねによる弾性応答が瞬間的に発生し、その後ダッシュポットによる粘性応答が時間とともに進行します。
4.2 Voigtモデルの材料応答
つぎに、Voigtモデルに図5(a)の一定応力を入力した場合を考えましょう。図8 にひずみの時刻歴を示します。時刻t = 0では0であったひずみが時間とともに増加していき、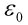 =
= 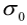 / Eに漸近していきます。 ここで
/ Eに漸近していきます。 ここで 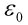 =
= 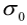 / Eは弾性モデルにおいて生じるひずみとなっています。弾性応答に漸近していくこの性質を遅延弾性と呼びます。このとき、時刻t におけるひずみはつぎで与えられます。
/ Eは弾性モデルにおいて生じるひずみとなっています。弾性応答に漸近していくこの性質を遅延弾性と呼びます。このとき、時刻t におけるひずみはつぎで与えられます。
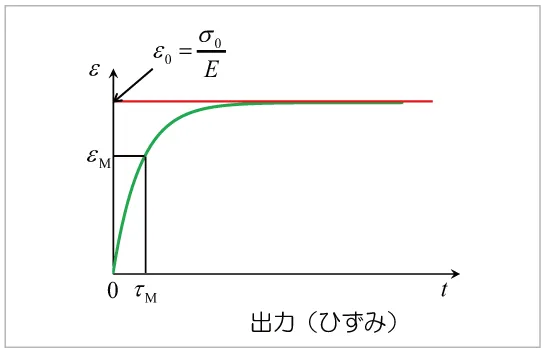
図8 一定応力下でのVoigtモデルのひずみ応答
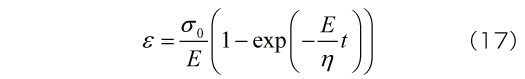
ここで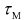 = η / E を遅延時間と呼びます。遅延時間は、ひずみが
= η / E を遅延時間と呼びます。遅延時間は、ひずみが 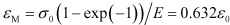 となるのに要する時間を表しており、遅延時間が大きいほど弾性応答への収束に時間を要することを表しています。Maxwellモデルの緩和時間と定義式は同じですが、物理的な意味は異なるので注意してください。弾性係数が大きくなるほど、また粘性係数が小さくなるほど、遅延時間は短くなります。
となるのに要する時間を表しており、遅延時間が大きいほど弾性応答への収束に時間を要することを表しています。Maxwellモデルの緩和時間と定義式は同じですが、物理的な意味は異なるので注意してください。弾性係数が大きくなるほど、また粘性係数が小さくなるほど、遅延時間は短くなります。
このように、Voigtモデルは入力に対して弾性応答が直ちには発生せず、時間の経過とともに弾性応答へ漸近するという材料挙動を表現します。
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

実測 × 解析で基板の熱変形問題を解決!基板反り現象の高精度シミュレーション
~エスペック(株)×サイバネットシステム(株)の連携ソリューション~
-

【全記事】CAEのあるものづくり vol.42
ユーザー様インタビュー記事7件を1冊に集約した保存版
-

誤差との上手なつきあい方 ~流体解析の計算誤差~ (完全保存版)
誤差との上手なつきあい方 前編・後編 を1冊にまとめた保存版 PDF
-

非線形解析の最大強度評価はAnsys LS-DYNAで解決!
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析で電子機器の信頼性向上
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

共振回避だけで終わらせない振動解析の進め方を解説(周波数応答・時刻歴まで)
~Ansys Mechanicalで実現する高度な製品開発~