はじめてみよう！流体解析（実践編）〜誤差との上手なつき合い方(1)〜

はじめに

現在、製品開発の現場において、CAEが使用されることは一般的になり、設計から試作、検証、量産まで様々な工程で解析の必要性が高まっています。

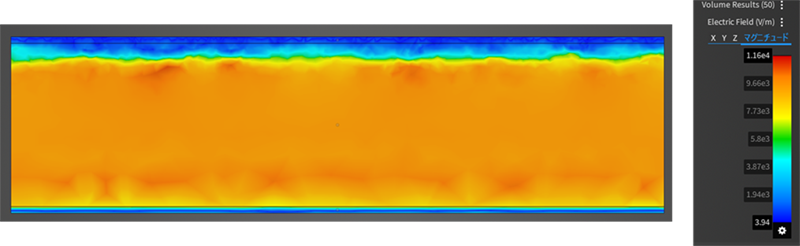
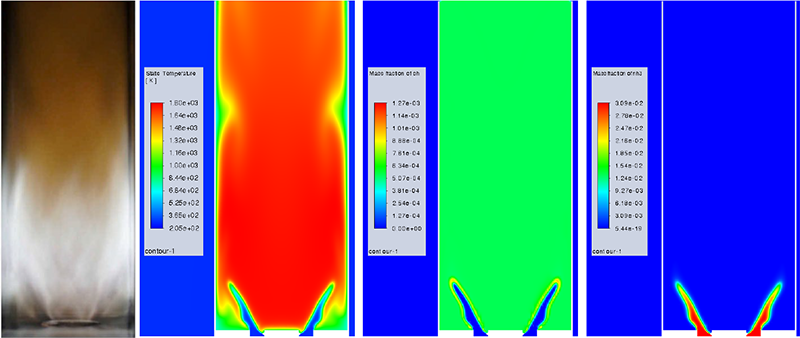
一例を挙げますと、発熱素子を含む筐体では、熱逃げ経路としては熱伝導だけではなく熱伝達の影響度合いも大きいため、精度良く解析するには熱伝達による熱移動を正確に解析する必要があります。このため、伝熱による解析ではなく周囲の流体挙動も解くことが可能な熱流体解析が必要となります。

例えば、「CAEソフトの使い方はある程度習熟したが、実験結果と解析結果に差があり、実験が再現できない」とお悩みの方は多いのではないでしょうか？この連載では、そうした「誤差」と上手につきあう方法について、具体例をもとに解説していきます。さらに解析を有効活用するための一助となれば幸いです。

避けられない実現象との「誤差」

実験でも解析でも、実現象を空間的・時間的にすべて再現できるわけではなく、なんらかの仮定のもとに実現象の一部分を再現しているにすぎません。そのため、実験、解析とも結果に誤差（実現象との差）を含みますので、実験と解析の間にも差（＝ギャップ）が必ず発生します（図１）。

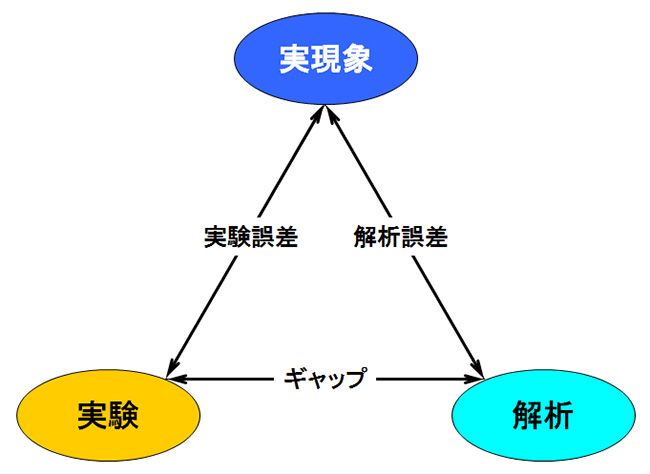
図１　実現象-実験-解析の誤差とギャップ

しかし、誤差があるから解析結果が使えないわけではありません。目的によっては、そのままで必要十分な知見が得られることもあるでしょう。また、実験や解析で生じる誤差には原因があります。この原因を理解して、それぞれの誤差を減らし、実験と解析のギャップを減らすことができれば、実験も解析もより有効に活用できるようになります。

「誤差」とのつきあい方は目的次第 ～定性評価と定量評価～

繰り返しになりますが、実験も解析も実現象の一部を再現しているに過ぎません。そこで効率よく実験、解析を行うには、【何を知りたいか】と【かけられるコスト】をはっきりさせておくことが重要です。知りたい対象が明確であればあるほど、実現象と近づけることが容易になります。

これは実験結果と解析結果をすりあわせる際も同様です。特に、【その目的が定性評価なのか、それとも定量評価なのか？】を意識すると分かりやすいでしょう。
「定性評価」は対象物の傾向を把握することを指し、例えば「ポンプを駆動した場合にどの箇所で圧力が低くなるか」を知りたい場合は定性評価となります。これに対して、「定量評価」は対象物を数値で把握することです。例えば「ポンプを駆動した場合に最も低くなる箇所の圧力値」を知りたい場合は定量評価となります。

定量評価の方がそれぞれの誤差を減らし、ギャップを減らす必要がありますので、時間、費用などの計算コストが高くなります。
もし傾向だけ見たいなら定性評価だけで十分ですが、数値データもきちんとすり合せたい場合は定量評価が必要です。しかし、いきなり定量評価に取り組むのは計算コストがかるので、まずは第一段階として定性的な比較を行うことをお勧めします。定性的な結果が合致するようになれば、例えば実験ができない条件での傾向を知るために解析を活用できるようになります。第二段階として定量的な比較を行います。定量的な結果が合致するようになれば、例えば実験で条件を変化させた場合の結果予測に解析を使うことができ、実験回数の低減に繋がります。

「誤差」を減らすために ～発生要因とその対策～

目的が明確になったら、具体的に誤差を減らしていく方法を考えましょう。
本連載では、実験と解析のそれぞれで誤差が生じる理由とその対処法を解説していきます。
初回である今回は、実験、解析それぞれの誤差要因を紹介します。次号以降では、工程ごとに二つの解析モデルを使用し、モデル化の違いが結果（誤差）に及ぼす影響について述べ、解析を有効活用するために考慮すべき点をご説明します。

実験誤差

実験誤差は実験を行った際に生じる誤差で、例えば以下が挙げられます。

1. 測定器の校正状態や実験装置の設定状態など測定器や実験装置に起因する誤差
2. 測定値の読み取りに対する個人差など人為的な誤差
3. その他雰囲気温度による誤差など制御できない要因による誤差

これらの誤差は測定器・実験装置の状態を良好に保ち、実験の回数を増やすなどの工夫によって減らすことはできます。しかしゼロにすることはできないため、「そもそも実験結果には誤差が含まれる」ことを認識しておく必要があります。

解析誤差

解析誤差は解析を行った際に生じる誤差で、解析工程順に以下の５つに分けることができます。

1. モデル形状による誤差
   形状簡略化や解析領域サイズ、モデル対称性によって生じる誤差
2. メッシュによる誤差
   メッシュサイズ、メッシュ品質によって生じる誤差
3. モデル化による誤差
   乱流モデルの選択、物性値、圧縮性（非圧縮性）、境界条件などによって生じる誤差
4. 計算誤差
   丸め誤差や打ち切り誤差など数値解析で生じる誤差
5. 結果処理による誤差
   結果処理の方法が適当でないこと（実験と比較している物理量が異なるなど）によって生じる誤差

実際に解析を行った際に生じる誤差はこれらが複合的に組み合わさっていますが、それぞれの誤差の原因を理解し、どの誤差が主要因になるかを見極めて対処することで、それらを小さくすることが可能です。

おわりに

いかがでしたか？第２回では、モデル形状によって生じる解析誤差について、事例をもとにご紹介します。どうぞご期待ください。