陽解法(ようかいほう)

陽解法とは、各時間点の応答を求める時刻歴応答解析の一種で、現在の状態（時刻：t）についての運動方程式を直接的に（陽的）解く手法です。
収束計算を必要としないため、非線形性の強い動的問題でも安定して解を得ることができます。
一般に、短時間で大変形するものや、破壊・剥離をともなう問題で利用されます。

陽解法の時間積分法の1つである中央差分法について説明します。
ここで、変位は時間増分Δtにおいて線形と仮定します。

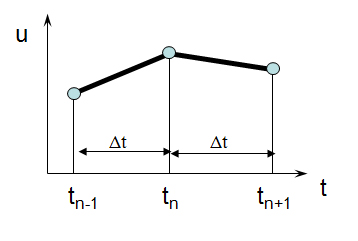
時刻t _n における運動方程式は次のようになります。

時刻t _n における速度および加速度は次のようになります。

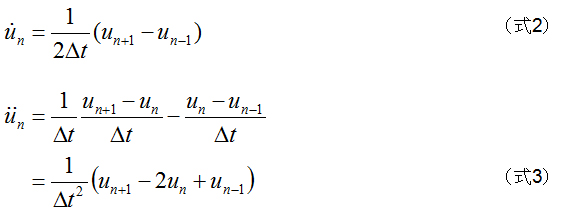
（式2）および（式3）を（式1）に代入します。

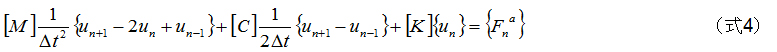
u _n+1 について整理します。

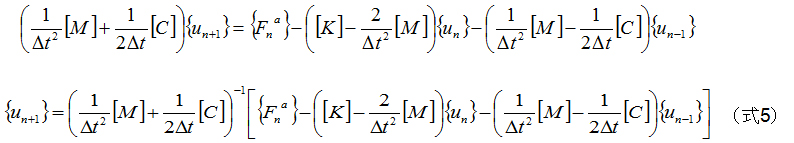
（式5）を良く見てみると、右辺には未知な値{u _n+1 }が存在しないことがわかります。そのため、未知変数{u _n+1 }を既知の値（右辺）で直接的に計算できます。このような計算を陽的であるといいます。
陽的であるため、陰解法の非線形解析で用いるニュートンラプソン法のような反復計算や収束チェックが不要となります。
また、[K]について逆行列が必要ありません。[M] ^-1 および[C] ^-1 の項がありますが、[M]と[C]を対角化しておけば逆行列を求める必要がなくなります。（対角化した[M]を集中質量マトリクスと呼びます）

逆行列を求めるには多くの計算コストを要しますが、逆行列が必要なくなることで、陽解法では1回あたりの計算コストが、陰解法よりも劇的に小さくなります。

その反面、時間増分Δtがクリティカル時間ステップサイズ（Δt ^crit ）よりも大きくとると、解が不安定となり発散に至る場合があります。
解の安定限界を保証するために、十分に小さな時間ステップが必要とされます。
詳しくは「クーラン条件」の項目をご覧ください。

Ansysにおける取扱い

• Ansysでは陽解法動解析用のモジュールをご用意しています。

CAE用語辞典の転載・複製・引用・リンクなどについては、「著作権についてのお願い」をご確認ください。