CAEを学ぶ
等方硬化則(とうほうこうかそく)
英訳:isotropic hardening rule
等方硬化則とは、降伏曲面が初期の相似系を保ちながら、硬化と共に膨張する硬化則です。
等方硬化則は、単調荷重および弾性除荷のもとで材料の挙動をモデル化でき、大ひずみ問題(金属成形問題など)に適しています。
塑性状態からの荷重の反転後に塑性変形を発生するような条件では、良い結果にならない場合があります。
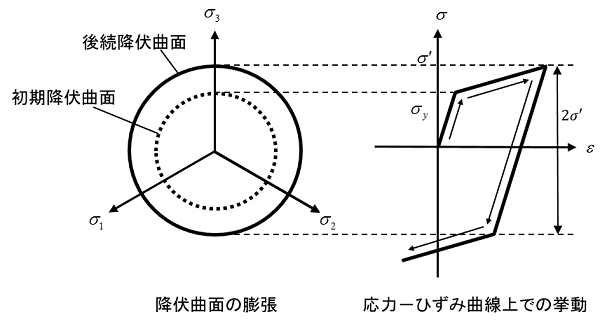
引張と圧縮のサイクル負荷を受ける材料の応力-ひずみ挙動は、下図のように示されます。
等方硬化則では、圧縮時の降伏応力は、引張時に達した最大応力に等しくなります。どの方向においても後続の降伏応力は、荷重履歴の任意の段階で達した最大相当応力に等しくなります。
Ansysにおける取扱い
- Ansysでは移動硬化則、等方硬化則、非線形移動硬化則(Chaboche モデル)などの各種硬化則を取り扱えます。
CAE用語辞典の転載・複製・引用・リンクなどについては、「著作権についてのお願い」をご確認ください。
関連キーワード
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-
剥離・接合強度評価ソリューション ~Ansys Workbench Mechanicalで実施できる剥離解析~
-

レーザー集光の高温レンズ歪みを克服するAnsys連携ソリューション
-
周波数応答解析×自動抽出で干渉チェックを高速化
-

直観的な操作で無線/デジタルフィルタの設計・最適化を支援する〜Ansys Nuhertz FilterSolutions〜
-
流体機器設計の新たな一歩
~Ansys Discoveryで加速する設計改革~
-
筐体の冷却性能を構想設計から見える化 (手戻りを削減できる)
~Ansys Discoveryで始める電気筐体製品の設計改革~
-
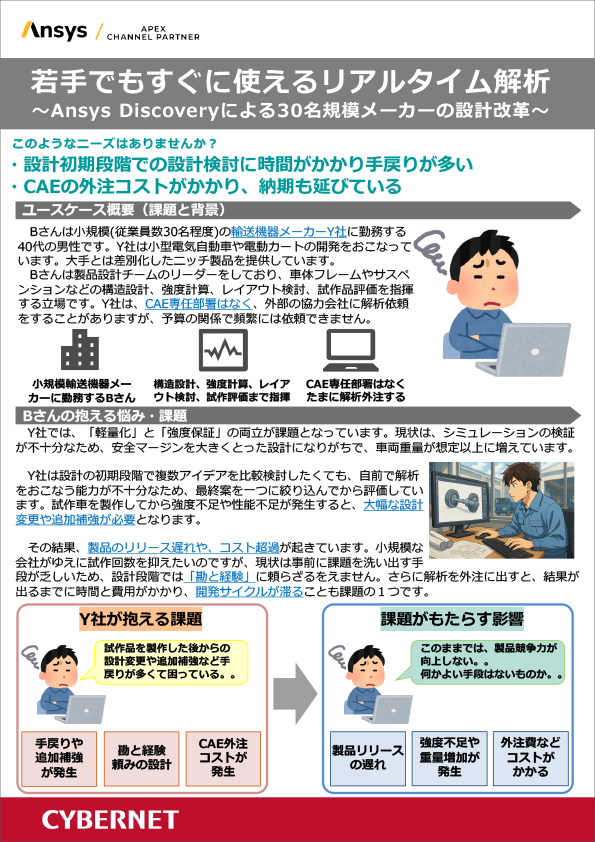
若手でもすぐに使えるリアルタイム解析 (勘と経験からの脱却)
~Ansys Discoveryによる30名規模メーカーの設計改革~
-
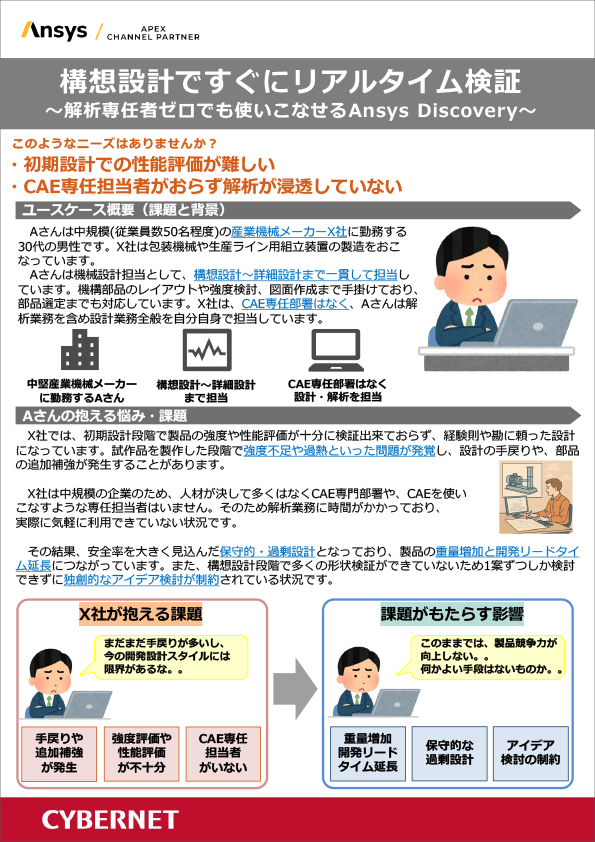
構想設計ですぐにリアルタイム検証 ~解析専任者ゼロでも使いこなせるAnsys Discovery~
~解析専任者ゼロでも使いこなせるAnsys Discovery~