CAEを学ぶ
特異点(とくいてん)
英訳:singularity
有限要素法(FEM)における特異点とは、局所的に高い結果値が出る現象のことで、主に構造解析において問題になります。
構造解析では、角部や拘束端部などに局所的に高い応力が発生する現象として表れます。以下、構造解析を前提として説明します。
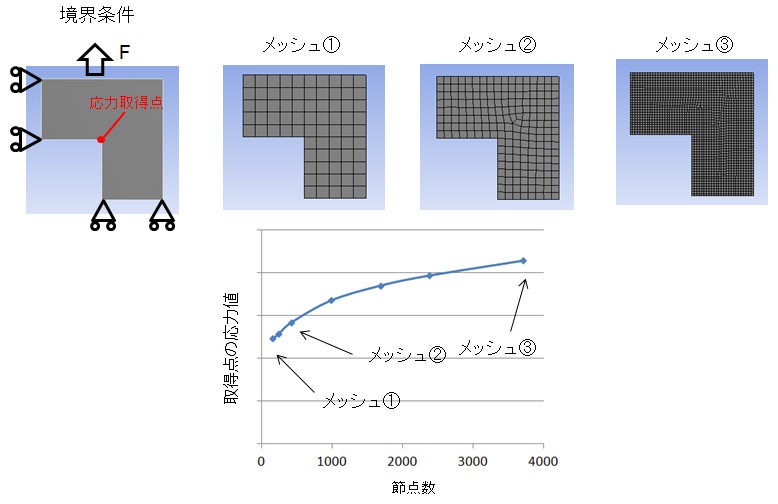
特異点の特徴として、メッシュを細かくしても結果が収束しないことが挙げられます。
一般に、メッシュを細かくすれば次第に応力値が収束していきます。
しかし特異点では、メッシュを細かくすればするほど応力値が上がり、発散していきます。
アダプティブメッシュ(応力値等が収束するまで自動的にメッシュを改善する手法)を利用したときは、収束せずに失敗することがあります。
特異点の応力値は、理論上は無限大となり、評価対象にはできません。
対策として、以下のような方法がよく採られます。
- 特異点近傍の応力は無視して、少し離れた位置で結果を評価する。
- 角部に特異点があり、特異点近傍の応力が重要である場合は、角部に小さなRをつける。(ただしRを表現できるだけの十分なメッシュ分割が必要であり、計算コストはかさむ)
CAE用語辞典の転載・複製・引用・リンクなどについては、「著作権についてのお願い」をご確認ください。
関連キーワード
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-
剥離・接合強度評価ソリューション ~Ansys Workbench Mechanicalで実施できる剥離解析~
-

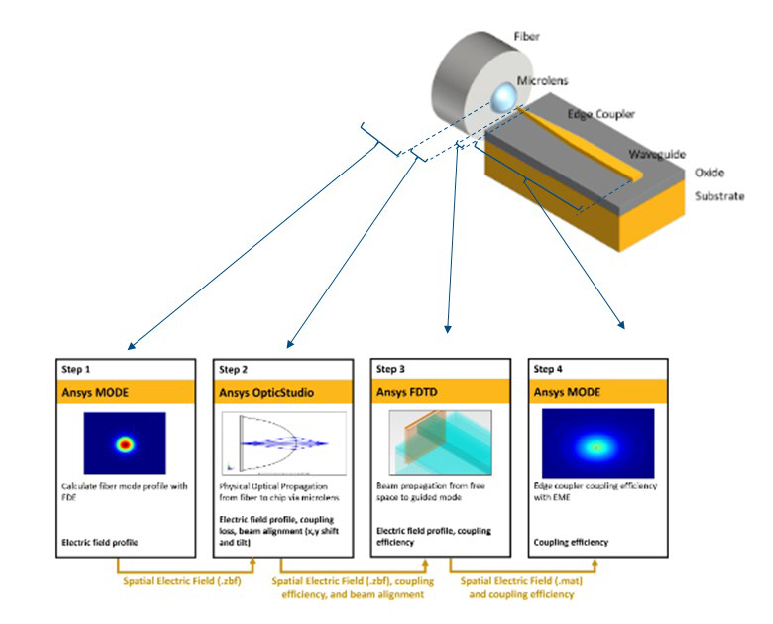
レーザー集光の高温レンズ歪みを克服するAnsys連携ソリューション
-
周波数応答解析×自動抽出で干渉チェックを高速化
-

直観的な操作で無線/デジタルフィルタの設計・最適化を支援する〜Ansys Nuhertz FilterSolutions〜
-
流体機器設計の新たな一歩
~Ansys Discoveryで加速する設計改革~
-
筐体の冷却性能を構想設計から見える化 (手戻りを削減できる)
~Ansys Discoveryで始める電気筐体製品の設計改革~
-
若手でもすぐに使えるリアルタイム解析 (勘と経験からの脱却)
~Ansys Discoveryによる30名規模メーカーの設計改革~
-
構想設計ですぐにリアルタイム検証 ~解析専任者ゼロでも使いこなせるAnsys Discovery~
~解析専任者ゼロでも使いこなせるAnsys Discovery~