CAEを学ぶ

垂直ひずみ(すいちょくひずみ)

英訳：normal strain

垂直ひずみは、下図のような棒において、変形した物体の元の長さに対する変化量の比という説明がなされることが多いです。

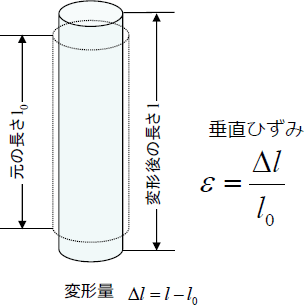
しかし、これは単軸状態の表現であり、より詳しく説明すると以下のようになります。

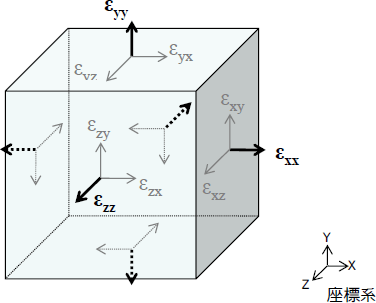
まず物体中に任意の直交座標系を定義し、その座標軸を法線方向とする微小な立方体領域を仮定します。この微小立方体において、座標系Y方向を法線方向とする面の法線方向ひずみはε _yy です。

ここで、添え字の1番目は作用面の法線方向を、2番目はひずみの作用方向を表します。

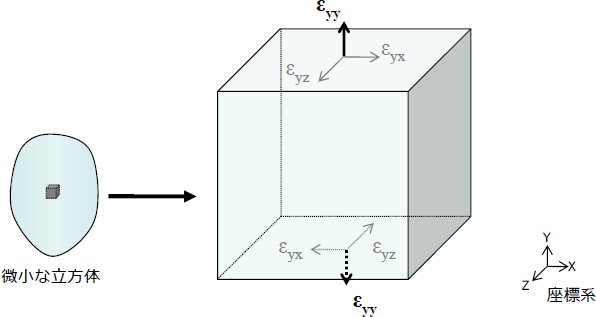
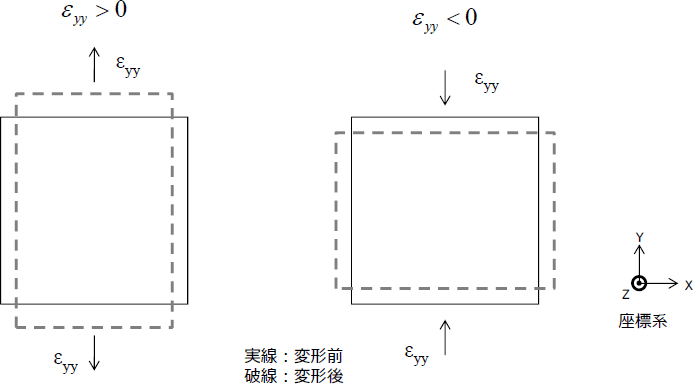
このひずみは、面内で下図のような変形が発生していると考えるとわかりやすいです。
なおε _yy が正の値の場合は引張り、負の値の場合は圧縮を表します。

同様にして、他の面についても考えると、面の法線方向に働くひずみは合計3成分（ε _x ,ε _y ,ε _z ）存在することになります。

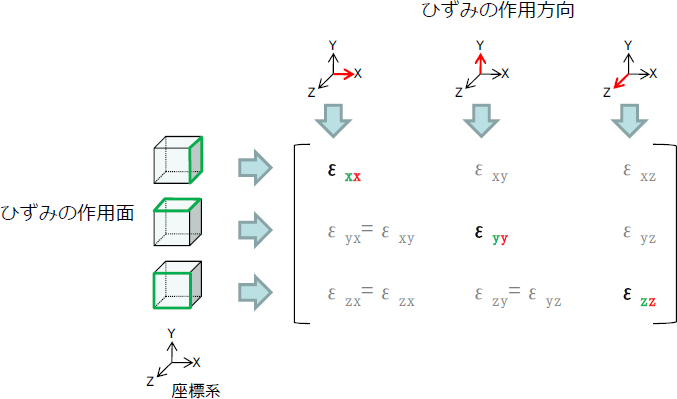
ここまでに得られたひずみを、添え字に注意してマトリクスの形でまとめます。
行にひずみの作用面、列にひずみの作用方向をまとめています。
このようにマトリクスでまとめたひずみを「ひずみテンソル」と呼びます。

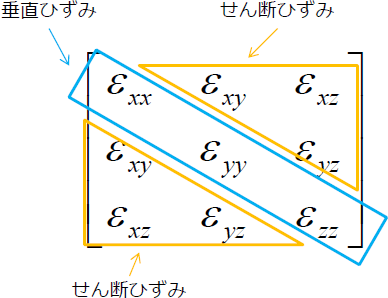
このひずみテンソルのうち、作用面と作用方向が一致する対角3成分が「垂直ひずみ」、残りの成分が「せん断ひずみ」です。

ひずみテンソルは、最初に定義した座標系を変更すると成分の値が変化します。
つまり、垂直ひずみ・せん断ひずみは座標系依存であり、CAEで垂直ひずみやせん断ひずみを評価する際には、どの座標系を基準に表示するかを決める必要があります。

なお、ここで定義したひずみは工学ひずみ（公称ひずみ）であり、微小変形が前提となっています。大変形を考慮した解析では真ひずみ（対数ひずみ）という異なる定義を使用します。

CAEでは微分形式でひずみをあらわすことが多くあります。
簡単のため1次元の微小な領域においてひずみを考えます。
元が微小な長さ⊿xで、左の点の座標はu _x 、右の点は⊿u _x 伸びてu _x +⊿u _x の位置に移動したとします。

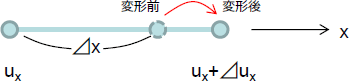
先の垂直ひずみの定義に従い、垂直ひずみは以下のように表されます。

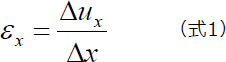
右の点の座標について、テーラー級数展開で二次以降の項を無視すると

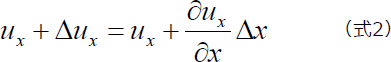
となります。従って、⊿u _x は

となります。これを先の式1に代入して微分形式の垂直ひずみが得られます。

3次元に拡張した場合も同様です。
まとめますと、微分形式の垂直ひずみは下式のようになります。

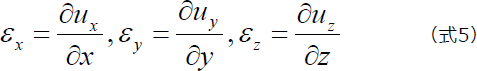
一般的に使用される単位

CAE用語辞典の転載・複製・引用・リンクなどについては、「著作権についてのお願い」をご確認ください。