CAEを学ぶ
ニュートンラプソン法(にゅーとんらぷそんほう)
英訳：Newton-Raphson method
ニュートンラプソン法とは、非線形方程式を線形解法の反復によって求める手法です。CAEでは、多くの非線形問題に対してニュートンラプソン法が用いられています。
以下、静的構造解析を例に説明します。
静的構造解析では以下のような連立方程式が作成されます。
ニュートンラプソン法では、線形の接線剛性マトリクス[K i T ]および復元荷重ベクトル{F i nr }を用いて、以下のように記述します。
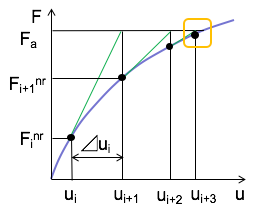
まず変位{u i }を仮定します。通常は、前ステップの収束解を用います。一番初めのステップでは0を用います。
この変位{u i }における接線剛性マトリクス[K
i T ]を計算します。この[K i T ]は材料の非線形性や幾何学的非線形を含めた、現時点での全体剛性です。
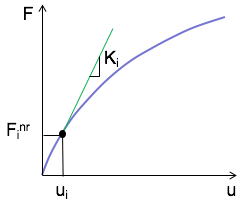
変位{u i }からひずみを計算し、ひずみから応力を計算します。
そして、応力から復元荷重ベクトルである{F i nr }が求められます。
負荷荷重ベクトル{F a }は与えた境界条件より既知ですから、（式2）より変位増分ベクトル{?u i }が求められます。
{u i
}に{?u i }を足して、次の近似{u i+1 }を求めます。
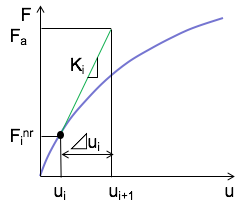
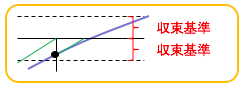
なお、復元荷重ベクトルと負荷荷重ベクトルの差、すなわち外力と内力の差である {F i nr }- {F a }を残差（残差力）と呼びます。
以上の手順を繰り返します。残差が指定した収束基準範囲内に収まれば、収束とみなします。（反復を繰り返しても収束基準範囲内に収まらない場合は、発散となります）
このようにして、ニュートンラプソン法では線形計算の繰り返しで非線形挙動を計算しています。
ここで示した反復のことを「平衡イタレーション」あるいは単に「イタレーション」と呼びます。
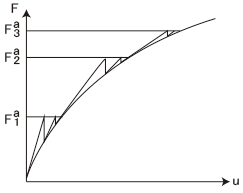
現実の非線形問題では一気に最終荷重まで計算出来ることは少ないため、荷重を小分けにして負荷していきます。
例えば最終荷重が100[N]であれば、最初の第1ステップではF a =F a
1 =10[N]として収束計算を行ない、これが収束したら次に第2ステップでF a =F a 2
=20[N]として収束計算を行なう、というように「収束計算→収束→次のステップ」の手順を繰り返して計算していきます。
上記の例では、各反復で接線剛性マトリクス[K i T ]が更新されるとしていました。このような方法を「フルニュートンラプソン法」と呼びます。非線形性の強い問題で推奨されます。
これに対して、1番目または2番目の反復でのみ接線剛性マトリクス[K i T
]が更新される方法を「修正ニュートンラプソン法」と呼びます。（当該ステップが収束して次のステップに移ったときには再度更新されます）
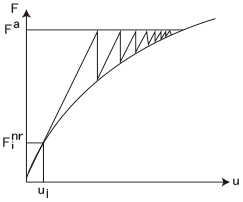
また、接線剛性マトリクス[K i T
]を（全ステップにおいて）更新しない方法を「初期剛性法」と呼びます。初期剛性法のイメージ図を以下に示します。
修正ニュートンラプソン法や初期剛性法は、非線形性の弱い問題に適しています。
Ansysにおける取扱い
- Ansysはニュートンラプソン法を問題の内容に応じて以下の3つから自動的に選択します。（手動選択も可能）
フルニュートンラプソン法
修正ニュートンラプソン法
初期剛性法
CAE用語辞典の転載・複製・引用・リンクなどについては、「著作権についてのお願い」をご確認ください。