CAEを学ぶ
自励振動(じれいしんどう)
英訳:self-induced vibration
自励振動とは、振動学的には「振動発生の原因である非振動的エネルギーが、その系内部の因子により振動的な励振エネルギーに変換されて発生し、自分でどんどん成長する振動」と定義されます。つまり、「与えているのはある一定の力だが、その一定の力がいつの間にか振動的な力に変化させられ、成長していく振動」です。
自由振動や強制振動に比べて複雑な振動で、発生原因やメカニズムは複雑ですが、機械設計においてしばしば問題となります。
代表的な例として、バイオリンの音やブレーキ鳴きがあります。バイオリンは弓でバイオリンの弦をこすり、弦が振動することにより音が発生します。
このような自励振動を解析する場合、複素固有値解析という手法が用いられます。
複素固有値解析では、固有値が実部と虚部からなる複素数となります。
複素固有値の実部と虚部の値の意味を1自由度系自由振動(一般粘性減衰系)モデルを使用して説明します。
下図のような1自由度粘性減衰振動系の運動方程式は(式1)のようになります。
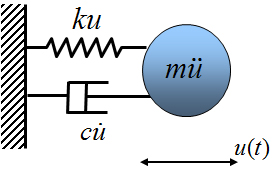 1自由度粘性減衰振動系
1自由度粘性減衰振動系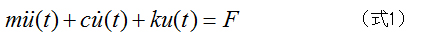
ここで、減衰自由振動の条件としてF=0とおく、つまり、減衰を考慮したマスのついたバネをある状態からリリースすることによって発生する定常振動状態の運動方程式は
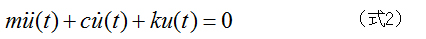
となります。
系は振動状態にあることから、変位u(t)を次のように仮定します。

これを(式2)に代入します。
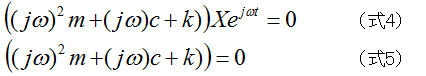
したがって、固有値jωは以下のように求められます。
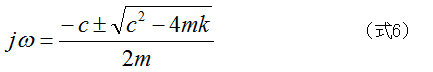
ここで、 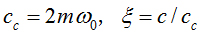 と定義すると
と定義すると
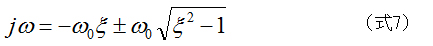
となります。
ω 0 は不減衰固有振動数、C c は臨界減衰係数、ξは臨界減衰比と呼ばれます。
ここで、ξの値により系がどのような振動状態になるかを考察してみます。
ケース1)ξ>1の場合
jω 1 , jω 2 は共に負の実数となります。
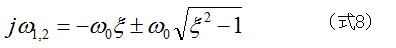
これを(式3)に代入すると、u(t)は一方的に減衰するだけであり、系は振動しないことが分かります。(過減衰状態)
ケース2)ξ=0の場合
jωは複素数となり、剛性と質量の関係からのみ決定される実固有値の解となります。
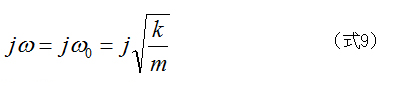
これを(式3)に代入すると、系は一定の振幅で振動することが分かります。(定常振動状態)
通常のモーダル解析は、このように減衰を無視(つまりξ=0)して計算しており、実固有値解析と呼ばれます。
ケース3)ξ<1の場合
jω 1 , jω 2 は共に複素数となります。
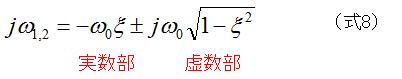
このように固有値が複素数となる場合、複素固有値解析が用いられます。
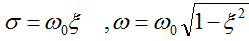 と定義すると
と定義すると
となります。これを(式3)に代入すると以下のようになります。
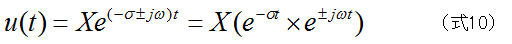
実部(real)は、減衰の早さを示します。
虚部(imag)は、振動の速さ(固有振動数)を示します。
ここで、 実数部が正(e σt ) となる場合、変位は時間と共に発散し、系は 不安定 となります。
つまり、複素固有値の虚部は固有振動数、実部は構造の安定性を意味します。
複素固有値解析を実施すると、下記のような各モードの実数部と虚数部の結果が得られます。
実部の値が正の場合、系が不安定(発散振動)となるため、自励振動が発生するモードおよび周波数となります。

以下の例は、Ansysで実施したブレーキ鳴き解析の、鳴き(自励振動)発生時のモード形状図です。パッドとディスクの両方が曲げ変形することによって鳴きが発生していることが分かります。

Ansysにおける取扱い
- Ansysでは複素固有値解析の解法として、減衰法、QR減衰法、非対称法を利用できます。
CAE用語辞典の転載・複製・引用・リンクなどについては、「著作権についてのお願い」をご確認ください。
関連キーワード
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

実測 × 解析で基板の熱変形問題を解決!基板反り現象の高精度シミュレーション
~エスペック(株)×サイバネットシステム(株)の連携ソリューション~
-

【全記事】CAEのあるものづくり vol.42
ユーザー様インタビュー記事7件を1冊に集約した保存版
-

誤差との上手なつきあい方 ~流体解析の計算誤差~ (完全保存版)
誤差との上手なつきあい方 前編・後編 を1冊にまとめた保存版 PDF
-

非線形解析の最大強度評価はAnsys LS-DYNAで解決!
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析で電子機器の信頼性向上
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

共振回避だけで終わらせない振動解析の進め方を解説(周波数応答・時刻歴まで)
~Ansys Mechanicalで実現する高度な製品開発~