フックの法則(ふっくのほうそく)

よく使われる工業材料は、弾性域内において垂直応力σと垂直ひずみεの間に比例関係が成り立つことが知られています。この関係をフックの法則と呼びます。
比例定数Eはヤング率と呼ばれます。

上式は一次元に単純化したものであるため、CAEではフックの法則を三次元に拡張して表現する必要があります。

まずX方向に垂直応力σ _xx が単独で作用したとします。X方向の垂直ひずみをε _xx とすれば、以下の関係が成り立ちます。（ここでは等方性材料を仮定しています）

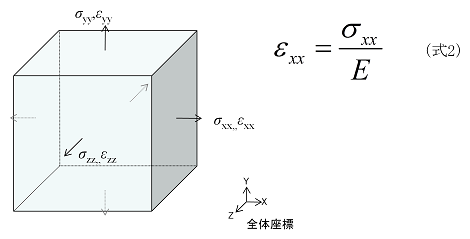
しかし、現実の材料ではX方向にだけ変形して、Y,Z方向にはまったく変形しないということはなく、必ず横ひずみを生じます。
Y方向の横ひずみをε _yy 、Z方向をε _zz とすると、ポアソン比νを用いて以下の関係が成り立ちます。（X方向に引張ならばとY,Z方向は圧縮となるため、符合に注意します）

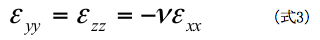
（式1）と（式2）より以下の関係が得られます。

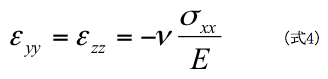
同様の方法で、Y,Z方向についても同様の関係を得ます。

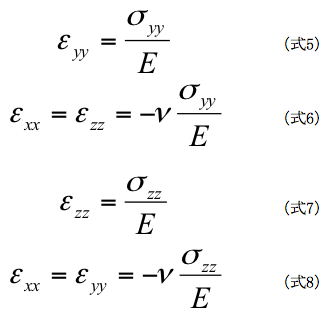
3軸方向に垂直応力が作用した場合、垂直ひずみと横ひずみが重ね合わせて発生します。
X方向のひずみε _xx は、式2,6,8を重ね合わせることにより、以下のようになります。

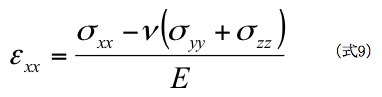
同様にY,Z方向のひずみは以下のようになります。

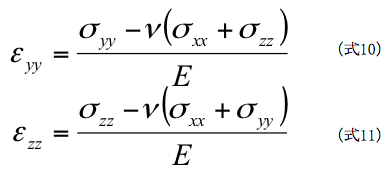
これらの式9,10,11は単軸の関係を三次元に拡張したもので、一般化されたフックの法則（generalized Hooke’s Low）と呼びます。

なお、せん断応力とせん断ひずみの関係は単軸せん断の場合と同様となります。

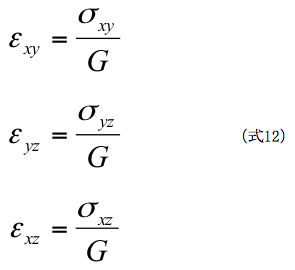
CAE用語辞典の転載・複製・引用・リンクなどについては、「著作権についてのお願い」をご確認ください。