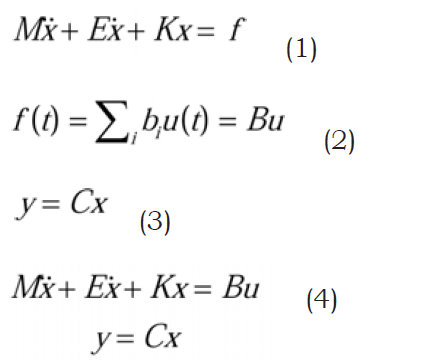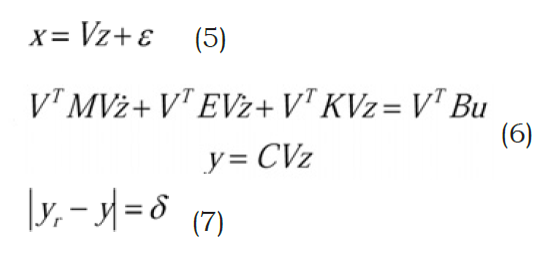CYBERNET

資料ダウンロード

構造解析

ROM (モデル低次元化) の概要


公開日2021年2月
CADFEM Infoplanerのこれまでの記事では、Model Reduction inside Ansysの実際の用途を複数紹介しました 。
ここでは、ROMを数学的観点で説明します。
資料をダウンロード

目次

  • ROMの式の定義
  • 射影としてのROM
  • エンジニアリングモデルの次元低減

2次系の時刻歴応答解析の場合に生成される常微分方程式

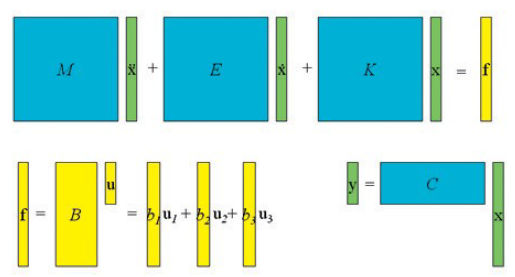
Ansysでは、解析前に計算領域を離散化します。これには、メッシングに加えて、解析対象の方程式系(まず各要素用、次に領域全体用)の生成が含まれます。2次系の時刻歴応答解析の場合、生成される常微分方程式は式(1)です。方程式は、質量マトリクスM、減衰マトリクスE、剛性マトリクスKの3つのグローバルマトリクスと、すべての自由度 (構造力学のUX、UY、UZのように、1つの節点が複数の自由度を持つ場合があります) を含む状態ベクトルx、および荷重で構成されます。伝熱問題の場合、質量マトリクスは存在せず (M = 0)、減衰マトリクスは熱容量マトリクス、剛性マトリクスは熱伝導率マトリクスです。この場合、節点数は自由度数に等しくなります (節点はTEMPのみ)。

xの次元を低減する数学問題として定義

式(1)の状態ベクトル (したがってマトリクス)の自由度数を低減し、システムレベルで高速解析することを目的とします。有限要素モデリングのレベルでは入力と出力を直接示す項が存在しないため、検討前にこれらを式(1)に導入します。最初に、時間依存の可能性がある荷重f(t)から開始します。これにより、荷重を定数ベクトルbiと時間依存関数u(t)の組み合わせに分離します 。 (式2)
システムレベルでは、必要なのは完全な状態ベクトルxではなく、その一部の情報のみです。これは、出力マトリクスCを使用して定義できます 。 (式3)
入力と出力の表記を使用して、式(1)を式(4) のように書き換えることができます。これで、ROMの式を、指定精度の範囲内で入力uと出力yの動的関係を保持しながらxの次元を低減する数学問題として定義できます。

射影としてのROM

形式上は、式(4)の状態ベクトルxのすべての自由度は独立していて、純粋な数学的操作によりそれらの一部を削除することはできません。理論的には、より高次の導関数を導入する、つまり特性マトリクス数を増加することで、xの自由度を低減できます。ただし、それにより計算の複雑性が軽減されることはなく、むしろ計算上の問題が増加します。これ以降、ROMは常に何らかの近似になります。複数のROM手法がありますが、すべての方法で共通して、式(5)で表現される射影の概念を使用しています。

PDF をダウンロード

関連情報

関連する解析事例

MORE

関連する資料ダウンロード

MORE

関連する解析講座・辞典

MORE

Contactお問い合わせ

お問い合わせ・資料請求

各種お問い合わせ・資料請求はこちら

見積り依頼

Ansys製品・CAE製品のお見積ご依頼はこちら

解析委託

各種解析のご依頼はこちら

Ansys、ならびにANSYS, Inc. のすべてのブランド名、製品名、サービス名、機能名、ロゴ、標語は、米国およびその他の国におけるANSYS, Inc. またはその子会社の商標または登録商標です。その他すべてのブランド名、製品名、サービス名、機能名、または商標は、それぞれの所有者に帰属します。本ウェブサイトに記載されているシステム名、製品名等には、必ずしも商標表示（(R)、TM）を付記していません。 CFX is a trademark of Sony Corporation in Japan. ICEM CFD is a trademark used by Ansys under license. LS-DYNA is a registered trademark of Livermore Software Technology Corporation. nCode is a trademark of HBM nCode.