Material Designer を使用したUD複合材料解析

2019年4月

目次

MDの結果の検証

この節では、MDの結果を、文献記載の測定値およびMDS-Liteで計算した弾性特性と比較検証します。これ以降の説明では、文献または競合製品の結果との差異を強調表示するため、結果を色分けして示しています(相対差が1、5、10パーセントを超えるものをそれぞれ青、緑、黄、20パーセントを超えるものを赤で強調表示しています)。

解析結果と競合ソフトウェアを使用した場合との比較

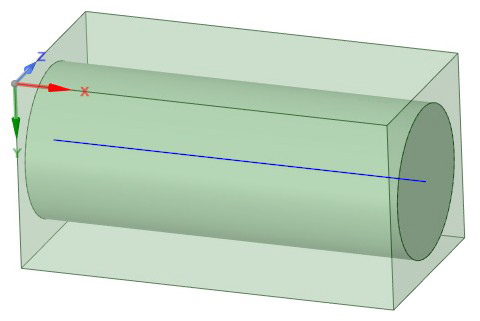
図1:MDを使用して調査したUD材料RVE (方形パターンの繊維)

MDを使用して、UD材料の代表体積要素(RVE)の弾性挙動を調査します。図1で示すように、マトリクス内の繊維が方形の一定のパターンで、周期境界条件がすべての計算で繊維軸に対して横方向であることを想定します。また、繊維の体積含有率を40パーセントとします。繊維とマトリクスの両方に等方性挙動を選択します。弾性特性に使用する値を表1に示します。

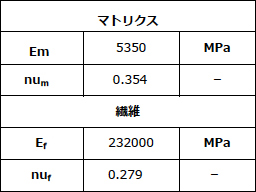
表1:繊維およびマトリクス材料の弾性特性(ヤング率(E) およびポアソン比(nu)、
以下、それぞれ添字fおよびmで表記)

マトリクスでの繊維の方形配置に対して有効なHalpin-Tsai式[1]を使用して、面内のせん断剛性G12および繊維に対して横方向の弾性剛性E2を求めます。単純なレベルルールを使用して、繊維方向の剛性E1およびポアソン比nu12を計算します。

下表では、解析結果を MD および MDS-Lite の値と比較しています。

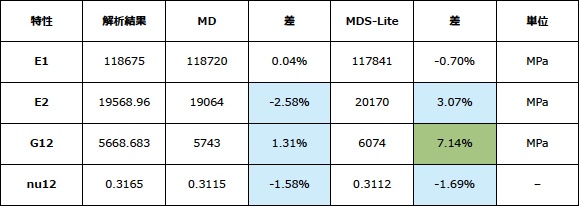
表2:MDおよびMDS-Liteによる解析予測の比較(方形パターンの繊維)

図2に示す、マトリクス内部で繊維が六角形パターンで配置されたさらに複雑なRVEのケースについて、MDとMDS-Liteを直接比較します。この比較の結果を表3に示します。

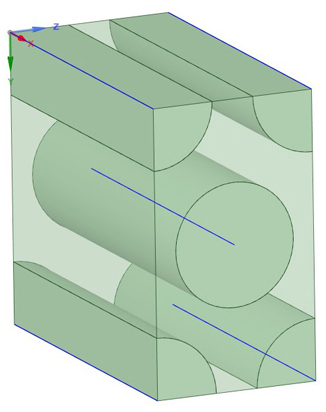
図2:MDを使用して調査したUD材料RVE(六角形パターンの繊維)

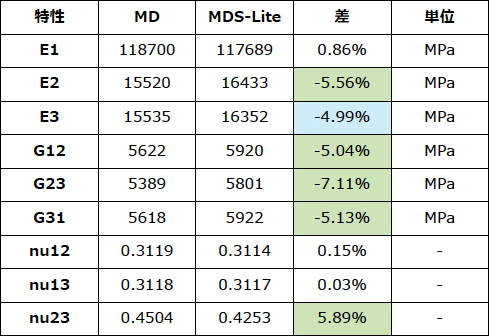
表3:MDとMDS-Liteの比較(六角形パターンの繊維)

文献の結果との比較

以下では、MDを使用して、プラスチックに埋め込まれたUD炭素繊維およびガラス繊維強化(いずれの場合も、以降の織物材料用の解析で使用されているヤーンUD材料を示しています)の文献記載結果が再現されています。下表では、fはマトリクス内の繊維の体積含有率を示します。

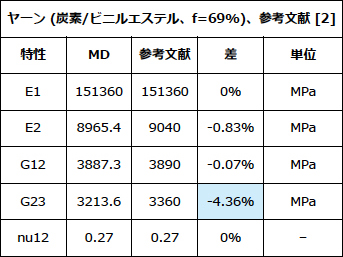表4:炭素繊維強化ポリマーの文献記載結果との比較

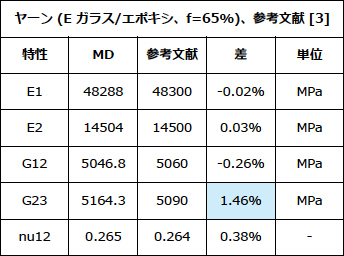表5:ガラス繊維強化ポリマーの文献記載結果との比較

UD複合材料の感度解析

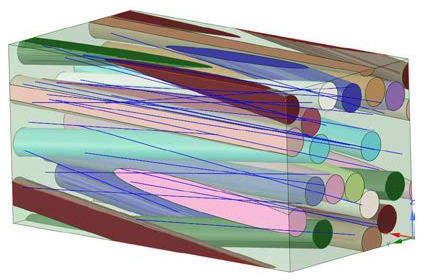
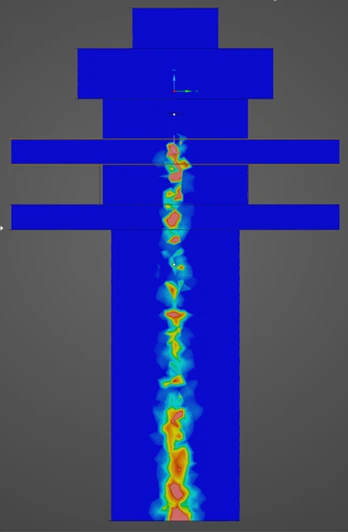
図3:マトリクス内での繊維の位置が不規則で、軸方向に対するアラインメントのずれが平均5度のUD材料のRVE

この節では、MDを使用して、炭素繊維およびガラス繊維のUDエポキシ複合材の弾性特性に対する繊維の位置およびアラインメントの不規則性の影響を調査します。また、この節の最後では、2つの結果の複合材の予測に基づく弾性挙動に対し、入力材料特性値の相対的な重要度を定量化します。図3は、繊維の軸方向に対するアラインメントのずれが平均5度で、マトリクス内で不規則に配置されているRVEを示しています。感度解析で考慮する炭素およびガラス繊維とエポキシマトリクスの基本特性を表6に示します。

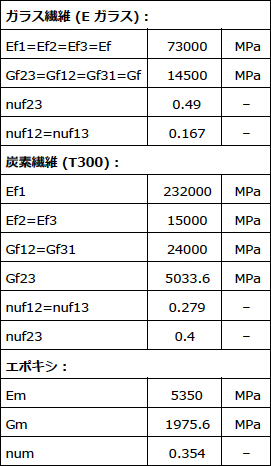
表6:以降の評価で考慮する炭素およびガラス繊維とエポキシマトリクス材料の弾性特性

直交異方性材料の定義を繊維で考慮します。エポキシ材料の基本特性は、マトリクスの直交異方性挙動に一致します。ただし、弾性係数、せん断弾性係数、ポアソン比が独立して変動することによって、特性計算結果にどのような影響があるのかを調査するため、モデルでは3つの独立パラメータがある直交異方性挙動を考慮します。比較中のRVEの基本特性では、繊維体積含有率が50パーセントの六角形繊維配置および周期境界条件が使用されています。

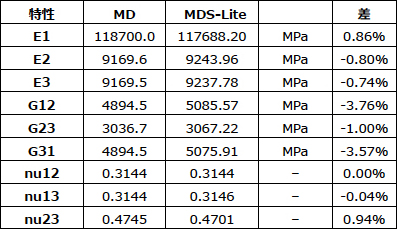
表7:基準RVEの炭素繊維UD予測(MDとMDS-Liteの比較)

表7および8では、炭素およびガラスのUD繊維強化の基準RVE(アラインメントのずれと繊維パターンの不規則性のいずれもなし)について、MDとMDS-Liteの予測を比較しています。…