資料ダウンロード
破壊力学について(2)
有限要素法による破壊力学解析

CAEのあるものづくり Vol.26|公開日:2017年5月
目次
- 有限要素法と破壊力学…二次元問題
- 直接法による応力拡大係数の計算 [1]
- エネルギー法による破壊力学パラメータの計算法
- 結び
有限要素法と破壊力学…二次元問題
今回は、有限要素法による破壊力学解析について、筆者が過去にサーベイした基本的内容からある種の独断も含めてご紹介しようと思います。有限要素法の破壊力学解析の目的を前回ご紹介した破壊力学パラメータ(応力拡大係数やJ積分)を求めることにあるとしましょう。つまり、破壊力学的評価は,破壊力学パラメータによって行いますから、有限要素法解析精度が悪くても破壊力学パラメータを必要な精度で計算できれば良いとも言えます。とは言え、変形状態、応力、ひずみ等が精度良く解析できていないと、破壊力学パラメータも精度良く求めることはできません。そこで、一般に、き裂先端近傍で細かい要素分割を与えます(図1)。しかし、その要求はどのようにして破壊力学パラメータを求めるかによります。一般に、有限要素法解析結果から破壊力学パラメータを計算する手法は大きく分けて二つの種類に分類することができます。「直接法」と「エネルギー法」です。
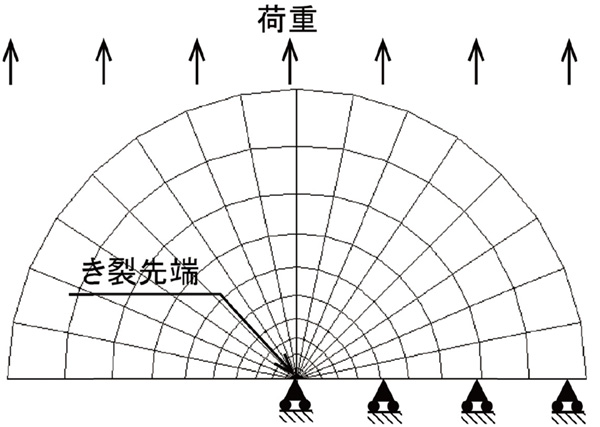 図1 き裂先端近くでの典型的な有限要素法解析モデル
図1 き裂先端近くでの典型的な有限要素法解析モデル直接法は有限要素法解析の結果として求められた、応力やひずみ、 き裂先端近傍の変位の値を、き裂の解にあてはめて応力拡大係数の値を推定するものです。一方、エネルギー法はき裂進展に伴うエネルギー量の変化からエネルギー解放率を計算します。それぞれについて計算法を紹介します。ただし、有限要素法解析結果からき裂パラメータを計算する場合、エネルギー法の方が高精度であると考えられています。これは、有限要素法の定式化が最小ポテンシャルエネルギーの原理や仮想仕事の原理のようなエネルギー原理に基づくことや、系全体のひずみエネルギーのようなマクロな量を精度良く解析できることによります。以下に具体的な計算手順を紹介します。
直接法による応力拡大係数の計算 [1]
前号の繰り返しになりますが、モードI問題でき裂先端近傍の応力場と変位は、き裂先端を原点とする極座標系(図2)により式(1)、(2)、(3)で与えられます。ただし、変位については平面ひずみ状態と平面応力状態で異なるので、三次元問題で特に注意が…
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

【全記事】CAEのあるものづくり vol.42
ユーザー様インタビュー記事7件を1冊に集約した保存版
-

誤差との上手なつきあい方 ~流体解析の計算誤差~ (完全保存版)
誤差との上手なつきあい方 前編・後編 を1冊にまとめた保存版 PDF
-

非線形解析の壁を突破するシミュレーション技術
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

共振回避だけで終わらせない実レベルの振動解析
~Ansys Mechanicalで実現する高度な製品開発~
-
吸入器内の粒子挙動を可視化する
~薬剤送達効率向上に向けた解析~