騒音問題の解決に役立つ振動音源の基礎

サイバネットシステムでは徳島文理大学 石原 国彦教授の協力のもと、実際の騒音対策に役立つ「実例を交えた音響工学講座」をご要望に応じてオンサイトで開催しています。講座では、振動理論、音響理論の基礎から応用までを深く解説し、音にまつわるトラブルと解決策の事例を紹介いたします。

以下に「実例を交えた音響工学講座」の一部抜粋版を掲載いたします。騒音問題の解決には音の性質や発生源について理解することが重要です。抜粋版では、音についての解説や音源として代表的な振動について解説します。ご興味をお持ちいただいた方は是非ページ下部からお気軽にお問い合わせください。

1．音の性質

1.1 音に関する基礎量

1.1.1 音波

音波とは、固体、液体、気体などの媒質中を伝わる弾性波です。ここでは主として空気中の音波について考えますが、液体中、固体中の音波についても触れることがあります。例えば音波の屈折では空気から水、空気から鉄への音波の伝搬を考えることになります。空気中の音波は疎密または濃淡の波、すなわち縦波だけしか存在しませんが、固体中では横波も存在します。
図１は音波の伝搬を説明するとき用いられるすだれです。粒子が集まった部分が圧力が高く、まばらな部分が圧力が低いことを示しています。そして、粒子自身はその場で振動しており、音波のエネルギーが伝搬します。すなわち粒子は伝搬しなく、エネルギーが伝搬することに注意しましょう。

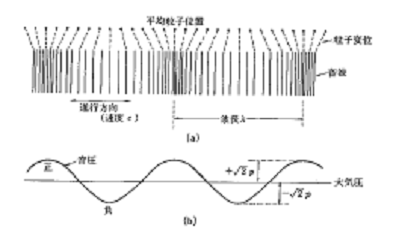図１　音の伝播状況

1.1.2 周波数と波長

周波数f（Frequency）は１秒間あたりのサイクル数で単位はHzです。波長λ（Wave length）は音波のある時間における空間の波の山から山、谷から谷の距離（長さ）をいい、単位はｍです。両者の間には音速ｃ（Sound speed）を介してｃ＝fλの関係があります。

1.1.3 音速

音速は音の伝搬速度であり、空気中では340m/s（常温）です。音速は温度のみで変化し、圧力には無関係です。音速は次式で与えられます。

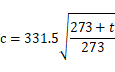
温度が50℃以下では近似式として次式が与えられます。

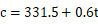
1.1.4 音の強さと音圧レベル

音の強さI（Sound Intensity）は単位面積あたり単位時間あたりに通過する音のエネルギーであり単位はJ/s/m2です。単位時間当たりのエネルギーはパワー（Power）で単位はW/m ² です。したがって音の強さの単位はW/m ² となります。
音圧レベルLp（Sound pressure level）は音の強さIまたは音圧ｐを用いて次式で与えられます。

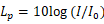
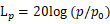
ここで 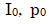はそれぞれ音の強さと音圧の基準値を示し、それぞれ 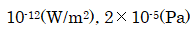です。これらの数値は覚えなければなりません。

これら２つの式は一見異なって見えるが、音の強さIと音圧ｐの間に

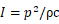
の関係があるので同一の式であることが容易に理解できます。
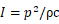の関係は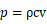
I=pvなる式から導かれます。

1.1.5 音響パワーと音響パワーレベル

音響パワー（Sound power）は音源固有の量で、音源が発する音のパワーでPで記述し、単位はW(ワット)です。P=ISでSは音源を囲む面積です。例えば音源が呼吸球であれば音波は球面状に伝搬するので音源から距離ｒの位置での音の強さは 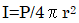となります。

1.1.6 音源から離れた点での音圧レベル

ある音源からｒｍ離れた位置での音圧レベルを知りたいという要求は多い。その場合は音源の音響パワーまたは音響パワーレベルが既知でないと求められません。また音源が置かれた状況、例えば空間に置かれている場合（自由空間）かもしくは地上に置かれた場合（半自由空間）があります。一般的には後者の場合が多いです。ここではまず自由空間の場合について説明します。

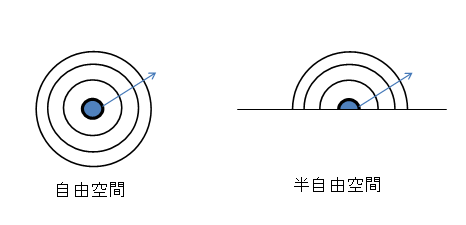図2　自由空間と半自由空間

音源パワーPが与えられた場合は、まずそれを音響パワーレベルL W に変換します。

P0は音響パワーの基準値であり、10 ^-12 (W)である。この値も覚える必要があります。
音は球面波として伝搬するのでｒ(ｍ)離れた点は半径ｒ(ｍ)の球面上にあります。その面積は 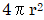であります。したがってその位置での音の強さIは

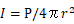
となります。
この式の両辺の対数をとり10倍すると
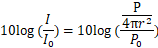となります。ここで 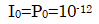です。

式(1)は定義より

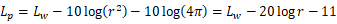
で表されます。それでは地上に置かれた半自由空間ではどうなるでしょうか？ 半自由空間では音波は半球面を形成されるので面積は 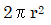となる。式(1)と異なる点は 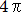が 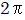となるだけです。したがって式(1)は 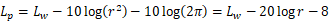となります。

半自由空間の音の強さは自由空間のそれの2倍でです。音の強さが2倍ということは3dBの違いが生じます。式(1)と(2)の最後の値の差が3dBであることに対応していることに注意しましょう。

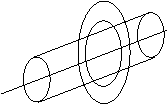
次に線音源ではどうなるでしょう？ 線音源では単位長さについて考え、円筒状に音波が伝搬します。音源パワーレベルLWは単位長さあたりのパワーP（W/m）を式(1)にしたがって変換します。線軸から垂直にｒ(ｍ)離れた長さ１ｍの円筒面の面積は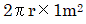となるため、円筒面上の点での音の強さIは

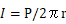
したがってこの式の両辺の対数をとり、10倍すると

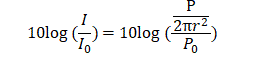
したがって定義により

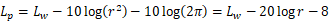
以上の説明から次のようにまとめられます。
(1) 点音源は-20log(r)で減少、線音源は-10log(r)で減少します。
(2) 自由空間の定数は-11, 半自由空間は-8で3dBの差があります。
(3) 点音源の減衰特性は-6dB/DD, 線音源のそれは-3dB/DD。
　　ここでDDは倍距離（Double Distance）を意味します。

1.1.7 騒音レベル

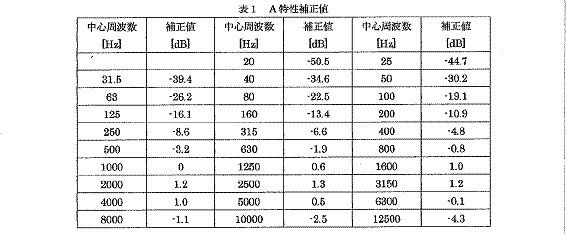
騒音レベルとは音圧レベルを補正したものです。その補正をＡ特性補正と呼びます。音圧レベルは音圧という物理量のdB値ですが、騒音レベルは感覚量であることに注意しましょう。人間の耳は周波数によって感度が異なるために、Ａ特性という補正を掛けて騒音レベルとしています。そのＡ特性の補正は表２に示されます。

1.2 音波の発生と音源の性質

前章では音の基本的な性質について述べました。以下では音の発生源（音源）について、解説していきます。音の主な発生原因は(1) 物体の振動、(2) 流れによる運動の二つが考えられます。前者は理解しやすいですが後者は比較的理解し難いです。以下では振動について解説していきます。

1.2.1 振動

ここでは物体の振動による音（Structure Borne Sound）について述べます。物体が振動すると物体表面にある空気粒子が励振され、振動エネルギーが伝搬します。したがって物体の振動振幅が大きいほど音の大きさが強くなります。特に物体が共振を起こした場合、振動振幅が大きくなるので問題となります。共振の有無を知るためには励振力の周波数と物体の共振周波数の両者を知らなければなりません。励振力の周波数は回転数などが分かれば容易に求めることができます。一方物体の共振周波数は単純なもの、例えば弦、棒、板などでは共振周波数、これを固有振動数とも呼びますが、式が表１のように与えられています。これらは寸法と材料特性、特にヤング率、それから境界条件が与えられれば求めることができます。一般には共振周波数を求めることは容易であると言われています。しかしそれは形状や境界条件が簡単なものに限られ、実際には特に境界条件が不明確な場合が多いので、ＦＥＭやＢＥＭなどの数値解析法を用いても難しいこともあります。

次に振動の理論について触れていきましょう。一般に構造物は連続体であり、その運動方程式は偏微分方程式で表されます。しかしながら振動で最も重要なのはあるモードでの共振であるので、それだけを取り出せば1自由度振動系を考えればよいです。ここでは1自由度振動系について述べます。
図１に1自由度振動系を示します。 平衡状態を基準にとり、質点の変位をxとすれば強制振動の運動方程式は次式で表されます。

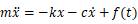
ここで、mは質量（kg）、kはばね定数（N/m）、cは減衰係数（N・s/m）、f(t)は外力（N）です。ここでf(t)=0、すなわち外力が無い場合は自由振動と呼ばれます。この振動では固有振動数と減衰比が振動特性として得ることができます。
自由振動について

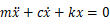
mで両辺を除すと

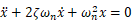
解を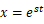とおき、式(1)に代入すると

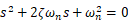
したがって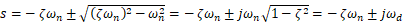

ここで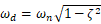であり減衰付固有円振動数と呼ばれる。式から減衰付固有振動数は減衰無し固有振動数より小さいですが、減衰比ζは実際は小さいのでほぼ同じと考えてよいです。

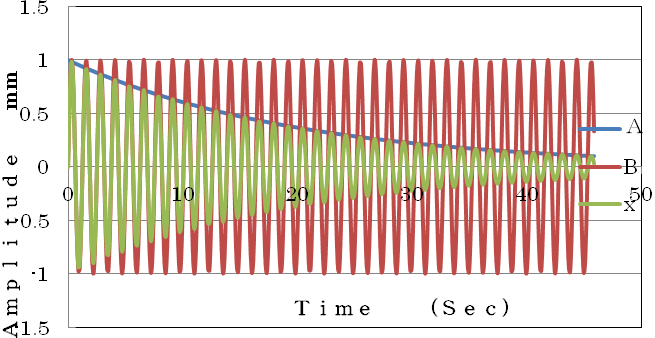
解は 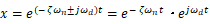となります。この式は図4緑グラフに示すように固有振動数がω_dで振幅が時間とともに減少する自由減衰振動を示しています。実機の振動特性であるω_dや減衰比ζは打撃試験を行い、そこから得られる自由減衰振動から求めることができます。

このときは対数減衰率δを測定することになるので、減衰比は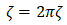で評価します。厳密には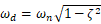の関係がありますが、ζが小さい場合は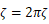としてよいです。

つぎに右辺に強制外力f(t)=Fsinωtが作用している場合を考えてみましょう。
解をx=Acosωt+Bsinωtと仮定し、式(1)に代入すると

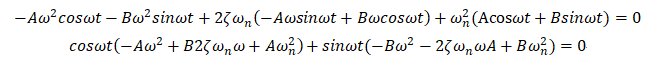
上の式が恒等的に成り立つためには

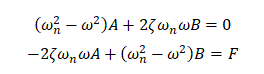
とならなければなりません。これはＡ，Ｂを未知数とする連立方程式であるので解けば、Ａ，Ｂは以下のように求めることができます。


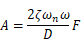
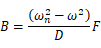
ここで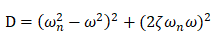です。

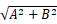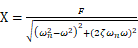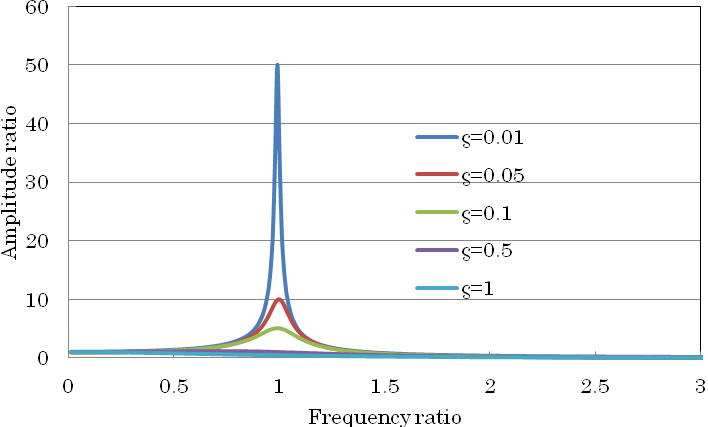
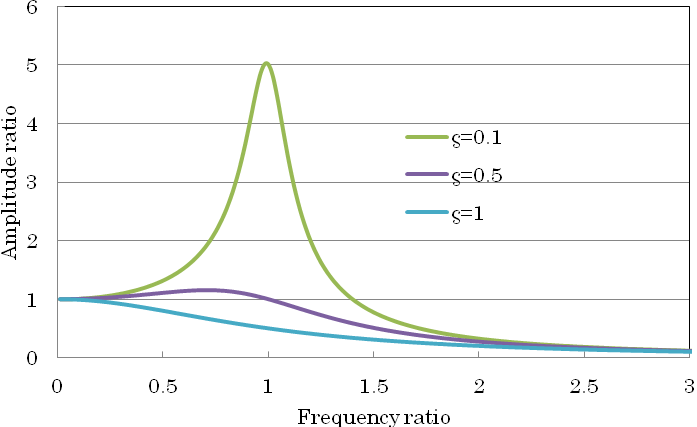
解の振幅はであるから位相φは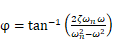となります。一般には力に対する振幅として振動数比（加振振動数/固有振動数）に対して示されます。これを共振曲線とも呼んでいます。その図を減衰比をパラメータとして図5に示します。

ここで解をと置けないのはなぜでしょうか？減衰が無い場合は加速度が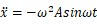であるため、sinωt が次のように両辺で消すことができ、容易に解を求めることができます。以下にその過程を示します。

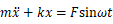
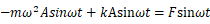
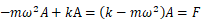
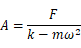
として振幅Ａが求まる。ところが前述した減衰がある場合は、

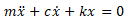
において、左辺第1項と第3項は減衰無のとき述べたように右辺の力の項でsinがありますが、第2項でcosが生ずることから、減衰がある場合はsinとcosの両方で解を著わす必要があります。この点を注意しましょう。

ここで示した解法より最も簡便な方法として複素数を用いる手があります。すこしだけ数学ができる人には簡単ですので、紹介します。強制振動の運動方程式を

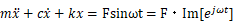
とおきます。なぜならオイラーの式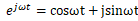から明らかであるからです。
解を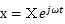と仮定します。このときＸは複素数です。
したがって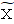と記します。

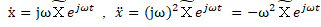
であるからこれらを式(*)に代入すると

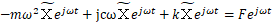
これより

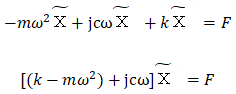
したがって

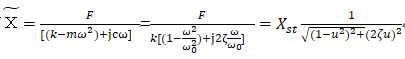
となり、式(1)と一致します。

2.おわりに

本抜粋版では「実例を交えた音響工学講座」の内容の一部を抜粋し、音の性質、基礎量および振動による音を例にした音の発生と音源について紹介しました。「実例を交えた音響工学講座」ではこの続きをより深く、詳細にご紹介いたします。以下に「実例を交えた音響工学講座」のアジェンダを記載いたしますので、ご興味をお持ちの方は是非お問合せフォームからお問い合わせください。