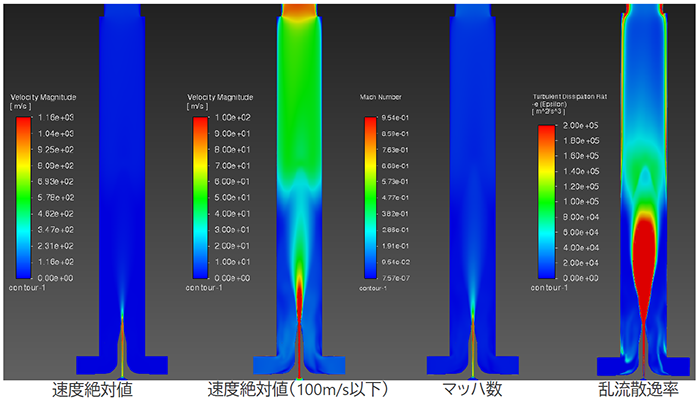
解析事例
先進的な要素定式化を用いた繊維系複合材料の大ひずみ数値材料試験
複合材料モデルおける数値材料試験の収束問題について
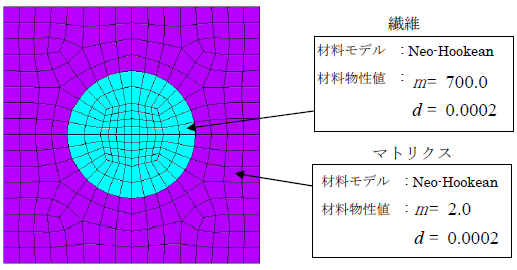
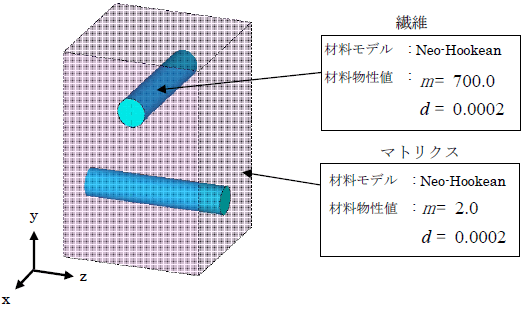
図1 は紙面垂直方向に繊維が配向している一方向強化の複合材料をモデル化したものです。繊維とマトリクスの間には、3 桁程度の剛性差があります。
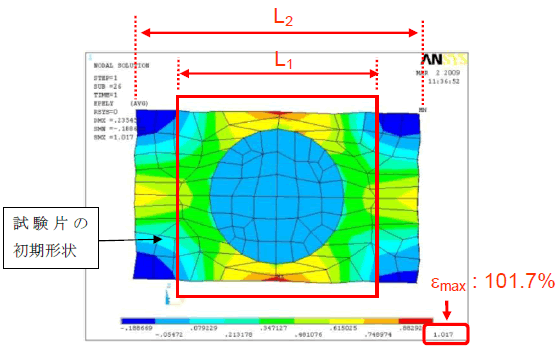
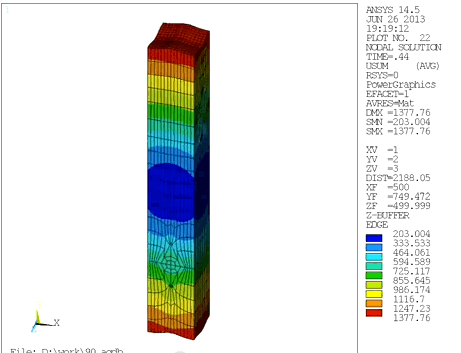
このモデルに対して繊維に対して直交方向に数値材料試験を実施したときの引張方向成分の弾性ひずみの分布を図2 に示しました。マクロひずみ30%までの試験を実施しておりますが、ミクロスケールのひずみ分布を観測すると、繊維近傍では100%以上の引張ひずみが、遠方では-10%程度の圧縮ひずみが発生していることが確認できます。このように剛性差の大きいモデルに対して数値材料試験を実施すると、たとえ単純な形状であっても、モデル内に極めて大きなひずみの勾配が局在化し、要素崩壊により解析が進められないケースが頻繁に発生してしまいました。
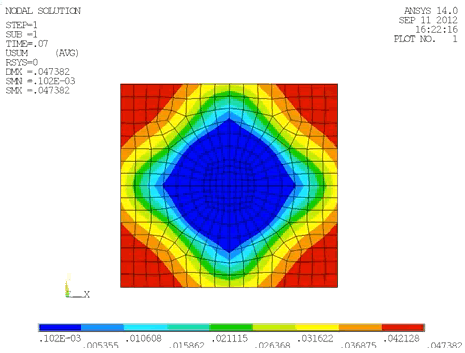
図3 は、要素崩壊の様子をアニメーション表示したものです。
新要素による数値材料試験の結果比較
1 方向強化繊維複合材料
Multiscale.Sim4.1 から新しく実装されたHannover 大学のReese らによる先進的な要素定式化 ※1 を用いて図1 のモデルに対して一軸引張試験を実施し、Ansys 既存の低次ソリッド要素と結果を比較したものをアニメーションにしました(図4)。既存の要素タイプでは、約30%程度マクロひずみで要素崩壊による解析終了が避けられませんが、新要素では100%以上のマクロひずみを与えても安定して解析を実施することができました。
±90 度配向の繊維系複合材料
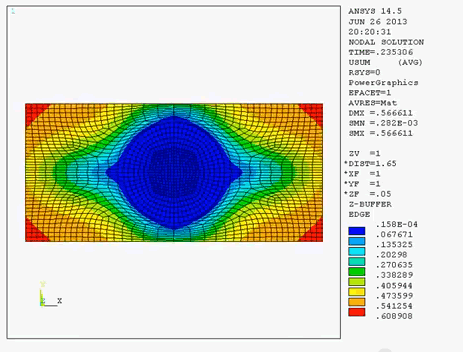
同様の比較検証を図5 に示した±90 度配向のモデルに対して実施しました。繊維、マトリクスの材料物性値は図1 と同様の値を採用しました。繊維の配向していないy 方向に対して単軸の引張試験を実施しました。
図6は、既存要素と新要素に対してそれぞれ変形の様子を示したものです。既存要素ではマクロひずみ40%で要素崩壊が発生したのに対し、新要素ではマクロひずみ400%にいたるまで非常に安定して解析を行うことができました。
※1 S. Reese, P. Wriggers; "A stabilization technique to avoid hourglassing in finite elasticity"; International Journal for Numerical Methods in Engineering; Vol. 48, 79-109 (2000)
関連キーワード
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

実測 × 解析で基板の熱変形問題を解決!基板反り現象の高精度シミュレーション
~エスペック(株)×サイバネットシステム(株)の連携ソリューション~
-

【全記事】CAEのあるものづくり vol.42
ユーザー様インタビュー記事7件を1冊に集約した保存版
-

誤差との上手なつきあい方 ~流体解析の計算誤差~ (完全保存版)
誤差との上手なつきあい方 前編・後編 を1冊にまとめた保存版 PDF
-

非線形解析の最大強度評価はAnsys LS-DYNAで解決!
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析で電子機器の信頼性向上
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

共振回避だけで終わらせない振動解析の進め方を解説(周波数応答・時刻歴まで)
~Ansys Mechanicalで実現する高度な製品開発~