解析事例
電子機器はんだ接合部の熱疲労寿命評価 〜特異場パラメータを用いた評価〜
劉 継紅 様
はじめに
長期間の温度変化の繰り返しにより、電子機器はんだ接合部近傍においてき裂が発生しやすく、電子機器の熱疲労寿命に大きな影響を及ぼすことが一般に知られています。現在、電子機器はんだ接合部の熱疲労寿命は主にパワーサイクル試験や温度サイクル試験などの試験的な手法で評価されていますが、開発の効率化と完成度向上を図るため、解析によるはんだ接合部の熱疲労寿命の評価が強く望まれます。
今まで電子機器はんだ接合部の熱疲労寿命評価に関する研究が幾つか発表されました(1)。これらの研究では、異材結合によるはんだ接合部近傍の応力場の特異性を避けるため、ある代表点の最大応力振幅または最大ひずみ振幅を用いてはんだ接合部の熱疲労寿命を評価しました。この手法ははんだ接合部が相似した構造を有し、応力またはひずみに同様な計算精度を確保した場合は実用性がありますが、代表点の選定に任意性や試行錯誤を伴い一般化するには不向きです。
異材結合のため、はんだ接合部近傍における応力場は特異性を有します。一般的に言えば、応力特異場の挙動は、特異場オーダーと特異場強さ係数によって完全に記述することができます。そこで、本報では、はんだ接合部近傍の応力特異場パラメータを用いて電子機器はんだ接合部の熱疲労寿命の評価を試みます。具体的には、まず、はんだの材料物性を材料試験により把握します。次に、パワーモジュールを対象に温度サイクル試験条件下におけるはんだ接合部近傍の応力特異場パラメータをFEM解析で求めます。また、応力場特異パラメータと疲労試験結果を疲労則により関連付け、はんだ接合部の熱疲労寿命評価式を作成します。最後に、今後の課題等について考察します。
はんだの材料物性
はんだ接合部の熱疲労寿命評価では、温度荷重によるはんだ接合部近傍の応力特異場を精度よく解析することが重要です。はんだ材料は融点が低く通常の使用温度においてもクリープ現象を示すため、材料物性、とくに弾性率と降伏応力(耐力)の温度依存性およびクリープ構成式を正しく把握しなければなりません。本節では、材料試験の結果に基づいて鉛はんだ(Pb-5Sn)と鉛フリーはんだ(Sn96.5Ag3.0Cu0.4)の材料物性を明らかにします。
はんだの弾性率と降伏応力
材料試験では、試験片の載荷部の影響を避けるため、ひずみは試験片の標点間変位の公称値から算出するのではなく試験片中心の両側に貼り付けたひずみゲージを用いて測定します。はんだの弾性率と降伏応力を求める静的引張り試験は変位制御による加載法で行われ、また、加載速度の違いによる試験結果への影響についても検討します。
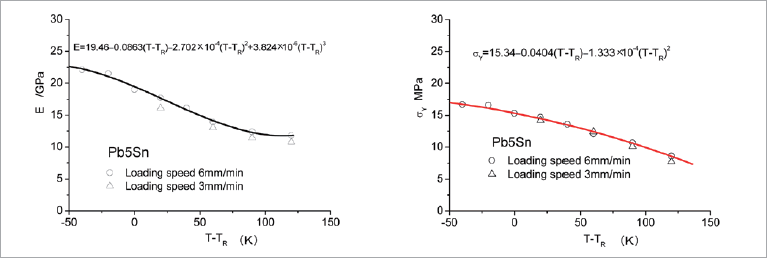
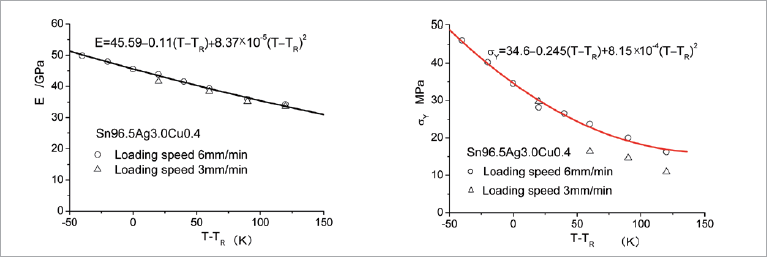
温度の違いによる鉛はんだと鉛フリーはんだの弾性率および降伏応力の変化、ならびにはんだの弾性率と降伏応力の近似式をそれぞれ図1と図2に示します。これによると、はんだの弾性率と降伏応力が温度の上昇に伴い低下し、顕著な温度依存性を有することが明らかになりました。また、鉛はんだは弾性率と降伏応力が加載速度の影響を受けないのに対し、鉛フリーはんだは弾性率が加載速度の影響を受けないが、降伏応力が加載速度の影響を受けることが読み取れます。これは、鉛フリーはんだは降伏応力が高く、また高温高応力状態での引張り試験結果がクリープ変形の影響を受けやすいことによると推測されます。よって、クリープ変形の影響を避けるため速い加載速度(6.0mm/min)での試験結果が望ましいと考えます。
はんだのクリープ構成式
はんだのクリープ試験は力制御による加載法で行われます。本節では、異なる応力状態と温度条件下でのクリープ曲線の定常クリープ域から求めたクリープひずみ速度と対応する応力を用いてはんだのクリープ構成式を作成します。はんだのクリープ構成式は、低応力状態では線形粘性型、高応力状態では双曲線型の関数式で表現することができます(2)〜(3)。
クリープ試験結果に基づいて作成した鉛はんだのクリープ構成式は式(1)で与えられます。
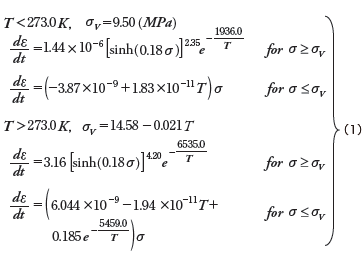
ここで、温度T (K)の適用範囲は 233.0K から393.0K まで、σv (MPa)は線形クリープ限界応力です。鉛はんだのσv は低温時に温度T に依存しませんが、常温以上になると温度T の関数となります。鉛はんだの応力とクリープひずみ速度の関係を両対数形式で図3に示します。これによると、式(1)のクリープ構成式は鉛はんだの試験結果を精度よく表現できることが読み取れます。クリープ試験結果に基づいて作成した鉛フリーはんだのクリープ構成式は式(2)で与えられます。
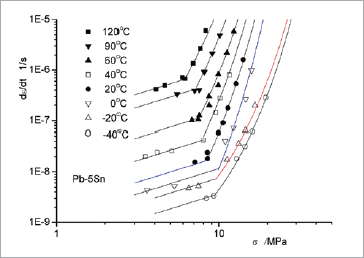
図3 鉛はんだの応力とクリープひずみ速度の関係
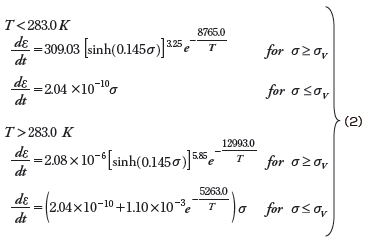
鉛フリーはんだの線形クリープ限界応力σv (MPa)は温度T (K)の関数として次式で近似的に与えられます。
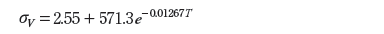
鉛フリーはんだの応力とクリープひずみ速度の関係を両対数形式で図4に示します。これによると、×印した20.0℃での試験結果に不適切と思われる箇所がある以外、式(2)のクリープ構成式は鉛フリーはんだの試験結果を精度よく表現できることが読み取れます。×印箇所では応力が低く、クリープひずみ速度が小さく試験誤差が大きく現れたと推測されます。
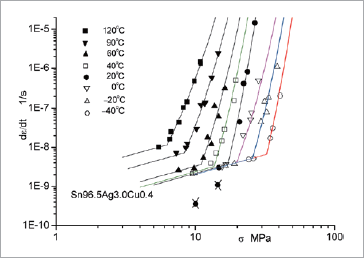
図4 鉛フリーはんだの応力とクリープひずみ速度の関係
はんだ接合部の応力特異場
本節では、パワーモジュールを対象に温度サイクル試験条件下(-40.0℃〜80.0℃〜-40.0℃)におけるはんだ接合界面端近傍の応力特異場パラメータをFEM解析で求めます。温度サイクル試験条件の略図を図5に示します。温度サイクル試験では、パワーモジュール全体を環境試験炉に投入し、規定の温度サイクルを繰り返します。規定の温度サイクル数が経過した後に、チップ端の熱また電気抵抗の増加率を測定し故障サイクル数の判定を行います。
はんだ接合界面端近傍の応力特異場パラメータを精度よく求めるには、図6に示した手順を踏んだズーミング法で応力解析を行います。詳細な解析手順は以下に示します。なお、解析には汎用FEM構造解析ソフトウェアAnsysを使用します。
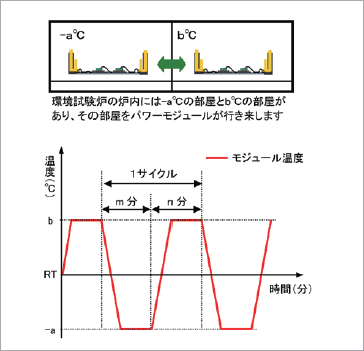
図5 温度サイクル試験条件の略図
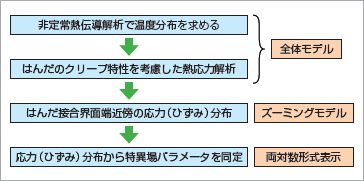
図6 はんだ接合界面端の応力特異場パラメータの計算流れ
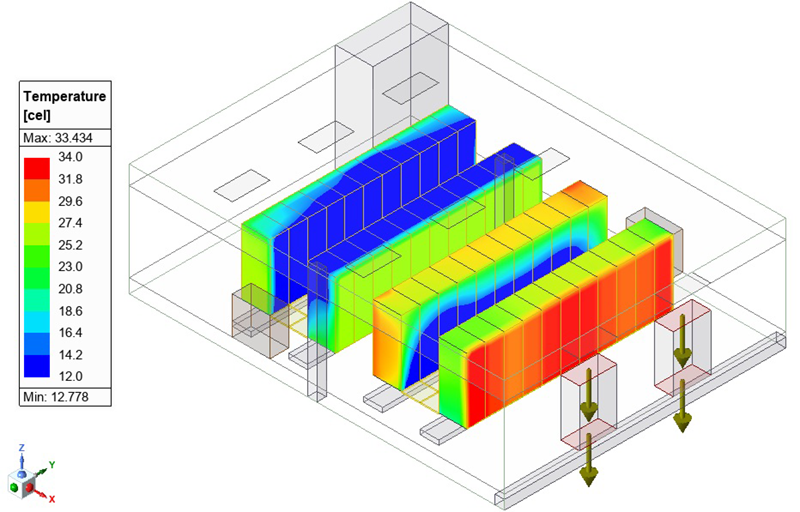
1) 図7に示した全体解析モデルで非定常熱伝導解析を行い、パワーモジュールにおける温度分布を求めます。解析では、パワーモジュールの表面と周囲(試験炉内)環境との間に自然対流条件を指定します。
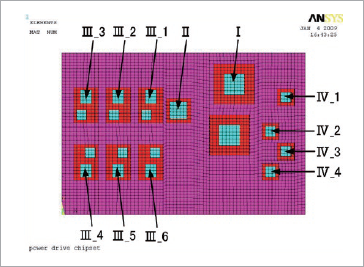
図7 パワーモジュールの全体解析モデル
2) 全体解析モデルで非線形熱応力解析を行い、パワーモジュールにおける熱応力分布と変形の様子を求めます。解析に際しては、パワーモジュールに剛体変位が発生しないように拘束条件を付与し、上記1)の非定常熱伝導解析で求めたパワーモジュールの温度分布を温度荷重条件として用います。また、はんだについては、前節で明らかにした弾性率と降伏応力の温度依存性およびクリープ特性を解析に考慮します。
3) 図8に示したズーミング解析モデルを用いてチップのはんだ接合界面端近傍の詳細な応力分布とひずみ分布を解析します。解析では、全体解析モデルでの解析結果に基づいた変位境界条件および温度荷重条件を線形補間してズーミング解析モデルに付与します。
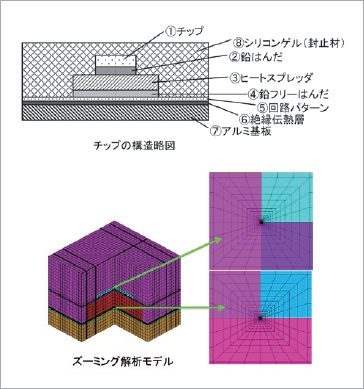
図8 チップの構造略図およびズーミング解析モデル
4) チップ構造は図8に示したように異なる機械特性と熱特性をもつ多層構造になっています。チップ①と鉛はんだ②の接合界面端(E12と表示)および鉛フリーはんだ④と回路パターン⑤の接合界面端(E45と表示)に特異応力場が存在します。はんだ接合界面端近傍の特異応力場および特異ひずみ場は式(3)のように表現することができます。
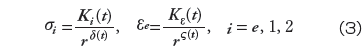
ここで、t は時間を、i = e, 1, 2 はそれぞれ相当応力、垂直応力とせん断応力を表します。ひずみについては相当ひずみのみを考えます。特異場オーダー
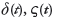 と特異場強さ係数Ki (t), Kε(t) はそれぞれ時間t
の関数で、数値解析で求めることができます。具体的には、はんだ接合界面端近傍の応力分布またはひずみ分布を両対数形式で表示した場合に得られた線形的な線図の傾斜が応力またはひずみの特異場オーダーになります。対応する応力またはひずみの特異場強さ係数は、該当線図の常数部からまたは外挿法等で求められます。なお、疲労寿命評価では、最大応力または最大相当ひずみの特異場パラメータの振幅が重要であるため、本報では、温度サイクル試験条件下の最大・最小応力状態または最大・最小ひずみ状態での特異場パラメータに注目します。
と特異場強さ係数Ki (t), Kε(t) はそれぞれ時間t
の関数で、数値解析で求めることができます。具体的には、はんだ接合界面端近傍の応力分布またはひずみ分布を両対数形式で表示した場合に得られた線形的な線図の傾斜が応力またはひずみの特異場オーダーになります。対応する応力またはひずみの特異場強さ係数は、該当線図の常数部からまたは外挿法等で求められます。なお、疲労寿命評価では、最大応力または最大相当ひずみの特異場パラメータの振幅が重要であるため、本報では、温度サイクル試験条件下の最大・最小応力状態または最大・最小ひずみ状態での特異場パラメータに注目します。
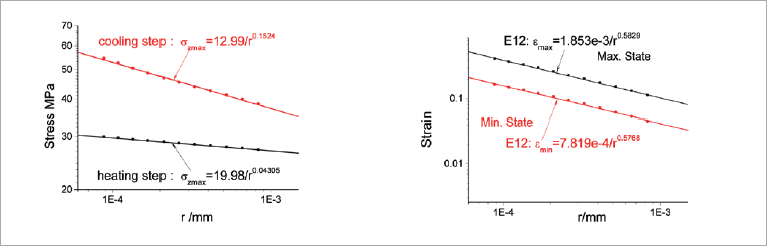
一例としてE12はんだ接合界面端近傍における最大応力状態時の応力分布と最大ひずみ状態時のひずみ分布を図9に示します。これによると、両対数形式表示の応力分布とひずみ分布ははんだ接合界面端近傍において良好な線形性を示す直線となることが読み取れます。この直線から応力場とひずみ場の特異場パラメータを高精度に同定することができます。
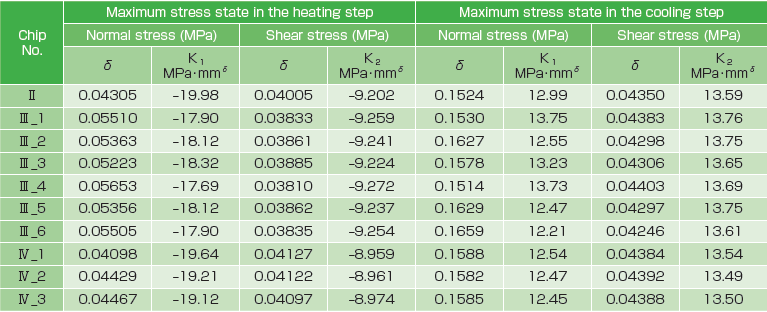
後述するパワーモジュールチップのSEM観察によれば、温度サイクル試験では、E12はんだ接合界面端近傍からき裂が開始・進展することが明らかになりました。そこで、本節では、温度サイクル条件下におけるE12はんだ接合界面端近傍の応力場とひずみ場の特異場パラメータを計算し、表1と表2にまとめました。これらの特異場パラメー タを用いてE12はんだ接合界面端近傍の最大応力状態または最大ひずみ状態を完全に記述することが可能となります。また、温度サイクル試験では、E12はんだ接合界面端の垂直応力が周期的に圧縮状態から引張り状態に変化することが表1から読み取れます。
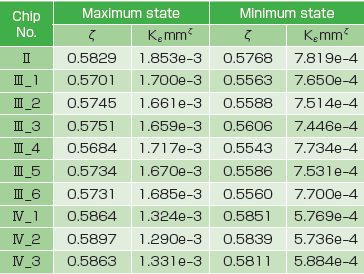
Table 2. Singular strain field parameters for E12 interface edges under thermal cycles
温度サイクル試験
本節では、図5に示した温度サイクル試験条件下におけるパワーモジュールの熱疲労試験結果を述べます。温度サイクル試験では、パワーモジュールは環境試験炉内で-40.0℃と80.0℃の温度環境にそれぞれ30分ずつ保持する温度サイクルを繰り返します。本報では、温度サイクル数と温度サイクル10回ごとに測定したチップ端の電気抵抗変化率との関係線図からチップ端の電気抵抗変化率が急激に上昇する時点での温度サイクル数を読み取り、それをチップの熱疲労寿命とします。また、チップ断面のSEM写真(図略)観察から、チップII(図7参照)の場合を除いて、き裂がE12はんだ接合界面端近傍から開始・進展することが確認されました。
上記手法で求めた温度サイクル試験条件下におけるパワーモジュールの各チップの熱疲労寿命を表3に示します。これによると、各チップの位置や形状が異なるにもかかわらず、チップII以外のチップの熱疲労寿命は約1000サイクルであることが読み取れます。これは、温度サイクル試験条件下では、各チップのE12はんだ接合界面端近傍の応力場またはひずみ場の特異性パラメータがほぼ同等であることを意味すると推測されます。なお、チップIIについては、解析結果からはE12はんだ接合界面端近傍からき裂が開始すると思われますが、SEM写真観察からはき裂がE45近傍から発生することが確認されました。計算結果とSEM観察結果の違いの原因はE45近傍に初期欠陥の可能性があったと推測されます。
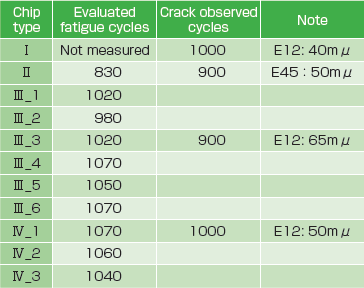
Table 3. Evaluated fatigue lives of chips in power modules under thermal cycles
はんだ接合部の熱疲労寿命評価
本報では、温度サイクル試験は-40.0℃〜80.0℃〜-40.0℃の温度サイクルで実施しました。-40.0℃と80.0℃の温度条件下におけるはんだ接合界面端近傍の特異場オーダーと特場強さ係数は異なります。また、温度サイクル試験では、はんだ接合界面端の垂直応力が周期的に圧縮状態から引張り状態に変化し、き裂を引き起こす要因となっていると思われます。
疲労則
疲労破壊問題では、応力またはひずみの振幅が重要な役割を果たすことが知られています。界面端近傍の特異場では、最大応力振幅または最大ひずみ振幅は次式のように表現することができます。すなわち、
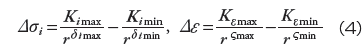
ここで、 i は垂直応力またはせん断応力を表します。r は特異点からの距離です。式(4)より最大応力振幅または最大ひずみ振幅を求めるには、次の特異場パラメータが必要となります。すなわち、
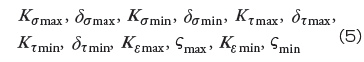
上記のパラメータは数が多く、そのまま使用して疲労則を作成するのが困難でかつ不便です。そこで、界面端特異点近傍の単位長さの平均応力振幅に関する理論的な考察から、上記のパラメータは次の三つにまとめられます。
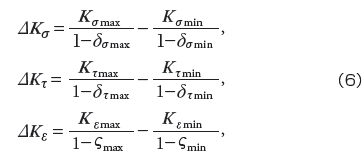
ここで、 ΔKσ, ΔKτは多軸応力状態の影響を、ΔKεはひずみサイクルを表します。この三つのパラメータを用いて、幾つかの疲労則の理論式が考えられます。経験的に界面端近傍の疲労破壊は主に界面端近傍における表面力(traction)振幅に左右されることが知られています。一般に界面端近傍の表面力振幅は多軸応力状態の変化を包含することができます。界面端近傍の疲労寿命予測には次の四種類の疲労則が考えられます。
ひずみ支配型疲労則(Strain controlled fatigue law)

応力支配型疲労則(Stress controlled fatigue law)
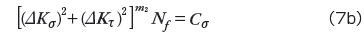
加速型疲労則(Accelerating fatigue law)
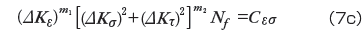
累積型疲労則(Accumulating fatigue law)
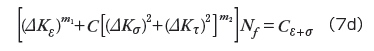
上記疲労則の定数は温度サイクル試験またはパワーサイクル試験の結果により同定されます。破壊理論から考えると、上記疲労則の右辺の定数は疲労試験の繰り返し比(cyclic ratio)に依存し、温度サイクル試験とパワーサイクル試験とでは異なりますが、左辺の指数は材料定数で疲労試験の種類に依存しません。どの疲労則がはんだ接合界面端近傍の疲労寿命評価に最も適しているかについては、界面強度の特性または疲労試験結果への適合精度により決まります。
パワーモジュールの疲労則
上述のSEM写真の観察結果によれば、温度サイクル試験では、パワーモジュールの疲労破壊はE12はんだ接合界面端近傍から開始することが一般的です。そこで、ここでは、E12はんだ接合界面端近傍からの疲労破壊の評価式を作成します。表1と表2に示した特異場パラメータと表3に示した熱疲労試験結果を式(7)の疲労則に代入しフィッティングすると、温度サイクル試験条件下におけるパワーモジュールの疲労寿命評価式は次のように与えられます。
ひずみ支配型疲労則

応力支配型疲労則
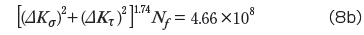
加速型疲労則
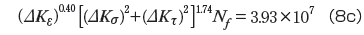
累積型疲労則
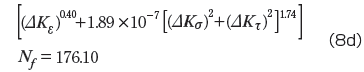
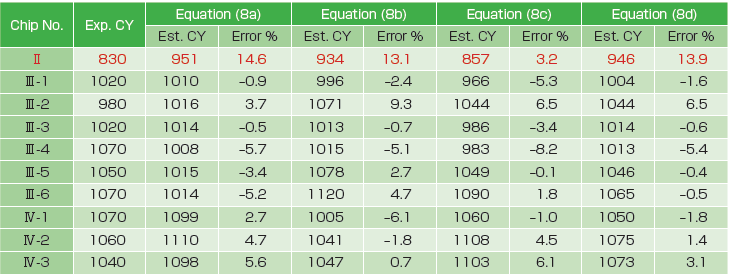
式(8)の疲労寿命評価式で予測した温度サイクル条件下の各チップの疲労寿命を表4に示します。これによると、チップII以外のチップについては予測結果と試験結果には良好な一致が見られました。チップIIの予測精度が低いのは、前述したようにチップIIの場合はE12でなくE45はんだ接合界面端近傍からき裂が開始することによるからです。また、疲労寿命評価式は試験結果を増やし定数の特異場パラメータ依存性を減らすことにより精度を上げることができます。式(8)の四つの疲労寿命評価式はいずれも疲労寿命を予測することができますが、試験結果数が少ないので、どの式が一番よいか判断が難しいところです。クリープ疲労破壊の特性から考えると、式(8a)のひずみ支配型疲労則と式(8d)の累積型疲労則がより適切であろうと推測されます。
温度サイクル試験に基づいて作成した疲労寿命評価式はパワーサイクル試験時の疲労寿命評価にも使うことができます。ただし、前述したように疲労寿命予測式の左辺の指数は材料定数で不変ですが、パワーサイクル試験と温度サイクル試験の応力繰り返し比等が異なるため、疲労寿命予測式の右辺の定数は変化します。パワーサイクル試験結果と対応する特異場パラメータを用いて作成したパワーサイクル試験時の疲労寿命評価式は式(9)で与えられます。また、この疲労寿命評価式で予測したパワーサイクル試験での各チップの疲労寿命は表5に示します。これによると、式(9)の疲労寿命評価式は試験結果をよく表現でき、とくに、式(9a)ひずみ支配疲労則と式(9d)の累積型疲労則が試験結果をよりよく表現できることが読み取れます。
ひずみ支配型疲労則

応力支配型疲労則
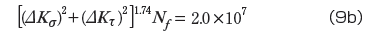
加速型疲労則
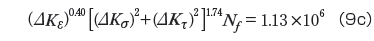
累積型疲労則
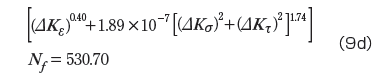
おわりに
本報では、はんだ接合界面端近傍の応力特異場パラメータについて、全体解析モデルとズーミング法を用いた部分解析モデルによる二段階解析法を提案しました。また、応力特異場パラメータに基づいて、はんだ接合界面端近傍の疲労則を構築しました。パワーモジュールを対象に温度サイクル試験条件下の特異場パラメータと試験結果を用いて作成したはんだ接合部の疲労寿命評価式は、試験結果をよく表現できたことから、提案した特異場パラメータの解析手法と構築した疲労則が妥当であることを明らかにしました。
所定形状のはんだ接合部の疲労則は材料特性だけに依存します。形状が相似で材料が同じはんだ接合部の熱疲労寿命評価には同じ疲労則の適用が可能です。
一方、はんだ接合界面端近傍の特異場パラメータの計算が複雑で、設計に使うには簡易に特異場パラメータを計算できるデータベースの構築が必要です。また、ニューロネットワーク等手法を用いて更なる試験結果、とくに、例えば異なる繰り返し加載条件下での試験結果の蓄積等により疲労寿命評価式を進化させ、その予測精度を向上させることが期待できます。
2.劉継紅,鉛フリーはんだSn96.5Ag3Cu0.5の材料モデリング,日本機械学会関西支部第84期定時総会講演会(2009.3)。
3.J. H. Liu, X. Q. Meng, J. Q. Xu, Creep Constitutive Relationships and Cyclic Behaviors of Sn96.5Ag3Cu0.5 under High Temperatures, Engineering Plasticity and its Applications, Proceedings of the 9th AEPA 2008, Daejeon Korea, pp.67-72. (2008.10).
(CAEのあるものづくり2012年16号掲載)
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

実測 × 解析で基板の熱変形問題を解決!基板反り現象の高精度シミュレーション
~エスペック(株)×サイバネットシステム(株)の連携ソリューション~
-

【全記事】CAEのあるものづくり vol.42
ユーザー様インタビュー記事7件を1冊に集約した保存版
-

誤差との上手なつきあい方 ~流体解析の計算誤差~ (完全保存版)
誤差との上手なつきあい方 前編・後編 を1冊にまとめた保存版 PDF
-

非線形解析の最大強度評価はAnsys LS-DYNAで解決!
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析で電子機器の信頼性向上
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

共振回避だけで終わらせない振動解析の進め方を解説(周波数応答・時刻歴まで)
~Ansys Mechanicalで実現する高度な製品開発~