みんなの公差
#16 3σ (シグマ) のルール
各シグマの意味を知り、シグマレベルごとの確率・不良率を表にまとめてみよう
今回は「3σ(シグマ) のルール」について、解説していきます。
前回の「正規分布と正規分布の確率」では「標準化」というお話をしました。部品によってばらつきや標準偏差の大きさがありますが、それを標準化することで、ひとつの尺度で確率を求めることができるという内容でしたね。
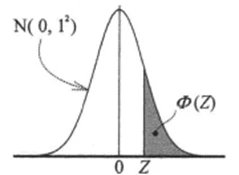
さて、ここに「Φ(1.00)」「Φ(2.00)」「Φ(3.00)」という3つの値がありますが、これらの意味をすぐに思い出せるでしょうか。
正規分布の確率
正規分布表の右下の図をご覧いただくとわかるように、正規分布におけるこの部分の面積、つまり確率を表しています。

標準化
以下の数値を正規分布表からみとることができます (正規分布表はこちら)。
- Z=1.00 のとき:Φ(1.00)=0.15866(約15.9%)
- Z=2.00 のとき:Φ(2.00)=0.02275(約2.3%)
- Z=3.00 のとき:Φ(3.00)=0.00135(約0.13%)
シグマに関わらず、1つの尺度で確率を求めることができます。
各シグマの意味とは
1σの確率
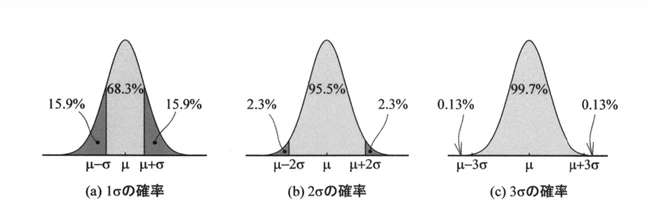
これは、正規分布における±1σの範囲を意味します。平均 (μ) は0で、標準偏差は1。片側の確率が15.9%であるため、両側で31.8%。それを100%からこの値を引くと、68.3%となり、適合する確率が 68.3 %ということになります。ものづくりの世界でこのような数値を使うことはほとんどなく、多くは 3σを使いますが、統計の基本ということで少々お付き合いください。
2σの確率
2σでは、片側が2.3%、両側で4.6%。つまり、100-4.6 = 95.4% が適合ということになります。
3σの確率
3σになると、片側が0.13%、両側で0.26%。つまり、99.7%の確率で適合することなります。不良率はわずか0.3%(千個に3個)。これが「3σのルール」といって、ものづくりのひとつの尺度になっている数字です。
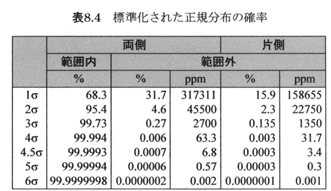
標準化された正規分布の確率を表で整理して理解しよう
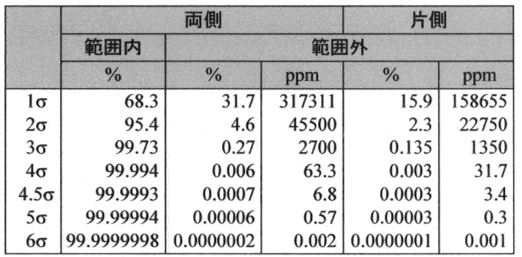
両側と片側の値が入り混じってくると、「どちらの話をしているのか分からなくなる」ことがよくあります。そこで、1つの表にまとめておくと、頭の中を整理しやすくなるのではないかと思います。
シグマごとの確率を確認する
標準化された正規分布の確率
まず、1σから見ていきましょう。片側で範囲外となる確率は 15.9%です。次に、2σでは2.3%。3σでは 0.135%です。このように、シグマが大きくなるにつれて確率の値はどんどん小さくなっていくことが分かります。片側の数値ですが、両側の範囲外確率は単純に片側の数値の2倍で計算されます。
3σ以降は確率が非常に小さくなっていくため、パーセント表記では扱いづらくなります。そこで、ppm(parts per million) を使うことがあります。
ppmとは
ppmは「100万分のいくつか」を表す単位です。パーセント(%)に比べて4桁分解像度が上がるため、小さな値でも比較的読みやすくなります。
σに対する正規分布の確率をグラフ化
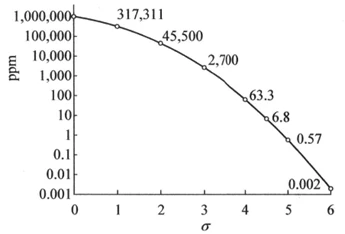
シグマ (σ) に対する正規分布の確率
このグラフはこの数値をプロットしたもので、縦軸が対数スケールになっています。このようにすると、確率の変化が直感的に把握できるカーブとなることが分かります。3σは一見非常に小さい値のように思えますが、ppmで表すと約2700ppm。4σ、5σと進むにつれて、その確率はさらに小さくなっていきます。
Q: ここでの 6σ は、CETOL 6σの「6σ」や 6σデザインとよく言われるものと同じもの?
6σ とは
「6σ」という言葉は、しばしば「プラス3σ、マイナス3σの合計=6σ」というように解釈されがちですが、正確にはそうではありません。6σとは、平均(μ)がシフトすることを想定したものです。
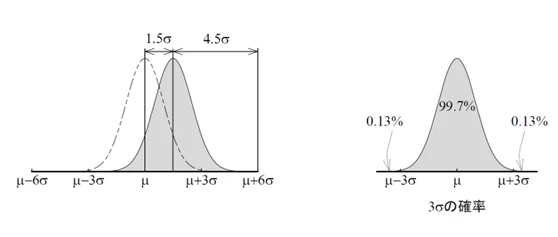
この図では、二点鎖線は平均値(μ)がずれていない状態を示しています。それに対し、平均値が1.5σ分右側(=上側)にシフトした状態を想定した場合のシナリオを示しています。もちろん、平均が左側(=下側)にずれるケースも考えられます。
つまり、工程の平均が多少ズレてしまったとしても、そこから4.5σの余裕があるという設計がなされているのです。
なぜ1.5σのシフトを見込むのか
標準化された正規分布の確率
現実には、製造された製品の特性値が常に目標値のど真ん中に来るとは限りません。そのため、工程平均が最大で1.5σ程度ずれることを想定し、そのズレを含めた上で規格を決めるというのが6σの思想です。
これにより、製品のばらつきに対する許容範囲が3σ(±3σ)から4.5σ(±4.5σ)へと広がり、結果として製品の不良率は飛躍的に低下します。
不良率と確率の関係
Cpkとの関係
Cpk(工程能力指数)は次の式で表されます。
Cpk = (USL - μ) / (3σ)
ここでUSLは上限規格値、μは工程平均、σは標準偏差です。6σでは、平均μが1.5σシフトしているにもかかわらず、上限規格値まで4.5σの余裕があるため、Cpkは: Cpk = 4.5σ / 3σ = 1.5 となります。Cpkが1.5という値は、一般的な業界基準と比べて非常に高い品質を意味します。
とはいえ、すべての業界においてこの6σ基準を一律に適用する必要はありません。製造ロット数や製品の使用目的、要求される品質レベルは産業ごとに異なるため、それぞれの企業が自社のノウハウや技術に基づいて、妥当な品質基準を設定することが求められます。
参考文献のご紹介
この6σの考え方に関する詳細は、複数の文献で解説されています。一部は無料で閲覧可能なものもありますので、6σの基本概念を学ぶ際には、ぜひ目を通してみてください。
- Mikel J. Harry, J. Ronald Lawson:
Six Sigma Producibility Analysis and Process Characterization
Motorola University Press, 1992. - D.H. Stamatis:
SIX SIGMA AND BEYOND Design for Six Sigma Volume VI Design for Six Sigma
ST. LUCIE PRESS, 2003.
https://doi.org/10.1201/9781420000290 (PREVIEW PDFあり 2025/5現在)
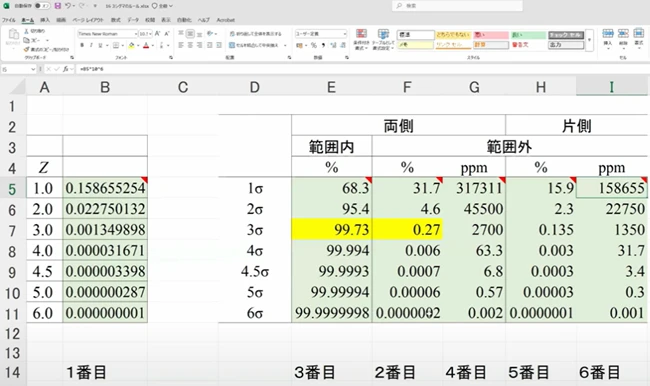
【演習】Excelで「3σのルール」表を作ってみよう
ここでは、実際にExcelを使って「シグマレベルごとの確率・不良率」を表にまとめていきます。画像のような表を完成させることを目標に、手順を1つひとつ説明していきます。
配布されているExcelファイルには、数式付きのメモが添付されています。そのメモをコピー&ペーストして使用しましょう。
3σのルールを動画で解説!
本記事の内容や Excel での操作を動画で解説しています。是非ご覧ください。