みんなの公差
#23 がた (後編)
2つ穴・長穴(長円の穴)のがたをアプリと計算式を使って解説
前編では、紙の上で断面を横から見るようなイメージで、一次元の「がた」について解説しました。また、LMVSやLMVCといった少し混同しやすい点があったため、その整理も行いました。詳細は「がた(前編)」の内容をご確認ください。
後編は、2つ穴の“がた”の話の締めくくりとして、その発展形ともいえる内容に触れながら、「穴」と「長穴」における“がた”について、もう少し詳しく解説していきたいと思います。
2つ穴のがた:アプリで「がた領域」と大きさを視覚的に確認
がたが土星の輪のような軌跡になる理由(がた領域の見え方)
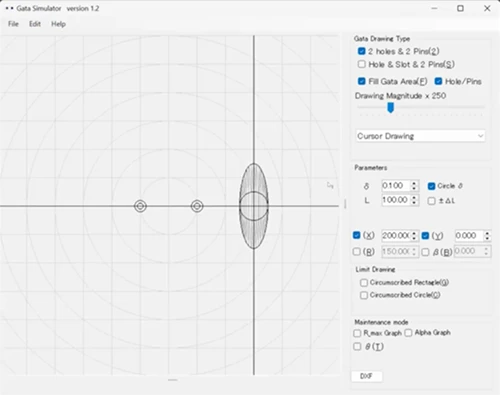
アプリで見る2つ穴のがた
それでは、アプリの画面を見ていきましょう。
ここには穴とピンの組み合わせが2か所あり、これを「2つ穴のがた」と呼んでいます。
設計では、このピンとピンの間に部品を配置したいところですが、事情によっては、どうしても張り出した位置に部品を配置しなければならない場合があります。こうしたとき、“がた”の影響がとても大きな問題になります。
このアプリでは、その“がた”がどのくらいの大きさになるのかを視覚的に確認できるようにしています。
スライダーを動かし続けると、軌跡がまるで土星の輪のような形になります。これは、実際にアプリを使う中で「こういう図形になるのか」と分かってきた点です。中心から離れていくほど“がた”は大きくなりますが、そのときは形だけでなく、大きさも知りたくなるはずです。アプリの挙動は是非動画にてご確認ください。
がたの大きさの求め方:外接する矩形・外接円で見積もる
大きさを求めるのは少し大変ですが、実は計算式があります。その式を使えば、図形にぴったり接する矩形を描いたり、円を描いたりすることができます。実務では、この「どれくらいの大きさになるのか」を知りたい場面が多いと思いますので、その計算式を提案しました。
もし式を使うのが面倒であれば、このアプリだけでも十分役立つと思います。また皆さんの中には、sin (サイン)・cos (コサイン) で計算したり、3D/2D CAD上で動かしながら“がた”の大きさを見積もったりしている方も多いでしょう。そういった方法と比べていただくと、ほぼ同じ結果になるはずです。実際、このアプリもCADでの動作確認と幾何学計算を重ねながら作っていますので、基本的には一致するようになっています。
ピン間距離Lを変えるとがたはどう変化する?(横方向/縦方向の違い)
2つのピン(あるいは穴)の間隔を変えると、“がた”は小さくなるのでは?と思ったことがありました。昔から何となくそう感じてはいたのですが、特に検証したわけではありません。ただ、「ピン間の距離を詰めると、何か良い効果があるのでは」と考えていたのです。
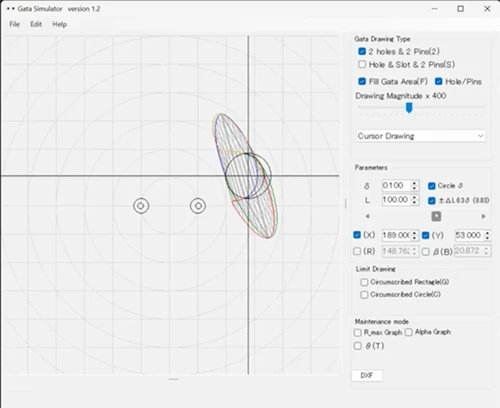
形や大きさの変化をアプリで確認
そこで、この“がた”の形を少し拡大して、「距離を変えると、形や大きさはどう変化するのだろう?」と考えてみました。その結果を、このアプリに反映したところ、画像のような変化をすることが確認できました。
たとえば、ピンを外側へ広げていくと、“がた”は確かに小さくなっていきます。特に左右方向(横方向)の“がた”は大きく減りますが、上下方向(縦方向)はあまり変わらないため、「思ったほど全体としては減らない」という印象になります。つまり、横方向の隙間は小さくなる一方、縦方向はほぼそのままなのです。
この機能は現在,森北出版にアップロードされているバージョンには実装されていません。
このように、がたの領域は徐々に小さくなっていきます。
なお、もし部品が回転しないと仮定すれば、中央の円形の領域が“平行移動のがた”になります。しかし、実際には部品が回転するため、領域は円ではなく、楕円のような形になります。ピン間の距離を変えると、この中央の円形だった部分が「猫の目」のようにだんだん細く縮んでいきます。これは、ピン間が詰まることで、円のように自由に動けなくなるためです。
このように、“がた”の形と大きさが、ピン間距離によってどのように変化するのか、アプリを使えば視覚的に理解できます。
ピン間隔とがたの関係(横は減る/縦は変わりにくい)
ここまでの内容を整理すると、次の通りです。
- 左右方向のがたは大きく減る(隙間が詰まるため)
- 上下方向のがたはあまり減らない(距離を変えても効きにくい)
- 最後まで詰めると、がたはゼロになる(ただし干渉の一歩手前)
- 実務では、詰め過ぎると組立干渉のリスクがある
- ピンを使ってがたを減らしたり、変形で調整する際には有効な場合がある
また、ピンを内側に寄せた場合も基本的には同じで、左右方向のがたはよく減る一方、上下方向はあまり減らないという結果になります。最終的に組み立てが難しくなるほどギリギリまで寄せると、上下方向のがたも減ってきますが、そこまでいくと今度は干渉リスクが高くなるため、実務では使いにくい印象です。
ただし、ピンを使ってがたをコントロールする、あるいはピンの変形を利用して微調整するような場面では、こうした特性を理解しておくことで、有効に活用できる可能性があります。
穴と長穴(長円の穴)のがた:なぜ丸穴+長穴で位置決めするのか
丸穴+長穴の位置決めが使われる理由(組み立て性・ばらつき対策)
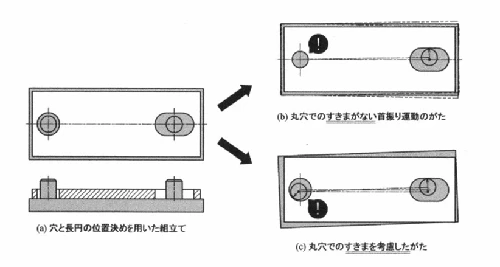
「丸穴」と「長穴」を組み合わせて位置決めしている例
先ほどは両方とも丸穴の例でしたが、ここではあえて片方を長穴にしています。その理由は、組み立て性を良くするためです。
もし、ピン同士の間隔にばらつきがあったり、部品側の穴の間隔にばらつきがあったりすると、両方が丸穴の場合は組み立てが難しくなる可能性があります。
そこで、一方を長穴にしてわざと余裕(すき間)を持たせることで、多少のばらつきがあってもスムーズに組み立てられるようにしています。
そのため、この方法はモールド部品やプレス部品でよく使われている一般的な設計手法です。
よくある誤解:支点で首振りするだけではない(平行移動+回転が混在)
この「丸穴+長穴」の位置決めは、現場でもよく使われる方法ですが、
「丸穴側を支点にして、首を振るようながたが出る」と説明されることがあります。
もし丸穴側が圧入されていて、がたがまったく無い状態であれば、その説明でも問題ありません。
しかし、実際の組み立てではすき間が生じることが多い です。
たとえば 0.02〜0.03mm 程度の隙間はどうしても生じます。その結果、
- 丸穴側でもわずかに平行移動が起きる
- 長穴側では回転方向の動きも起きる
といった複数の動きが同時に重なります。
つまり実際には、単純な首振り運動だけでは説明しきれないのです。
私自身も「実際どう動いているのか?」と長年悩んでいました。そこで、この“がた”の挙動をはっきりさせるため、数式や図形で整理して研究してきた、という背景があります。
穴+長穴のがた領域の特徴:2つ穴と似ているが少し広い
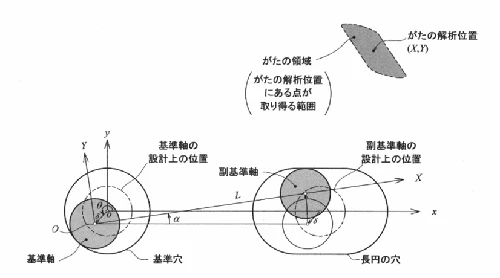
穴と長円の穴のがたの解析
丸穴が 2つの場合とよく似ていますが、丸穴と長円の穴の組み合わせでは、がたの形は少しだけ大きくなります。 片側のピンが任意方向に動くと、反対側のピンも上下方向に動くような連動した動きをするため、その動きをすべて重ね合わせることで、特定の点が描く「がたの領域」を求めることができます。
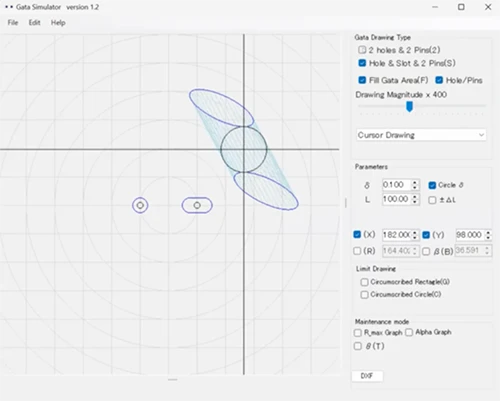
丸穴+長円の穴をアプリで確認
アプリで確認すると、丸穴が2つの場合は楕円に近い形になりますが、丸穴+長円の穴の場合も非常によく似た形となり、重ねて比べると、わずかに広いことがわかります。
長穴側の形が平行四辺形っぽくなる理由(上下方向の拘束)
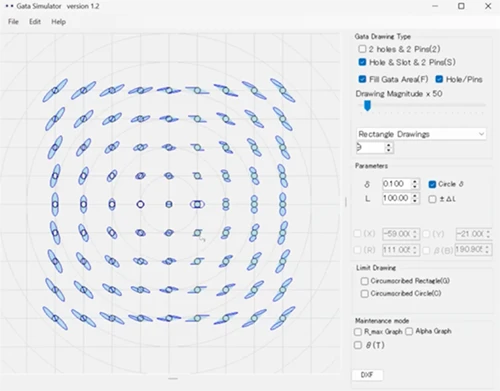
「丸穴+長円の穴」で位置決めしたがたの広がり
この図は、「丸穴+長円の穴」で位置決めした場合の“がた”の広がり方を示しています。
丸穴と長円の穴の近くでは動きは小さいですが、距離が離れるほど徐々に広がっていくことが分かります。
特徴的なのは、長円の穴側の周辺で、がたの形が一部「真四角(拡大すると平行四辺形)」のようになる点です。これは、長円の穴によって上下方向の動きが平行な面で拘束されているためで、その結果として、このような直線的なエッジを持つ形状が現れます。
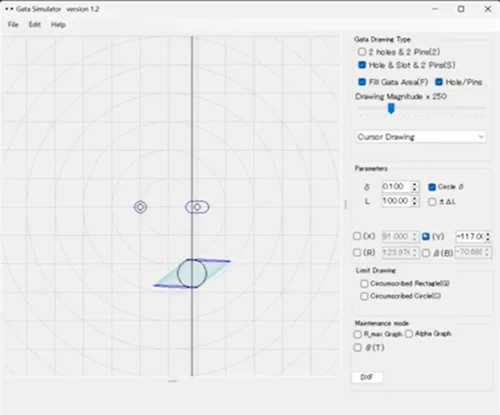
長円の穴の場合は平行四辺形のように
つまり、“丸穴2つよりも少し広がる” かつ
“一部が平行四辺形のような形になる” というのが、
長円の穴を使った場合のがたの特徴です。
穴+長穴のがたを計算
外接する矩形と外接円の式
前編で紹介した二つ穴の外接する矩形の式と比べると、穴と長円の穴の場合も考え方はほとんど同じです。実際に解いてみると、式の形としては大部分が共通しており、違いが出るのは主にX方向の成分だけでした。一方でY方向は結局同じになり、もともとがた領域の図形が二つ穴の場合とよく似ていることを考えると、納得できる結果だと言えます。
x方向の限界(外接矩形)
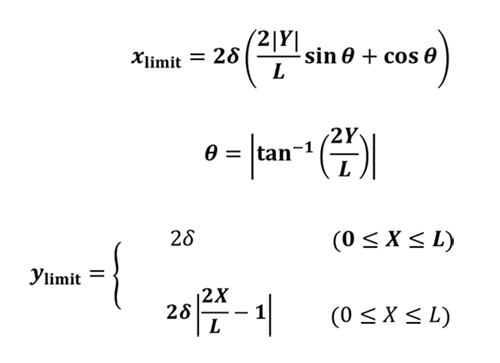
穴と長円の穴のがたの式1(外接する矩形)
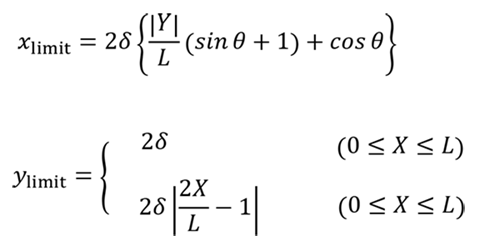
穴と長円の穴のがたの式2(外接円)
二つ穴の外接円のときも場合分けが必要で式が複雑でしたが、穴と長円の穴の外接円はさらに大変でした。式としてはここに示したように一見そこまでひどくないように見えますが、問題は角度 θをどう決めるかです。θ は部品が並進する方向、つまり並進のがたの向きを表す角度であり、この方向で外接円が最大になる条件を求める必要があります。その条件を整理していくと、最終的に sinθについての四次方程式にならざるを得ず、ここが計算上の難所になります。
外接円の直径
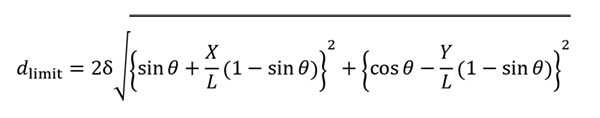
θを決定する条件
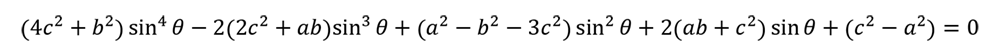
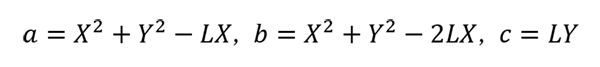
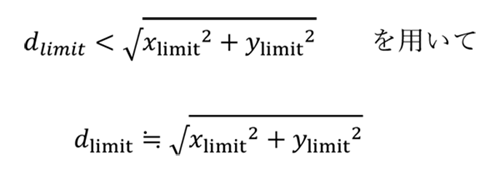
穴と長円の穴のがたをアプリで確認
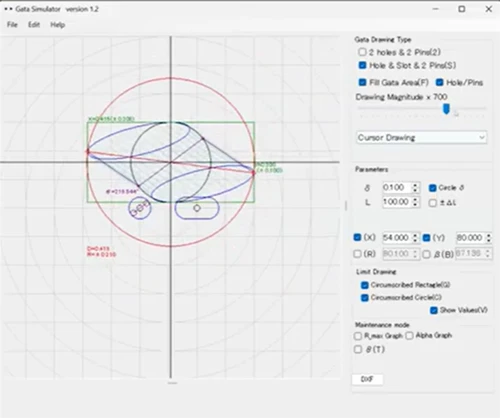
穴と長円の穴のがたをアプリで確認
アプリで確認すると、穴と長円の穴のがた領域にピタッと外接する矩形は、先ほどの式を使って計算できますし、同様に外接円も計算で求められます。
アプリの赤い円が外接円、緑の枠が外接する矩形です。ただ、外接円の計算は複雑なので、実務的には、矩形の角(緑の角)までの距離を求めた方が楽だということを示しています。必ずこの緑の角の方が、赤い円(外接円)の直径よりも外側に来ます。したがって、この角までの距離をニアリーイコール(近似値)として見積もっておけば、現実的には十分だと思います。
長円の穴の方がわずかに大きい理由とは
長穴なら動けるが、丸穴だと干渉して動けない領域がある
穴と長円の穴の型を比べてみると、形はかなり似ていますが、結果としては長円の穴の型の方が、がたがほんの少しだけ大きくなります。
これは、ピンが動ける範囲にわずかな違いがあるためです。
二つ穴(丸穴どうし)の場合、ピンは丸穴の円周に沿って動くため、動ける範囲は常に丸い境界で制限されます。
一方で長円の穴の場合は、丸穴と違って一部が削られているので、ピンが動ける方向が少し増えます。
そのため、長円の穴の方がピンが動ける範囲がわずかに広くなり、その分だけがたも少し大きくなる、ということになります。
もう少し見方を変えて説明すると、「長円の穴なら動けるけれど、丸穴だと動けない場所がある」ということがポイントになります。
図のようにピンがある方向へ動こうとしたとき、長円の穴であれば、図に示した範囲まで動けます。
ところが、もしそれが長円の穴ではなく丸穴だった場合、図に薄く描かれている円周のところで干渉してしまい、それより先には進めません。
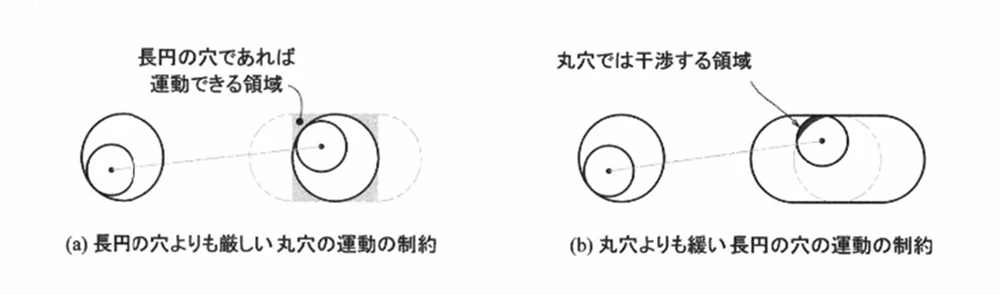
つまり、丸穴では届かない場所に、長円の穴なら届くようになるため、結果として穴と長円の穴の組み合わせの方が、二つ穴よりも動ける範囲が少し広がり、がたもわずかに大きくなるというわけです。
ただし、方向によってはこの違いがほとんど出ない場合もありますので、実務上は十分に使える位置決め方法だと考えられます。
例題で比較:位置決めレイアウトによるがたの違い
ここからは、3つの例題で位置決めレイアウトによるがたの違いを詳しく解説します。
詳細な解説内容は動画がわかりやすいため、
例題 1 : ピン間距離 Lを大きくすると、がたはどれだけ減るのか?
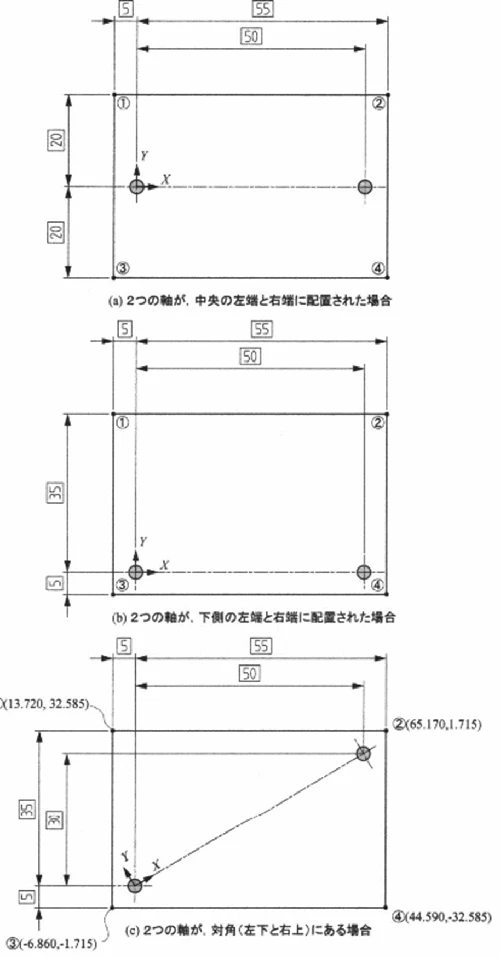
本例では、提案した計算式やアプリがX–Y座標で扱う形式になっているため、図のように紙(座標系)を斜めにして、ピンを結ぶ方向を基準とし、原点と座標軸を設定しています。このとき、四隅の点は斜め座標系での座標値がすでに与えられているため、式に代入するかアプリに入力すれば、各点のがたの大きさが求まります(距離の把握にはピタゴラスの定理の考え方が必要になります)。
この配置で四隅のがたを計算すると、結果は次の通りです。
①:0.311(ピンからやや離れているため、がたは大きめ)
②:0.248(ピンに近いため、がたは小さい)
③:0.248(②と同様にピンに近く、がたは小さい)
④:0.311(①と距離条件が同じなので、数値も同じに)
このように、ピンに近い位置ほどがたは小さく、遠い位置ほど大きくなるという基本傾向は変わりません。ただし今回のように Lを長く取ることで、以前の例で見てきた「0.4程度」の値や、四隅すべてが「0.371」だったケースと比べても、全体的にがたが減っていることが分かります。見た目の配置としては気持ち悪いと感じる人もいるかもしれませんが、がた低減という意味では機能的に優れた配置だと言えます。
例題2:横配置と縦配置で、張り出し先端のがたはどう変わるか?
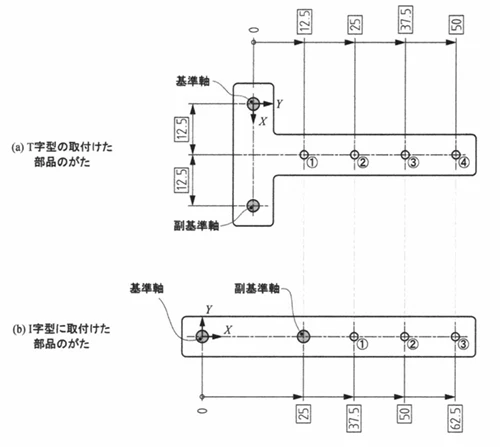
ここでは、位置決めが2点あり、その先端に何か部品を取り付けなければならない、いわゆる張り出し形状のケースを考えます。本当はこのような張り出し形状にしたくないのですが、実際の製品ではどうしても張り出さざるを得ないことがあり、そうしたところでは公差解析が必要になります。
今回比較したいのは、図に示すように、位置決めを横方向に並べたレイアウトと、縦方向に並べたレイアウトです。どちらもピン間距離 Lは同じで、条件は今までと同じにそろえています(ここでは L=25です)。つまり、純粋に「横に置くか、縦に置くか」で、先端側のがたがどのように変わるのかを比較します。
1点目:0.283
2点目:0.447
3点目:0.632
4点目:0.825
当然のことながら、位置決めから遠い点ほど、がたは大きくなります。
次に、位置決めを縦に配置した場合(先端が縦方向に伸びる配置)について同様に計算すると、結果は次の通りです。
1点目:0.400
2点目:0.600
3点目:0.800
このように、大きな差が出るわけではありませんが、今回の条件では縦配置の方がわずかにがたが小さいという結果になりました。イメージとしては「ここを中心に回るのだから、横でも縦でもあまり変わらないのでは」と思いがちですが、実際にはこのように数値として違いが出ることがあります。その点を示したくて、この例を取り上げました。
例題 3:穴と長円の穴の位置決めは「等価」ではない ― レイアウトでがたは大きく変わる
最後に今まで扱ってきた二つ穴(丸穴どうし)ではなく、穴と長円の穴の型で比較します。一般に、基準となる丸穴と丸ピンがあり、もう一方は副基準として、丸ピンと長円の穴で位置決めする構成がよく使われます。
今回比較したいのは、図(a)のように基準軸と副基準軸を両端に配置した場合と、図(b)のように基準軸を中央に置き、副基準軸を右端に配置した場合で、左右端(特に先端側)でのがたが同じになるのかどうかです。
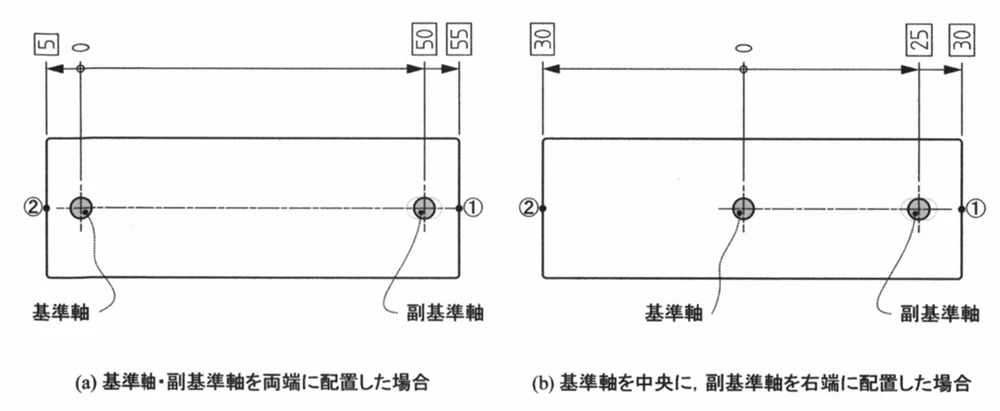
- 図(a)側(両端配置)のがた:0.298
- 図(b)側(中央+右端配置)のがた:0.240
- 図(a)側(有利な配置)のがた:0.316
- 図(b)側(不利な配置)のがた:0.680