みんなの公差
#22 がた (前編)
がたが公差解析で重要となる理由を、1次元・2次元の基本からわかりやすく解説
「みんなの公差」の中では、これまでさまざまな公差解析の話をしてきました。第21回までは「幾何公差・公差解析実践ハンドブック」の章立てのうち第8章として「統計」に関する内容を扱いました。公差解析を行う上で統計は避けて通れない要素であり、その必要性について説明しました。
また、統計の知識があまりなくても手っ取り早く実践できる公差解析の9章の部分も紹介し、それが公差解析の重要なポイントとなります。
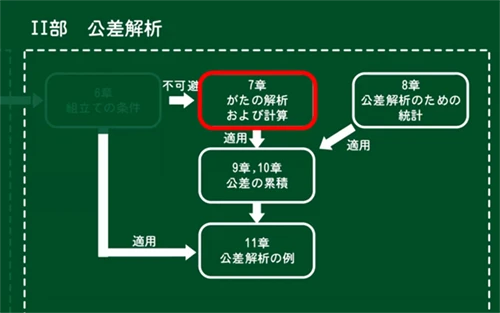
「幾何公差・公差解析実践ハンドブック」の章構成
そして、公差解析を進めていくと、避けては通れないのが「がた」です。「がた」は公差解析において組み立て部品の位置や動きを考える上で重要な要素です。今回からは「幾何公差・公差解析実践ハンドブック」の7章に含まれる、”がた”について解説します。
がたの基本的な考え方
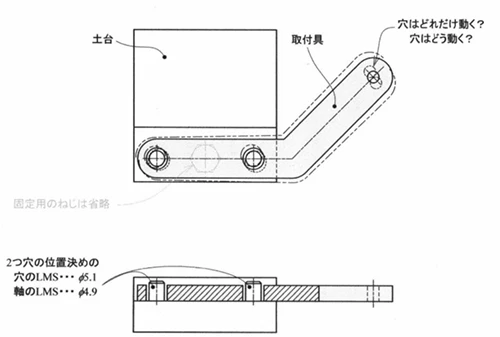
がたの例
まず、がたの基本的な考え方から説明します。多くの機械部品では組み立ての際にピンや穴を使います。たとえば、ブロックのような部品にピンで固定するブーメラン型の金具を取り付けるような構造を考えてみましょう。
真ん中をネジで固定し、先端部には穴が空いていて、そういったところにセンサーが取り付けられるとします。
このセンサーの位置が正確でないと、製品性能に悪影響を及ぼすことがあります。
取り付け時には、ピンと穴の間を、すきまばめで組み立てたいということが多いと思います。
しかし、この隙間ばめで取り付けると部品が微妙にずれてしまうことがあり、これを「がた」といいます。
がたが大きいと、センサーを取り付ける位置がずれてしまい、性能に影響を及ぼす可能性があります。
ここでは、がたを見込んで設計するための計算方法を紹介します。
1次元のがたと2次元のがたについて
一次元のがたとは
まず、シンプルな「1次元のがた」について考えましょう。最もシンプルな例として、板に開けた穴とピンで構成された構造を考えます。
2次元や3次元で考えると複雑になりますが、まずは平面上 (断面上) で考えていきます。
サイズ公差と幾何公差の関係
板に穴があり、別の板にピンが立っていて、それぞれにサイズ公差と幾何公差が与えられているとします。
ここで、サイズ公差と幾何公差の関係を見ていきます。
最小の場合の穴の直径が 5.1−0.1−0 = 5.0mm、軸の直径が4.9+0.1+0で5.0mmとなる場合、ギリギリで組み立てが可能です。
これを「実効サイズ」と呼びます。この状態では、部品同士がきつくはまり、ほとんど隙間がありません。
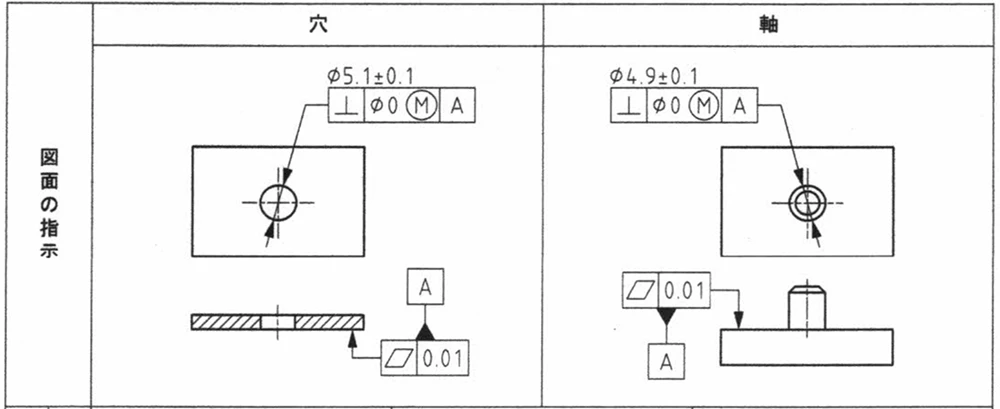
穴の直径が5.1+0.1で5.2mm、軸の直径が4.9−0.1で4.8mmになる可能性があります。つまり、穴と軸の差で0.4mmの隙間が生じます。
このときの隙間が最大がたであり、組み立てた部品が最も自由に動ける状態です。
このように、がたには「最小がた」と「最大がた」が存在し、設計段階ではどの状態を考慮するかを明確にする必要があります。
最大がたの状態を考えることで、最悪条件下でも製品が正しく機能するかを確認できるようになります。
最も緩い場合、これがいわゆる「ワーストケース」です。この状態を考慮しておく必要があります。
3つのがたの値
たとえば、穴の直径が5.1mmで、軸が4.9mmの場合、その中間に位置するのがノミナル状態です。
がたというのはどの状態で考えるかによって異なります。実際の公差解析では、どの状態を指しているのかを明確にするため、それぞれに名称がついています。この場合、最もがたが大きい状態を「最大のがたの値」と呼び、逆に最も小さい状態を「最小のがたの値」としています。この例では、最小のがたは0に設定されています。
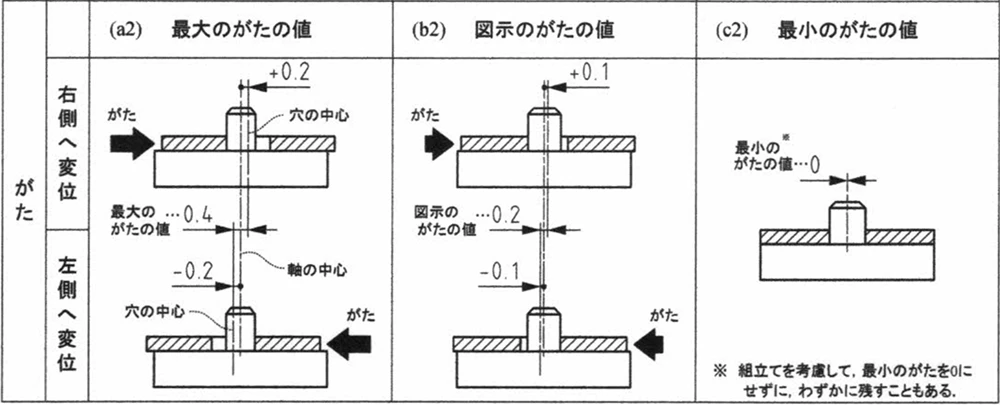
最大がたの値
図示のがたの値
最小のがたの値
設計時には、組み立てを考慮してごくわずかに隙間を設ける場合もあります。今回の例では、ぎりぎり組み立てが可能なように設定しているため、がたは0としていますが、実際の組み立てではわずかなすきまを持たせることもあります。
このように、がたには3つの代表的な状態があります。
公差解析では、ワーストケースとして最大がたの値を考えるのが一般的です。
さらに、これに統計的なばらつきを加味して解析することもあります。
がたと幾何偏差の関係
ここで、がたと幾何公差(位置や姿勢などの偏差)との関係を整理しておきましょう。
最小のがたが生じる状態は、MMVC(Maximum Material Virtual Condition)と呼ばれます。
これは、穴が最も小さく、軸が最も太い状態を指します。今回はこの状態を基準としてがたを0に設定しました。
このMMVCという言葉は、日本語では「最大実体実効状態」と訳され、やや分かりにくい用語です。
がたが最も大きく生じる状態は、幾何公差の考え方でいえば LMVC(Least Material Virtual Condition)に対応するようにも思えますが、ここで扱うがたの最大の状態はそれとは異なります。
最小のがたが生じる状態 … MMVC(Maximum Material Virtual Condition)
最大のがたが生じる状態 ≠ LMVC(Least Material Virtual Condition)
図で確認すると、MMVC とLMVCを混同しやすいのですが、Ⓜは軸が最大のサイズ、つまり最も太い状態を示します。
Ⓜ は穴の最小寸法ではなく、材料が最も多い状態(最大実態)を意味します。この違いを正しく理解しておくことが重要です。
ⓂとⓁの違い
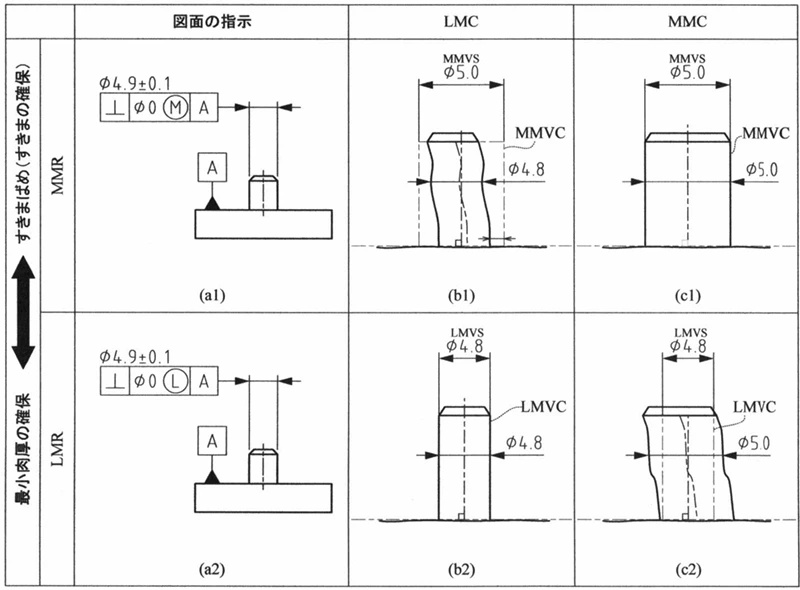
がたがいちばん大きい状態が Ⓛ かというと、そうではありません。Ⓛ は最小肉厚の確保を意味します。
つまり、軸がいちばん太い場合(4.9+0.1=5.0、MMC)で、外側から測った極部サイズが5.0だったとしても、4.8より内側に細らないことを保証するためのものが Ⓛ です。
もちろん、直径がいちばん小さい4.8の時は、これ以上内側に寄ってはいけないので、ピンはまっすぐ立てなければなりませんが、その範囲内でのばらつきは許容されます。
したがって、最小のがたが生じる状態というのは、LMVSやLMVCと呼ばれる「これ以上内側によって細らない(軸が細くならない)」領域の話とは別であることを理解していただきたいです。
プリントにも記載されていますが、Ⓜ は隙間確保を目的とした指示であり、Ⓛ は最小肉厚を確保するためのものです。
この点は混同しやすいので注意が必要です。
がたが最初に生じる場合はいわゆる Ⓜ (MMC) の状態であり、一方で最大のがたが生じるのは、直径が小さく(例:4.9±0.1 → 4.8 の場合)、かつ幾何偏差(ここでは直角度)が0のときです。この状態で最も隙間が大きくなります。
つまり、Ⓛ ではなく、特別な追加指示も存在しません。
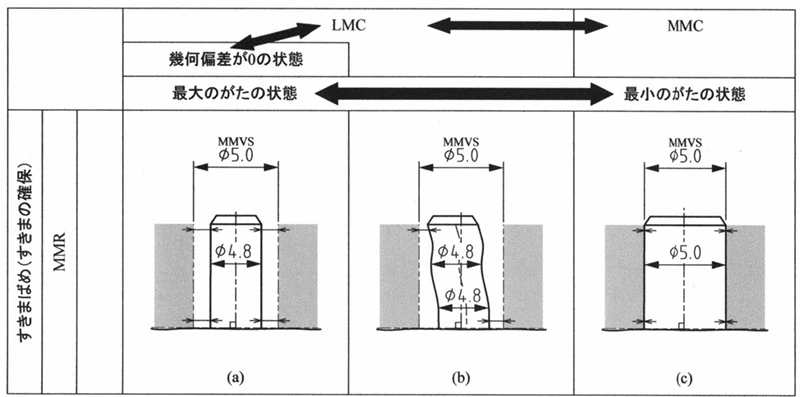
その中間状態では、軸が曲がっていたり、倒れていたりすれば、がたは減少します。
以上のように、がたと幾何偏差との関係を整理しました。
幾何公差の話は「みんなの公差」では触れていなかったため唐突に感じるかもしれませんが、設計工学会の動画も併せて見ていただくとMMVCの意味が理解しやすくなります。
2次元のがた
さて、次は2次元のがたの話に進みます。
2次元のがたには2つ穴のがたと、穴と長円の穴がたの2つがありますが、今回は2つ穴のがたの前半についてお話しします。
2次元がたの実例と課題
ここに2つの部品が組み合わされている例を示します。構造はシンプルで、板に2本のピンが立ち、板に2つの穴が開いています。
図では隙間を誇張していますが、実際にはここまで隙間は大きくはありません。
設計者としては狙ったど真ん中で組み立ててほしいところですが、組立作業者は限られた時間で作業するため、基本的には挿入してどこかをネジで止めることになるでしょう。
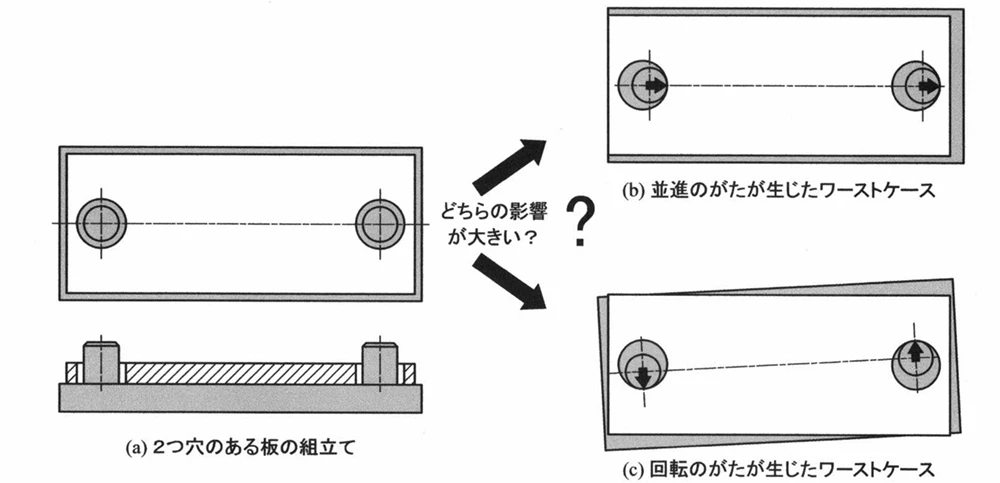
この大きさ(影響)を予測するのが設計者の仕事です。
この予測は私の昔の経験も含め、これは意外と難しいです。
上側の板が下に行くケースを考えると、単純に下がる場合もあれば、回転で角が大きく下がる場合もあります。
両方とも大きくなり得るし、どちらが大きいのか、その中間はどうか――こう考え始めると難しいのです。
公差解析では回転を考えることが多いのですが、並進と回転が混在するのが計算をやっかいにしているところだなと、私は感じています。
がたの定式化の研究
昔の話になりますが、CADで動かしてがたを求めるものの、どうにも腑に落ちない部分がありました。
そこで、教育・研究機関に勤めるようになってから,がたの計算の定式化を目指して研究してきました。
ここでは穴とピンだけに簡略化し、Lも非常に短くしています(動画では図を分かりやすくするために短くしていますが、通常はここまで短くしません)。
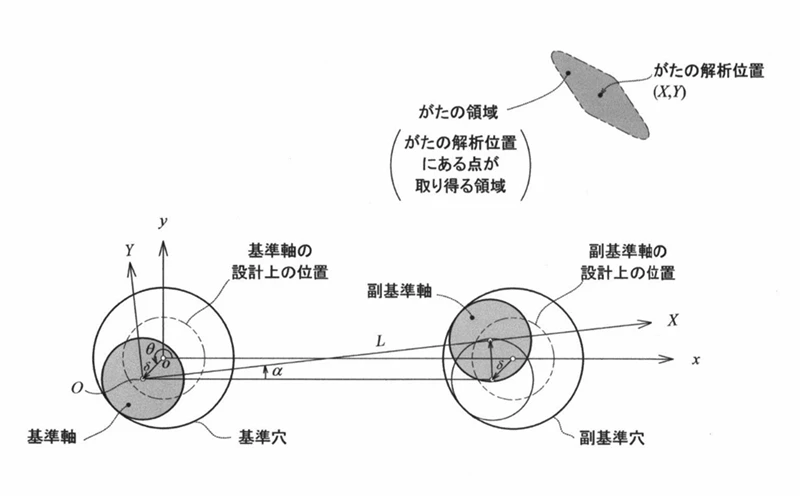
ポイントだけ伝えると、穴の中でピンが自由に動き、どこで組み立てられるかはわかりませんが、最初の例のようにセンサーの位置や部品間の隙間など、重要な箇所があります。
がた解析位置と領域の考え方
その領域がわかれば、並進が悪いのか、回転が悪いのか、あるいは両者の組合せが最悪なのかが見えてきます。
最終的に、その領域に内接(あるいは外接)する円の大きさがわかれば、がたの計算ができます。
2つ穴のがたの式 1 (外接する矩形)
2つ穴の場合のがたの式は次のとおりです。
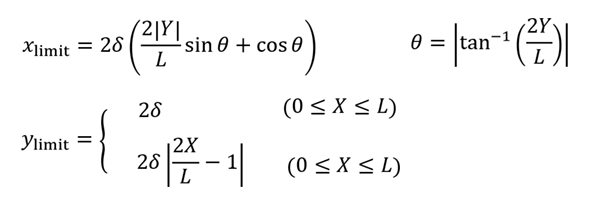
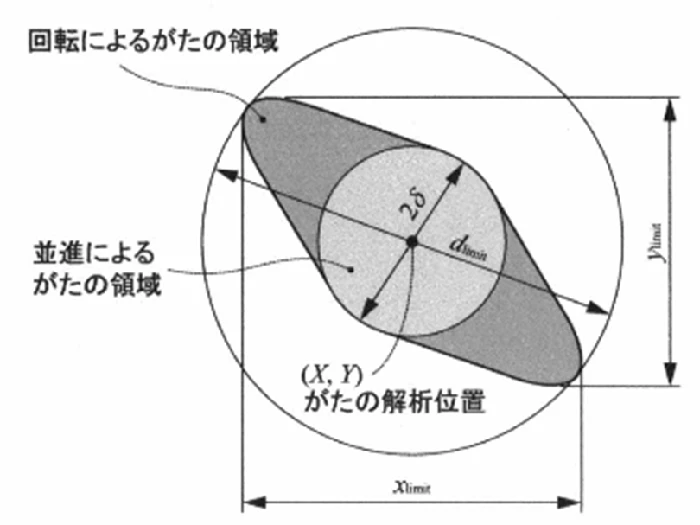
2つ穴のがたの領域の拡大図(外接する矩形および外接円)
回転がなければ解析点が描くのは円ですが、回転を含めるとレンズ状・ひし形状などの広がりを持つ領域になります。
そこで、領域の縦方向の大きさを y、横方向の幅を x(limit) と名付け、これらを求める式で領域を表現します。
見た目はやや複雑でも、考え方は比較的シンプルに収まります。
角度 θ の意味と求め方
解析では「どの方向へ並進したか」を角度 θ で表します(右=0°、上=90°、左=270°…)。
並進したあとで回転する、という組合せを考えますが、向きそのものは θ = arctan(2y / L)(L はピン間距離、y はがたの解析位置)にて求められ、そこまで難しくはありません。
2つ穴のがたの式 2 (外接円)
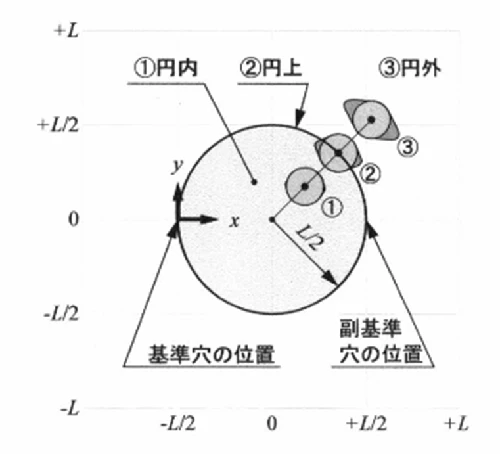
円の内側・円上・外側における解析点の場合分け
円の内側・円上・外側における解析点の場合分けは3通りあります。
穴とピンの相対位置に描いた基準円の円より内側・円上・外側に解析点が位置するかで場合分けをします。
分岐に応じて sin・cos の符号が入れ替わったり、分母が0になる特異ケースを特別扱いしたりしますが、場合分けを正しく行えば問題はありません。
円の直径 Dlimit についてはそれぞれの場合、下記のような式で求められます。
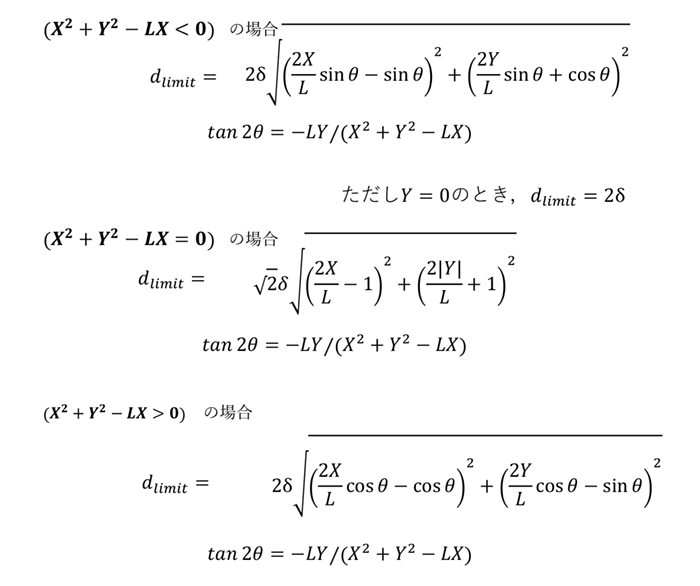
アプリで可視化:複雑な条件でもがた領域が一目瞭然
今までさまざまな式をみていただきましたが、実際にアプリに落とすと、2本のピン(ピン間距離 100 mm など任意設定)と任意の解析点(例:x=200, y=0)を与えるだけで、その点が取りうるがた領域が塗りつぶしで描けます。より複雑な条件でも同様で、解析点がピンに近いほどがたは小さく、離れるほど大きくなる、といった直感的な傾向も図として確認できます。直交座標でも極座標でも描け、遠方へ行くほどがたが大きくなる形状が視覚的に分かります。
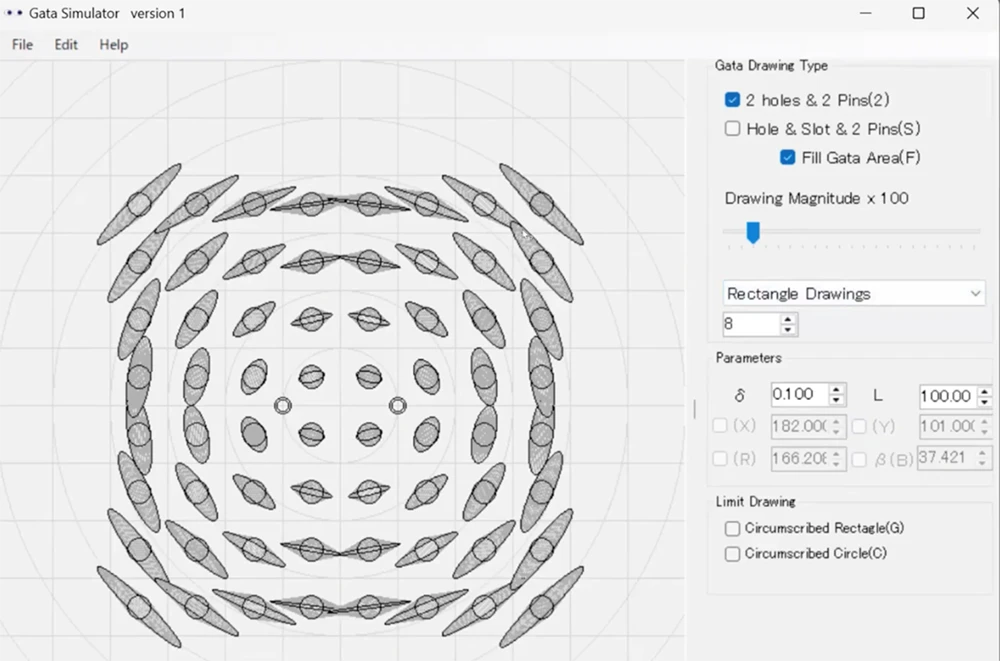
アプリで試してわかった知見
実験的に確かめると、ずっと動かしてもその成分が変わらない、という興味深い性質があります。
穴と長穴との比較
形状は非常によく似ていますが、よく見ると長穴の方がやや「はみ出す」感じで大きくなる傾向があります。
結果としては近い領域でも、がたが生じるメカニズムに違いがあり、その違いが形状わずかな差として現れます。
内接円・矩形の評価
内接円の厳密解はやや大変でしたが、式を整備して実装し、アプリで自動計算できるようにしました。
アプリと検証のすすめ
CAD上で座標を確認しながら本アプリの結果を照合すれば、直感と整式化の両面から理解が深まります。
これまでの成果は論文としてまとめていますので、理屈の裏付けや導出過程に興味のある方はぜひご参照ください。
参考文献
二つ穴の位置決め
- 2組の穴とボスとを用いた位置決めによる組立ばらつきの解析, 設計工学,54,7(2019)pp.457-472.
- 二組の穴とボスとを用いた位置決めによる組立ばらつきの解析
(第2報,がたの領域に外接する円の半径の導出), 設計工学,57,12(2022)pp.607-620. - 二組の穴とボスとを用いた位置決めによる組立ばらつきの解析
(第3報,ボス間の距離に偏差が生じた場合のがたの領域の変化), 設計工学,60,9(2025)pp.487-502.
穴と長円の穴の位置決め
- 穴と長円の穴を用いた位置決めによる組立ばらつきの解析, 設計工学,52,9 (2017)pp.553-556.
- 穴と長円の穴を用いた位置決めによる組立ばらつきの解析
(第2報,がたの領域に外接する円の半径の導出), 設計工学,60,1(2025)pp.27-38.
ダイアモンドピンの位置決め
がた (前編) の解説を動画でチェック
まとめ
本稿ではがたの定式化と可視化を通じて、2つ穴および長穴のがた領域、がたの領域に内接する円の直径、場合分け、そして興味深い不変性などの性質を示しました。アプリを用いれば、平行移動・回転を総合したワーストケースを、図として直感的かつ定量的に把握できます。出版社の許可が得られ次第アプリ公開を予定していますので、ぜひ触って確かめてみてください。