みんなの公差
#21 システムモーメント法
平均・標準偏差・ゆがみ・とがりから分布形状を予測する公差解析手法
公差解析ソフトを利用する際、「システムモーメント法」と「モンテカルロ法」のいずれを使うか、という二択になることがよくあります。ここでは、そのうちのシステムモーメント法について解説します。
システムモーメント法とは
システムモーメント法とは、公差解析に関わる各寸法の
- 平均 μ
- 標準偏差 σ(分散)
- ゆがみ γ1
- とがり β2
という 4 つのパラメーターから、出力として解析寸法の μ,σ,γ1 ,β2 を返す公差解析手法のことです。
たとえば 4 枚の板を単純に積み上げた場合でも、それぞれの板に平均が 0、標準偏差が一定の値、そしてゆがみやとがりの数値があると、全体として左に寄ったり、中央が尖ったりといった分布になります。ゆがみやとがり、標準偏差の値を少し変えることで、横に広がった分布になるなど、さまざまな形の分布が得られます。また、とがりの値を減らしていくと、半円分布に近い形になります。とがりが1.8程度になると、一様分布に近づきます。
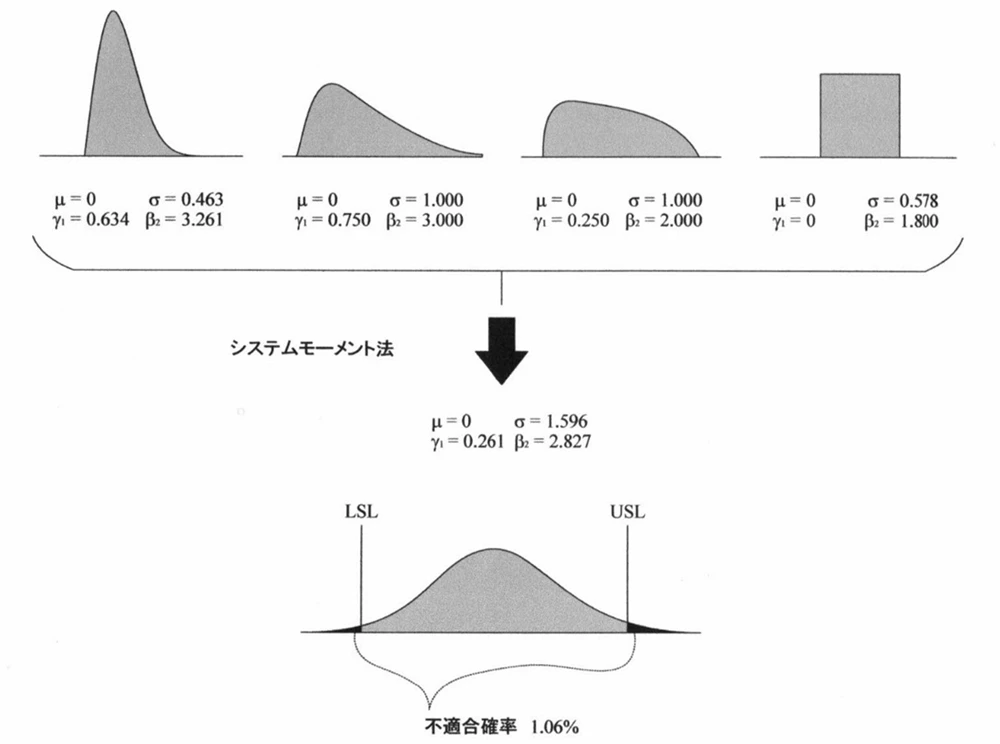
このように、4枚の板を積み重ねたときにその高さの分布がどうなるかを求めると、結果として平均(μ)、標準偏差(σ)、ゆがみ(γ1)、とがり(β2)という4つの数値が返ってきます。これが “システムモーメント法”です。つまり、入力としては「4つのパラメーター × 積み重ねの数」、出力としては「4つの統計量」が得られる、という仕組みになっています
システムモーメント法の計算の流れを簡単な例でご紹介
ここからは、JIS B 0625:2021「公差解析用語」附属書Dに記載されている「システムモーメント法の一連の流れ」を、よりわかりやすく簡略化して説明します。
これまでの例では、「10 ± 0.3 mm」のような単純な寸法公差を扱ってきました。今回は、この値が正規分布ではなく一様分布に従う場合、2枚の板の厚さがどうなるか?について例を見てみましょう。
【演習ファイルダウンロード可能】2枚の板の厚さがどうなるか? を計算してみよう
それでは実際に、Microsoft Excelを使ってモンテカルロ法の実験をしてみましょう。
動画を見ながら演習で使える2種類の Excel ファイル (演習用/記入結果)を下記よりダウンロードいただけます。
入力値は以下の2つです。
- 板A (x1) の厚さ:10 ± 0.3 mm
- 板B (x2)の厚さ:10 ± 0.3 mm
「標準偏差」「ゆがみ」「とがり」を計算
以前に「さまざまな確率分布」の回にて、さまざまな分布が存在するという話をしました。いくつかの分布を紹介した中で、一様分布というものがあります。
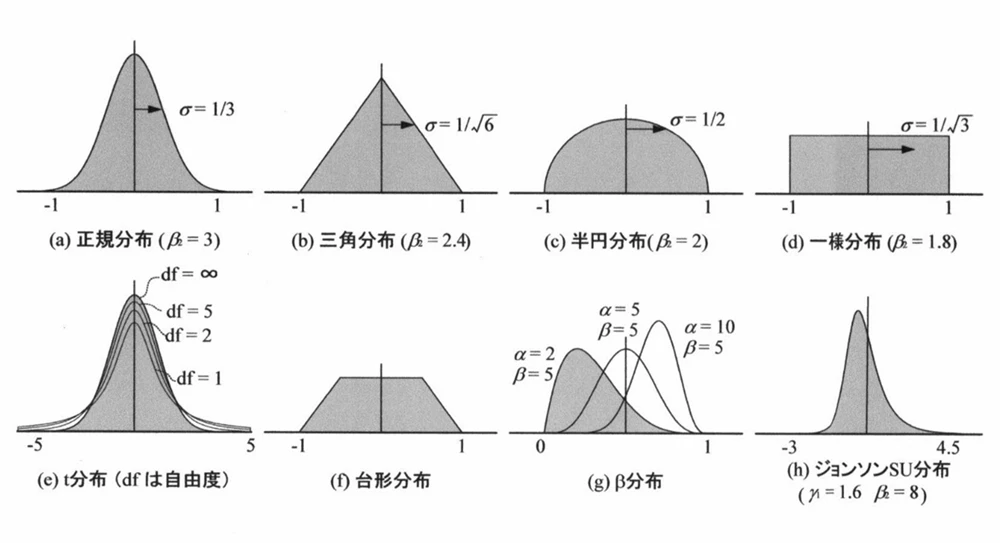
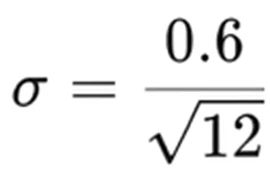
仮に範囲が±1であるとした場合、そのときの標準偏差は1÷√3となります。これを今回の例である±0.3に置き換えると、この0.6を√12で割った値が標準偏差となり、下記の式で求められます。
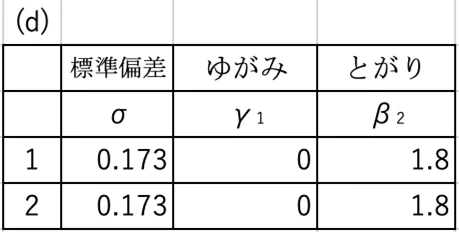
ゆがみに関しては0であり、とがりに関しては1.8です。先ほどの資料にも記載されている通り、とがりの値は1.8となります。ちなみに、正規分布では3、三角分布では2.4です。実際に現れる分布では、とがりはおそらくこの程度の値であることが多いと思われます。
偏微分係数 = 感度について
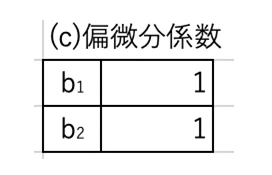
偏微分係数という項目が登場しますが、これはこれまで説明してきた「感度」と考えて差し支えありません。この例では板を単純に積み上げているだけですので、偏微分係数の値は1のままです。この係数が1であることは、後の計算を楽にします。
各寸法の平均値周りのモーメントについて
次に「各寸法の平均値まわりのモーメント」についてです。モーメントには1次から4次まであり、1次は平均値を求める際に用い、2次は分散や標準偏差の計算に使用します。3次はゆがみ、4次はとがりを計算する際に用います。平均値周り、原点周りのモーメントというものもありますが、少々複雑なので、また特別回ができたらその際にご説明できればと思います。
ここでは、標準偏差を二乗すれば分散となります。ゆがみについては0であるため、結果も0になります。隣にある分散の3/2乗という考え方は少し複雑ですが、ゆがみが3乗に関係することを思い出していただければ理解しやすいでしょう。これまで2乗、3乗、4乗といった流れをご紹介してきましたが、ゆがみは3乗となるため、その影響が関係していると考えてください。なお、ゆがみの値が0であるため、最終的な結果も0になります。2枚目の板についても同様です。
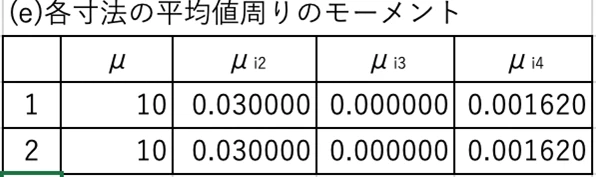
4次モーメントについては、今回はとがりを持つ分布であるため、とがりの値を掛け合わせて計算します。これはE7の項に相当します。このとき、分散を2乗し、さらにとがりを掛け合わせることでモーメントの値を得ます。数値としては非常に小さく、0.01や0.001620といった値が得られます。
uの平均値周りのモーメントではテイラー展開が必要に
次に「uの平均値周りのモーメント」についてですが、ここでいうuとは板の厚さ、すなわち解析寸法を指します。さらにこのuを“テイラー展開”して解析を行います。
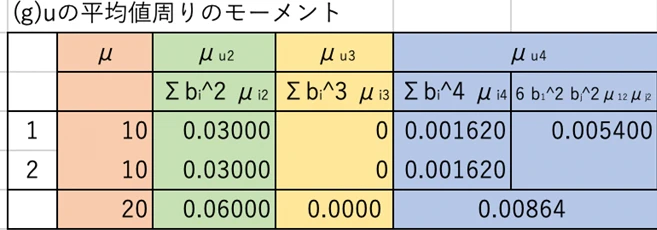
大学の数学で登場するテイラー展開は1変数の場合が多いですが、公差解析では扱う要素が複数となるため、多変数のテイラー展開が必要になります。要素数が増えるほど計算が複雑になるため、このあたりが非常に難解な部分です。私自身も理解に苦労した箇所ですが、このようにして多変数の関係を近似的に展開していくのが、システムモーメント法の特徴のひとつです。
システムモーメント法による考え方
求めたかったのは「とがり」の値
動画では『JIS B 0625:2021 公差解析用語 附属書D』の流れに沿って、各寸法の平均値周りのモーメントを計算し、それらを解析寸法 (μ) に対するテイラー展開で偏微分係数(β)(感度)と組み合わせて結果のモーメントを算出する手順を示しました。電気回路などでは分母や平方根に現れる非線形のためテイラー展開が必須となり、係数の2乗・4乗や公差項(例:6bi^2など)が登場して式が複雑化することがあります。
なお、σは分散の加法性から求まり、βは4次モーメントを標準偏差の4乗で割ることで最終的に「2.4」というとがりの値を導出できます。
結局のところ、今回求めたかったのは、この「とがり」の値”2.4”だけと言っても過言ではありません。分散については加法性の法則で求められるため、特に不自然な値ではありませんが、本当に知りたかったのはこの “とがりの値がいくつになるか” という点です。
「とがり=2.4」の意味するところは三角分布
さて、この「とがり=2.4」という値が何を意味するのかというと、これは三角分布を示しています。昔から、一様分布どうしを掛け合わせると三角分布になることはよく知られています。実際に計算をしてみると、複雑な式の結果として2.4という数値が得られます。
つまり、「結果として得られる分布は三角分布である」ということが分かった、というのが今回のポイントです。
3次元公差解析ツール CETOL 6σで検証
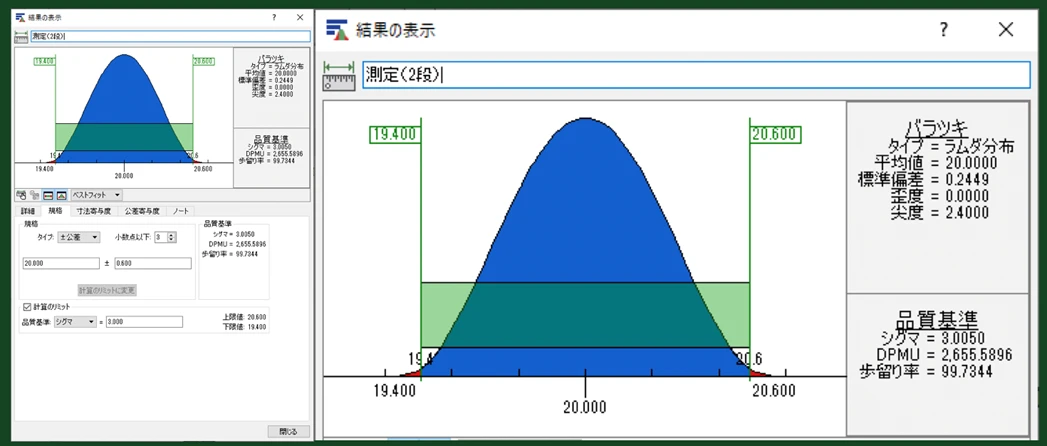
CETOLで見る分布の形状
CETOL 6σで確認してみると、実際の分布も下記の図のような形になっています。理想的な鋭い三角形にはならないものの、ほぼ三角分布に近い結果が得られます。これは、ラムダ分布などで分布を表現する際の限界によるものです。
応用例:2枚ではなく、さらに多く積み重ねた場合は?
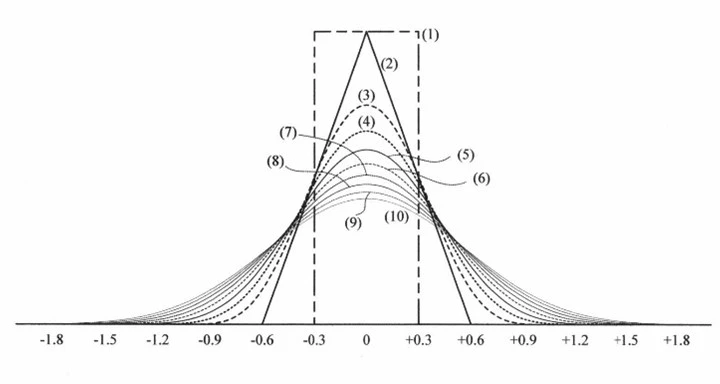
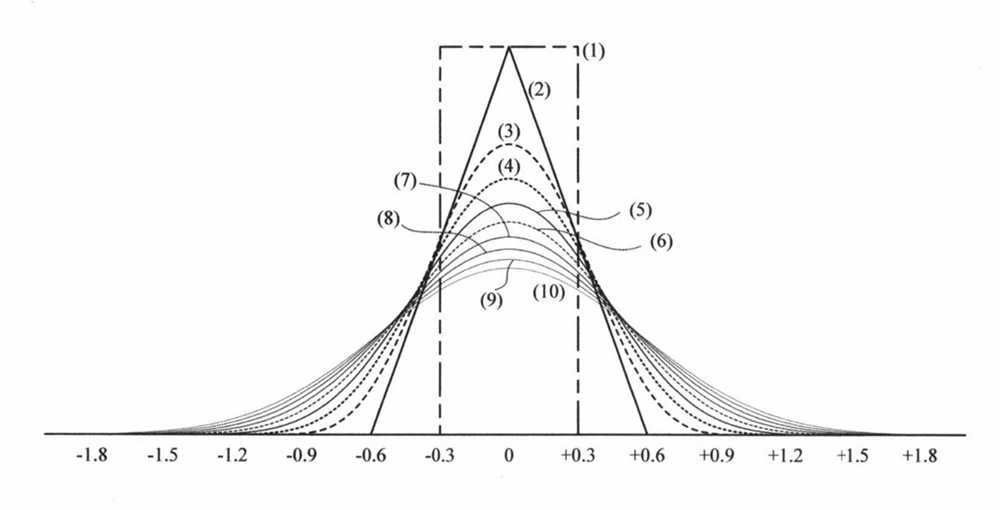
次に、この一様分布の板を2枚ではなく、さらに多く積み重ねた場合を考えてみましょう。1枚のときは一様分布、2枚では三角分布になります。3枚になると分布の形が少し丸みを帯び、4枚、5枚、6枚と増やしていくにつれて、より滑らかで平らな分布になっていきます。最終的には、正規分布に非常に近い形になることがわかります。
「とがり(尖度)」を数値で確認
また、「とがり(尖度)」の値を数値で見てみると、一様分布では1.8、正規分布では3.0という値を取ります。積み重ねる板の数を増やしていくと、とがりの値は1.8から徐々に3.0に近づいていきます。およそ10枚程度積み上げると、ほぼ正規分布に近い分布形状になることが確認できます。
まとめ
このように、システムモーメント法を用いることで、平均・標準偏差・ゆがみ・とがりの4つのパラメーターをそれぞれ入力すれば、結果として得られる分布の4つのパラメーターを求めることができます。その結果から、たとえば製品の組み立てにおいて「この範囲が合格、これを超えると不合格」といった適合率を計算することが可能になります。つまり、この手法を使えば、公差解析を行うことができるのです。
今回の解説では、あまり深い部分までは踏み込みませんでしたが、さらに奥まで理解しようとすると、式の変形をひたすら繰り返すような、かなり複雑な内容になります。 正直なところ、機械系の分野で大学時代に学んだ数学だけでは、完全に対応しきれないと感じる部分も多いです。私自身も試行錯誤しながら問題を解き、さまざまな方にご指導をいただく中で、ようやく少しずつ理解がつながってきたところです。
今後、もし機会があれば特別回を設けて、このシステムモーメント法についてもう少し詳しくご説明できればと思っておりますのでご期待ください。それでは、今回のシステムモーメント法の解説はここまでとさせていただきます。