みんなの公差
#20 モンテカルロ法
公差解析においてもよく用いられる乱数を用いた数値計算
モンテカルロ法とは
モンテカルロ法とは、乱数を用いて数値計算を行う方法で、公差解析においてもよく用いられています。名前の由来は、あの有名なカジノで知られるモナコのモンテカルロに因んでいます。
これまで、正規分布の組み合わせについて扱ってきましたが、それは正規分布に「再生性」があるからです。つまり、正規分布同士を足し合わせても、結果はまた正規分布になるという性質があります。
また、「分散の加法性」も関係しています。分散は、それぞれの分散を足していくことができます。そのため、正規分布同士の組み合わせであれば、標準偏差を2乗して足し、それにルートを取るだけで、比較的簡単に全体のばらつきを求めることができます。
ところが、実際には正規分布でない分布(非正規分布)を持つ場合もあります。そうした場合に有効なのが、今回紹介するモンテカルロ法です。非正規分布同士の組み合わせを扱う際、最もシンプルでわかりやすい手法のひとつです。
なお、次回ご紹介する「システムモーメント法」も、こうした解析に使われますが、まずはモンテカルロ法を理解することが大切です。
「モンテカルロ法」と聞くと、名前だけは知っていても、専用の高価なソフトがなければ使えないのでは?と思われがちですが、実はMicrosoft Excelでも、ある程度の解析は可能です。ですので、今回はExcelを使ってモンテカルロ法を体験してみましょう。
モンテカルロ法の使いどころ
モンテカルロ法が役立つケースは、先ほどのように非正規分布がある場合だけではありません。もう一つ重要な活用場面があります。それは、「確率変数の積」が関わる場合です。
これまでの例は、板を積み上げたような「足し算」や、「穴と軸のはめあい」のような「引き算」でした。これらは分散の加法性が使えるので、比較的単純でした。
しかし、機械設計などの現場では、確率変数同士の積で特性が決まるケースもあります。たとえば、円筒容器の体積を考えてみましょう。
直径Dがばらつく確率変数で、Hは定数または別の変数とします。体積Vは、
V = ¼πDh
で表されます。この場合、DもHも変数であり、積の関係になります。このようなケースでは分散の加法性が使えません。したがって、こうした「積」を含む解析には、モンテカルロ法が非常に有効です。
さらに、少し複雑な例として、「ガタ(あそび)」の解析もあります。たとえば、穴と軸のはめあいで、隙間が確率分布に従っており、その隙間にさらにガタが発生する場合。このとき、ガタの計算は足し算ではなく積になることがあるのです。
このように、分散の加法性が使えない状況では、モンテカルロ法が大きな助けになります。
【演習ファイルダウンロード可能】Excel でモンテカルロ法の演習をしてみよう
それでは実際に、Microsoft Excelを使ってモンテカルロ法の実験をしてみましょう。
動画を見ながら演習で使える2種類の Excel ファイル (演習用/記入結果)を下記よりダウンロードいただけます。
今回は「2枚の板の積み上げ」を題材にします。すでに何度か扱ってきたとおり、10±0.3板を2枚重ねた場合、合計の厚さがどうなるかという例です。
ここでは正規分布に従う乱数を使って計算を行います。本来、モンテカルロ法は非正規分布にも対応できますが、今回はExcelの標準機能を使う関係で正規分布を用います。ただし、関数をカスタマイズすれば一様分布などにも変更可能です。
今回はあくまで実験的に「分散の加法性」が正しく再現されるかどうかを確認したいという意図もあり、正規分布を使って進めます。
まず1枚目の板の厚みを、正規分布に従う乱数で生成します。使う関数では、平均値10、標準偏差0.3の正規分布から乱数を出力するよう指定します。この数値は、セルの計算が更新されるたびに変化します。
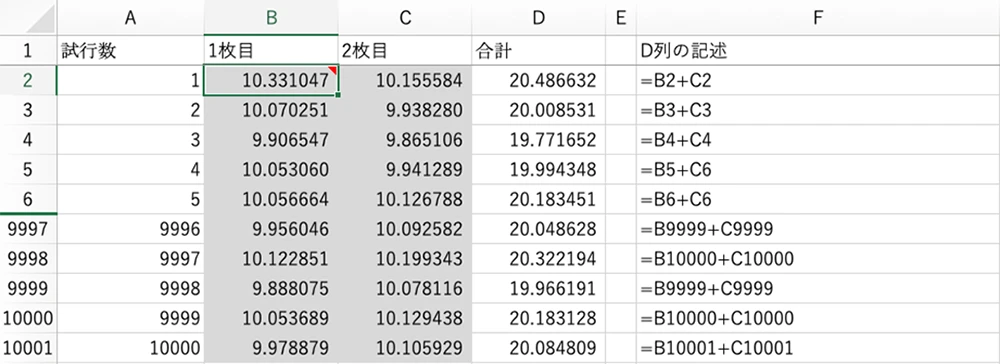
次に、2枚目の板についても同様に、同じ関数をコピーします。これで2つの厚みが乱数として得られました。
合計の厚みは、2つの乱数を足すだけです。これによって、板2枚を積み上げたときの合計厚さが出力されます。
さて、ここからがモンテカルロシミュレーションらしい「力技」の部分です。要するに、このランダムな組み合わせを非常に多数回、繰り返して統計的に分布の傾向を調べるのです。
今回は一万回分の計算を行います。乱数関数と加算式を下方向にコピーして繰り返していきます。手動で行うと大変なので、Ctrlキーを押しながら「下矢印キー」を使うと、一気に下まで移動できます。
さて、1万行分のデータを無事コピーできたでしょうか?10001行までで、ちょうど一万回になります。
では、この結果を少し詳しく見ていきましょう。隣のタブに、すでにヒストグラムを用意してあります。ここでは、度数分布表を用いて、1枚目の板の乱数データを区間に分けて集計しています。
初期の区間にはデータがほとんどありませんが、進むにつれて個数が増えてきて、100個を超えるピークの箇所も見られます。最大頻度の区間がピークとなり、全体の形としては「正規分布らしい」形状になっていることがヒストグラムからも確認できます。
もちろん、Excelではセルを更新するたびに乱数が再計算されますので、ヒストグラムの形も微妙に変化しますが、全体的には正規分布に近い滑らかな分布を描いています。
一枚目の板の厚みは、このように理想的な分布を示しています。そして、二枚目の板も同様で、平均が10、標準偏差が0.1という条件で生成されており、値はおおよそ9.7〜10.3の範囲に収まっています。わずかに外れ値もありますが、概ね期待通りの分布となっています。
「分散の加法性」が成り立つかどうかを確認
では、一枚目のシートに戻りましょう。ここで、シミュレーション結果のまとめを行いたいと思います。右側に、あらかじめ下書きとして配置しておいたセルがありますので、それを活用します。
まず、対象となる列(D列)の行数を確認しておきましょう。D2から始まり、10,001行目までデータがあるため、合計で1万個の乱数データが存在します。これを左側にコピーすれば、解析用の列が完成します。
さて、ここで「分散の加法性」が成り立つかどうかを確認してみましょう。
今回使用した正規分布の標準偏差は0.1なので、分散は0.1²=0.01です。板が2枚あるため、理論的には分散は0.01 + 0.01 = 0.02となり、合計の標準偏差は √0.02 ≒ 0.14 のはずです。
この理論値と実際のデータが一致するか、確認してみましょう。貼り付け用のセルを使って標準偏差を計算します。
一枚目の板(B列)で標準偏差を求めると、約0.0998、つまり0.1に非常に近い値になります。再計算のたびに多少変動しますが、毎回この周辺の値をとるはずです。
二枚目の板も同様に標準偏差を算出すると、こちらもおおむね0.1前後の値を示します。

平均値の確認
さて、平均値についても確認しておきましょう。どこかにすでに記載があるかと思いましたが、見当たりませんので、このタイミングで平均も計算してみましょう。
一枚目の板(B列)も二枚目の板(C列)も、いずれも平均値はおおよそ10付近に収まっており、分散は理論値である0.01前後となっています。
そして、2枚を足し合わせた合計の厚さ(D列)も、当然ながら平均20の周辺にあります。平均を取るとほぼ20、そして分散を計算すると理論値である0.02に近い値が得られます。
ここで注意すべき点として、D列の分散は「B列とC列の分散を足し合わせて得た値」ではなく、「加算済みの厚さ(D列)の1万個の実測値に対する分散」である、という点です。結果的に0.02前後になっていることで、分散の加法性が実証された形となります。
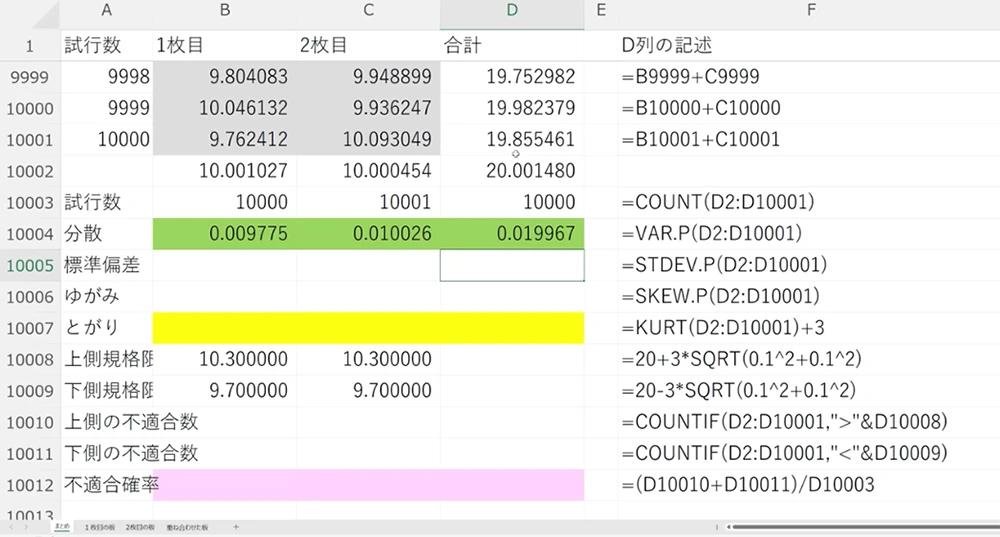
次に、標準偏差を求めてみましょう。ルートを取るか、Excelの STDEV.P などの関数を使えば求められます。標準偏差0.1の2枚の板を足し合わせたので、合計の標準偏差は理論上 √0.02 ≒ 0.14 となります。こちらもおおむねその通りの値が得られています。
ゆがみととがりの確認
さらに、分布の「ゆがみ」や「とがり」も確認しておきましょう。
「第18回 さまざまな確立分布」で Distribution Explorer を使用して解説した通り、ゆがみは、分布が右に寄っているか左に寄っているかを示します。正規分布であれば理論上0になるはずですが、今回もほぼ0に近い値となっており、理想的な対称性を保っていることが分かります。
とがりは、分布の鋭さを表します。正規分布であれば 3 ですが、こちらもそれに近い値を示しており、正規分布的な形状であることが確認できました。

実際の製品基準を適用した不良率の確認
次に、一枚目の板について実際の規格限界を設けてみましょう。平均10、標準偏差0.1、CP = 1 の条件から、公差は ±0.3 になります。つまり、上限は10.3、下限は9.7と設定します。
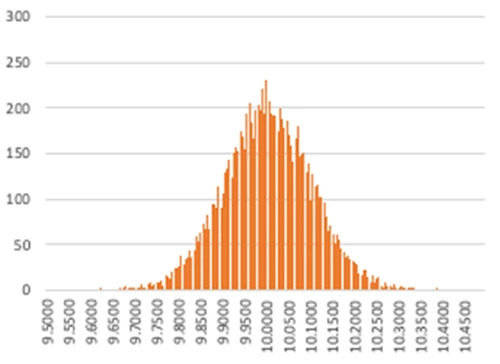
規格外の分布をヒストグラムで確認
この条件下で、1万個のデータのうち規格外となるもの、すなわち 10.3を超えるものと9.7を下回るものの個数 (=不良の数) を数えます。ヒストグラムでも確認できます。
Excelの COUNTIF 関数を使って数えると、10.3 の上限超えが17個、9.7 の下限未満もほぼ同程度、例えば18個程度になります。これは、正規分布が理論上±∞に広がるため、±3σを超える値も一定の確率で存在するためです。

重ね合わせた板に対する不良率
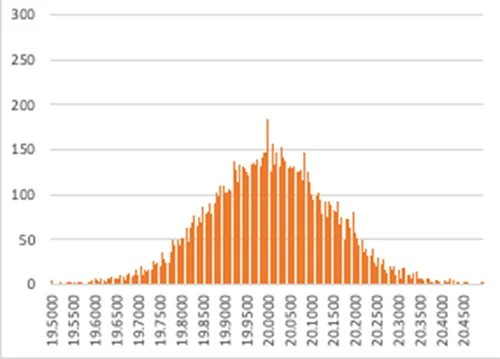
重ね合わせた板の分布のヒストグラム
では、2枚を足し合わせた場合の分布についても見てみましょう。平均は20、標準偏差は0.14です。ここでも同様に、±3σ、すなわち約20.42以上または19.57以下のデータが外れ値となります。ヒストグラムでも、外れ値は少ないながらも両端に存在していることが確認できます。
実際に数えると、上限超えが約14個、下限未満が12個などといった結果になります。これらは全体の中で 約0.35% の不良率であることを示しています。
この値は理論上の 0.27%(3σを超える確率)と近い値であり、わずかな差はモンテカルロ法によるランダムサンプリングに起因するものです。再計算するたびに多少のバラつきはありますが、概ねこの付近に収束します。
まとめ:モンテカルロ法の有効性と応用範囲
今回は正規分布を扱いましたので、理論的に分散の加法性を使えば、モンテカルロ法を使わずとも結果を得ることができました。しかし、非正規分布や掛け算の関係を含む場合など、理論的な手計算では扱いにくい一様分布や半円分布といった場合でも、モンテカルロ法で対応できます。
また、足し算や引き算だけでなく、掛け算のような非線形な関係でもシミュレーションできる点が、モンテカルロ法の特徴です。
というわけで、今回はExcelを用いてモンテカルロ法を実際に体験してみました。意外と簡単に実装できること、そして統計的な性質が理論と一致することが確認できたかと思います。