みんなの公差
#19 確率変数の和および差の分布
すきまばめ?中間ばめ?位置決めのピンや穴のはめあいはどう決める?
分布の再生性とは
正規分布する板と、別の正規分布する板を重ねたらどうなるか?を考えてみます。この答えは、不思議なことに「また正規分布」になります。この性質は「再生性」と呼ばれています。そして、この再生性があるからこそ、実は二乗和平方根が使えるということになります。
この再生性があるのは、実は正規分布と、あともう一つくらいしかありません。他の分布同士を組み合わせると、分布の形がどんどん変化していってしまいます。
たとえば、一様分布を繰り返し組み合わせていくと、最初は三角分布のような形になりますが、次第に正規分布に近づいていくことが知られています。
工場 Aで,10±0.3,Cp=1 →σ=0.1,μ=10の板を製造する。
工場 Bで,10±0.3,Cp=1 →σ=0.1,μ=10の板を製造する。
2つの工場で製造された板を重ねると…というお話です。
分散の加法性とは
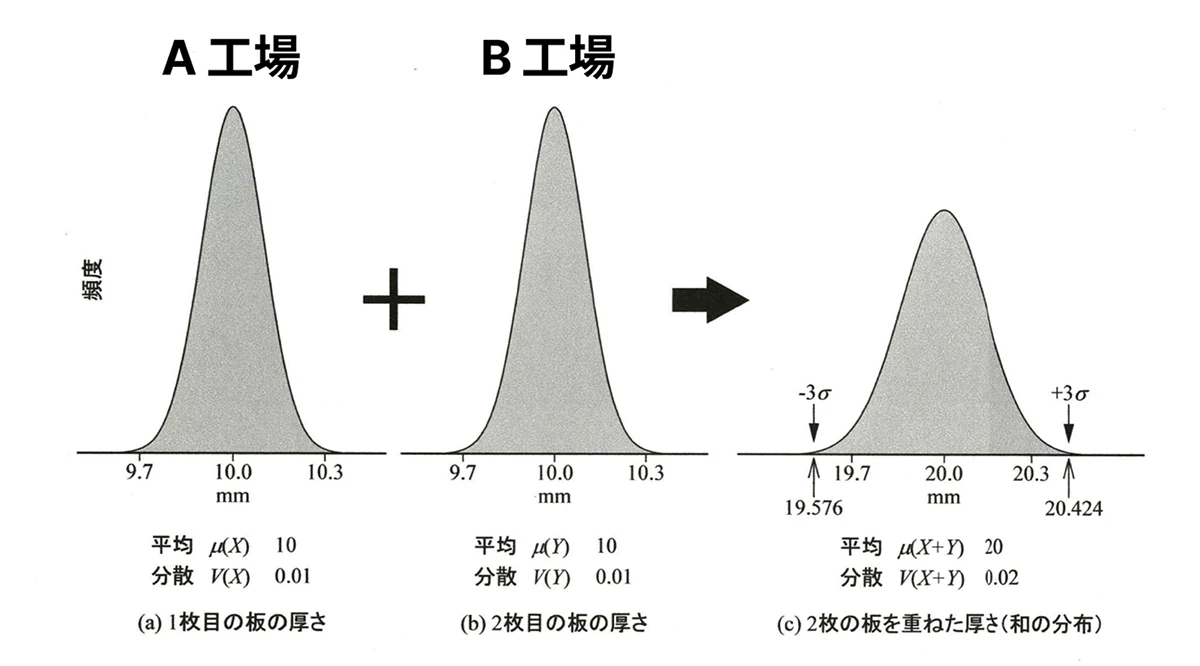
例えば、左の A 工場では10±0.3の範囲にあり、標準偏差が0.1の正規分布を考えます。このような分布では、わずかにグラフの外にはみ出している部分が数本見える程度で、つまり不良率はごくわずかです。
そして、B工場でもまったく同じ板を作っており、ここでは奇跡的に同じ分布になっているとします。
次に、この2つの工場の板を「組み合わせる」と考えます。厳密には「足し算」と言ってしまうと少し語弊があるのですが、例えばA工場で作られた9.8mmの板と、B工場で作られた10.1mmの板、あるいは10.2mmの板と10.25mmの板を組み合わせてみるというように、ランダムに組み合わせて厚さを測定します。
すると、その厚さの平均は20mmになります。これはそれぞれの工場で作られる板の平均が10mmであるため、当然の結果です。
そして重要なのは、こうしたランダムな組み合わせによって得られる厚さの分布もまた、正規分布になるという性質です。これはモンテカルロシミュレーションを行えばより納得できるのですが、同じような形状の分布を保ち続けるという特徴があります。
ここで、さらに注目すべき点があります。それは標準偏差についてです。今回、標準偏差を0.1に設定しました。すると分散はその二乗、すなわち0.01になります。
A工場とB工場のどちらも同じく分散0.01であれば、2つを組み合わせてできた厚さの分布の分散は、単純に足し合わせて0.02になります。つまり、分散は加法性をもつということが知られています。
分散の加法性を式で表すと
分散の加法性は下記のような式になります。
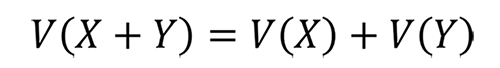
この式は少し分かりづらいかもしれませんが、例えば1つ目の工場の確率変数を X、2つ目の工場の確率変数を Y とした場合、それらを組み合わせたときの分散というのは、それぞれの分散を足してよい、ということになり、公差解析の中では重要な法則として知られています。
実際の現場では分散そのものを使うことはあまりなく、分散の加法性を標準偏差で表すと下記のような式になります。
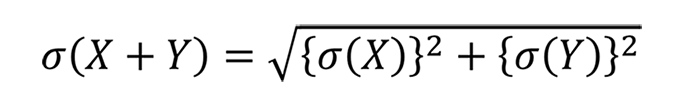
分散のルートを取ったものが標準偏差ですので、標準偏差に直す際には、まず分散を2乗の形で足し、それにルートをかけるという形になります。これが「二乗和平方根」の根拠になります。
分散の加法性が成立する前提条件とは?
この分散の加法性が成立するためには、いくつかの前提条件があります。まず第一に、「9.8と10.1」といった値をランダムに取り、組み合わせていくという無作為抽出が前提となっています。
たとえば、金型で作られるプレス部品やモールド部品のようなものでは、はじめは少し緩く作られ、次第に金型の摩耗によりきつくなっていくということがあります。このような場合は、無作為抽出とは言えず、分布が理論通りに綺麗に当てはまらない可能性があります。しかし、ここでは統計的な理論に基づいて話を進めているため、部品の組み合わせが無作為抽出であるという仮定を置いています。
次に2つ目の前提として、各確率変数が「独立」であることが求められます。この「独立性」を明確にするために、ここでは仮想的に「A工場」「B工場」と分けて、それぞれ別の工場で別々に作られた部品であるとしています(図1)。なお、数値はあえて同じにしていますが、理論上は「独立」であるという前提にしています。
では、独立でない場合とはどういうものでしょうか?たとえば、一方の板の厚さが変わると、もう一方も連動して厚さが変化するような関係があった場合、それは独立ではありません。このようなケースでは、分散の加法性は成り立ちません。
そして、3つ目の前提は、「確率変数の和の計算である」という点です。機械の分野においては、多くの場合、この「和」あるいは「差」のいずれかの演算で処理されることが一般的です。そのため、「和」または「差」であることが、分散の加法性を適用する上での必要条件になります。
「積」や「商」ではどうか、という疑問もあるかもしれませんが、機械の分野ではそういったケースはあまり見られません。しかし、電気回路のような分野では、変数が平方根の中に入っていたり、分母に入っていたりといった計算も見られます。こうした場合には、分散の加法性は成立しませんので注意が必要です。
さて、ここまでは板の厚さを組み合わせて、確率変数の「和」の計算をしてきました。ここからは、「差」の場合にはどうなるのか?という点についても考えてみましょう。
確率変数の差の計算の例
10.3±0.3Ⓔ Cp=1,k=0 の穴,
9.7±0.3Ⓔ Cp=1,k=0 の軸のすきまを考える。
上記を図で示すと次の図2のイメージになります。
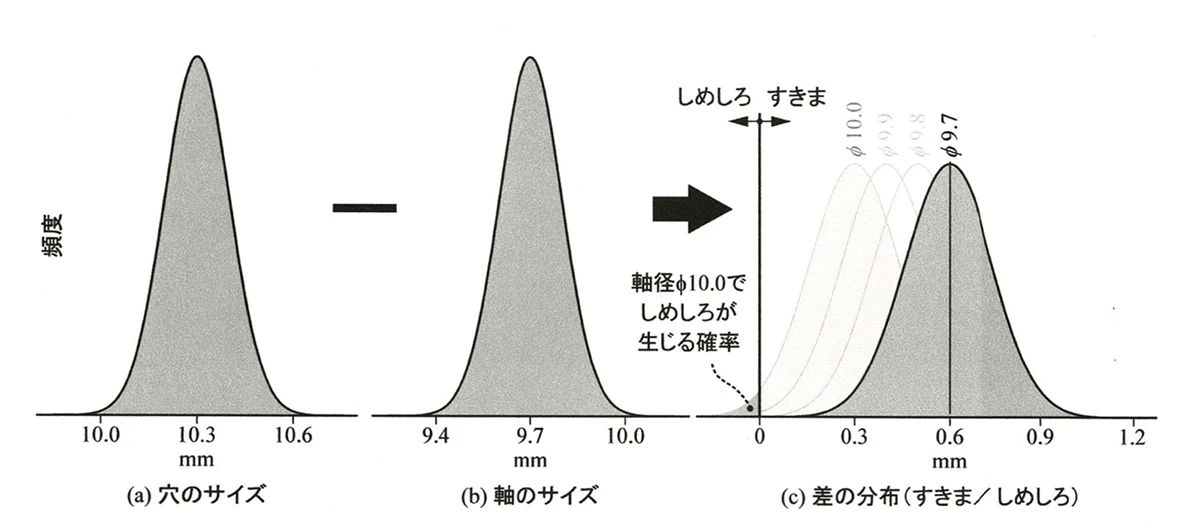
まず、左側の穴の方は図示サイズが10.3±0.3の範囲に分布しています。Cp=1であることから、99.7%が10.0以上10.6以下の範囲に入っていることになります。
対して、中央の軸の方は図示サイズが9.7±0.3の範囲に分布しており、Cp=1、k=0、99.7%がこの範囲の中に入っています。k=0 というのは、“かたより”がない状態で中央に位置しています。
この2つの分布を「引き算する」といっても、これは直接的な演算ではなくあくまでイメージとして捉えてください。たとえば、10.3の穴と9.5の軸があった場合、「すきま」がどのような分布になるかを考えます。
ここではさらに、軸の図示サイズ(現在は9.7)を0.1ずつ大きくしていった場合を想定してみます。
現状では、すきまが必ず生じる「すきまばめ」となっています。しかし、軸を徐々に太くしていくと、「しめしろ」が発生するような「中間ばめ」に入り、やがて「しまりばめ」へと移行していきます。
この変化にともなって、「しめしろ」が生じる確率を少しずつ追っていきたいと思います。
標準偏差を求める
さて、「10.3 ± 0.3」のような仕様から、ここでは標準偏差を求めてみたいと思います。
10.3±0.3Ⓔ Cp=1、k=0 の標準偏差σh
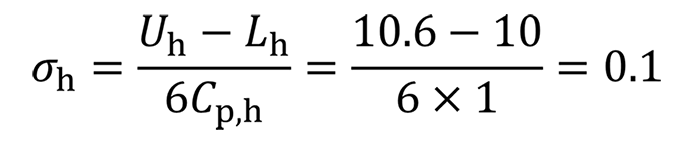
ただ、いきなりこのような式を提示されると、「なんのこっちゃ?」と感じる方や、少しアレルギー反応を起こす方もいらっしゃるかもしれません。そこで、まずは Cₚ の式 を思い出してみましょう。
Cₚ とは何かというと、分母が「6シグマ」、分子が「公差」でした。すなわち、下記の式になります。
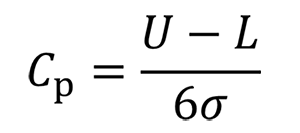
同様に、軸の方(s)についても下記の式にて計算ができます。
9.7±0.3Ⓔ Cp=1,k=0 の標準偏差σs
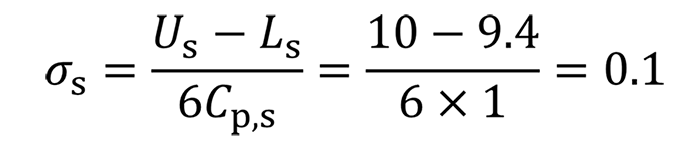
上記より、どちらも等しく標準偏差が 0.1 に設定されていることが確認できます。
ちなみに、添え字の h はホール(穴)、s はシャフト(軸)を表しています。これらの標準偏差は、後ほど差の分布を扱う際に重要になってきます。
分散は足せるので、標準偏差であれば二乗して足し、その後ルートを取れば計算できます。このように計算すると、結果として√0.02になります。
すきまの標準偏差σは,分散の加法性を用いて以下のとおり。
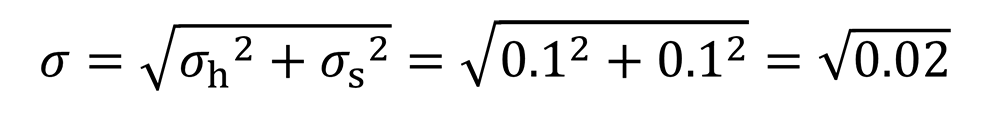
10.3±0.3Ⓔ, 9.7±0.3Ⓔのすきまの平均μは,以下の通り。
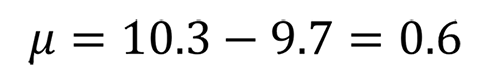
しめしろが生じる確率とは

このxが0、μが0.6であるという意味を、グラフで確認してみたいと思います。
まず、穴のサイズはこれまで扱ってきたとおり、10.0 mm±0.3 mmです。軸のサイズは9.7 ±0.3 mmとなっており、これらの部品をそれぞれピックアップしてすきまを測定し、直径の差を調べると、平均は0.6 mmになります。
この図においては、左のグラフが穴の分布、中央が軸の分布、そして右のグラフがその差、つまりすきま(またはしめしろ)の分布を示しています。それぞれの分布の中心、すなわち最も度数の多い部分が、差の分布においては0.6 mmの位置に最も大きなピークとして現れることが視覚的にも理解できます。
ここで確認したいのは、「すきまが0.6 mmである」というのは平均ですが、すきまが0 より小さくなる場合、しめしろが生じます。分布の右端ではまだすきまがありますが、これが小さくなってゼロになるあたりから、軸が穴にぴったりはまる、すなわち「しめしろが生じる」状態になります。
ただし、この図からも分かるとおり、すきまがゼロ以下となる確率は非常に小さく、事実上ほとんど起こらない程度の値となっています。
それでは、しめしろが生じる確率を求めていきます。標準化を行うと、Zの値は -4.24 になります。

しめしろが生じる確率は、正規分布表を用いて求めると 0.001% という非常に小さい値になります。
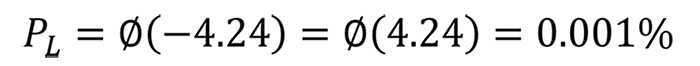
次に、軸の寸法だけを調整する場合を考えます。
軸の直径を9.8 mmとし、わずかに寸法を大きくしてすきまを減らすことにします。このとき、すきまの分布は左に0.1 mmシフトします。図中にも薄く示されているように、分布の中心が左に移動することで、しめしろが生じる確率がわずかに増加します。
再び標準化を行うと、Z = -3.54 となり、確率は 0.02% になります。先ほどと比較すると、確率が一桁大きくなっていることがわかります。
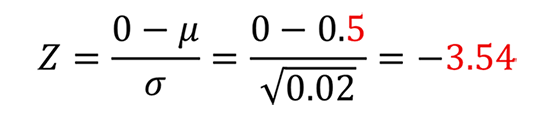
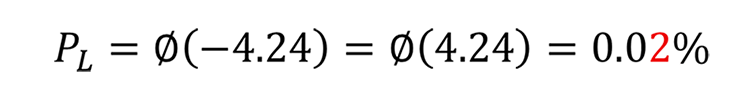
さらに、同様の操作を繰り返して、軸の直径を9.9 mm、9.95 mm、10.0 mmと段階的に大きくしていくと、すきまの分布はさらに左に移動し、しめしろが生じる確率は段階的に増加していきます(図2 の右の図を参照)。
すきまばめ/中間ばめ/しまりばめ? しめしろが生じる確率をグラフで確認
このしめしろが生じる確率をグラフにまとめました。
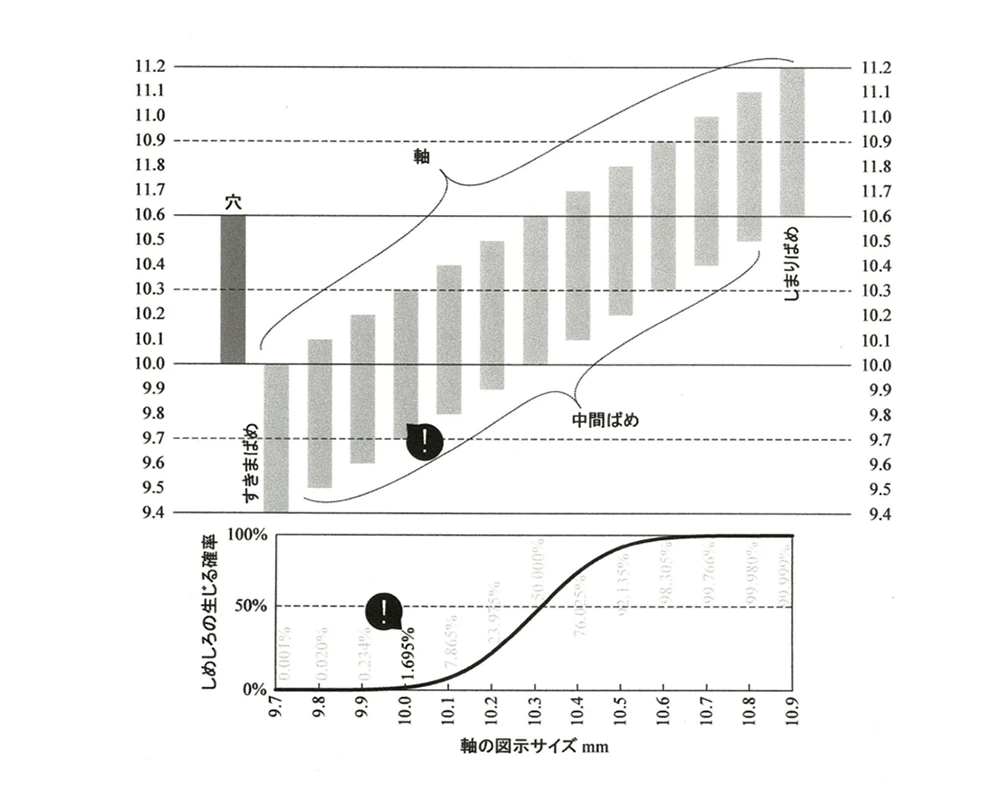
図3の上のグラフは、機械系の教育などでよく見られる「サイズ許容区間」と呼ばれるものです。それぞれの部品、穴と軸がどのような寸法分布を持っているかを視覚的に示すものであり、はめあい関係を分析する際に用いられます。
最初の設定では、穴は直径10.0±0.3 mm、軸は9.7±0.3 mmです。この場合、軸と穴の寸法範囲は完全に重なっておらず、常にすきまが生じる「すきまばめ」の状態になります。このとき、しめしろが生じる確率はわずか0.001%でした。
次に、軸の直径を0.1 mm大きくして9.8 mm±0.3 mmとした場合、軸の分布が少し右側に移動し、穴の分布との一部重なりが生まれます。このとき、一部の軸が穴にぴったり入る「中間ばめ」の状態が現れ、しめしろが生じる確率は0.02%に増加します。
さらに軸の直径を0.1 mmずつ増やしていくと、例えば9.9 mmでは0.234%、10.0 mmでは1.695%と、しめしろが生じる確率が少しずつ増加していきます(図3の下のグラフ参照)。これは、サイズ許容区間の中で軸の分布が穴の分布と徐々に重なっていくためです。
やがて、軸の中心が穴の中心に一致する10.3 mmのとき、しめしろが生じる確率とすきまが生じる確率がともに50%となります。
この後も軸の直径を増やしていくと、確率はさらに上昇し、最終的に10.9 mmとなると、穴と軸の関係はしまりばめとなり、必ずしめしろが生じる関係になります。ただし、正規分布を前提としているため、ごくわずかですが例外的にすきまが生じる可能性も理論上存在します。
まとめ
このように、しめしろ(またはすきま)が生じる確率の変化を追ってみると、位置決めのピンや穴のはめあいにおいて、「どのような設計が望ましいか?」ということを、改めて考えさせられます。
一般に、確実な組立を実現するために「すきまばめ」を選択することが多いですが、その一方で位置決めの精度を重視する場合には、できるだけ「がた」を抑えることが求められます。
このとき、「中間ばめ」を選択することで多少の組立性を犠牲にしつつも、がたの抑制に寄与する可能性があると考えられます。もちろん、組立ができなければ意味がありませんので、すきまばめを選ぶことにも合理性がありますが、それによりがたを増やすことにも繋がります。
実際の設計現場では、精度と組立性のバランスをどう取るか?が重要です。
各企業や現場の経験、ノウハウに基づき、最適な許容域を見極めることが求められます。
以上、今回は「確率変数の和および差の分布」に関する解説を行いました。