みんなの公差
#18 さまざまな確率分布
三角分布や半円分布、一様分布など、さまざまな分布について紹介
さまざまな確率分布が用いられる背景
これまでは主に正規分布のみを扱ってきましたが、実際の工程から得られるデータが、必ずしも正規分布に従っているとは限りません。そうでないケースも、実は多く存在しています。
たとえば、三角分布や半円分布、あるいはサイコロを振ったときのような一様分布など、他にもさまざまな分布が考えられます。
今回は、このような多様な分布をいくつか紹介し、もし対象となるデータが正規分布に従っていない場合には、これらの分布を用いて公差解析する方法がある、ということをご説明したいと思います。
「Probability Distribution Explorer」での確率計算
今回は、ソフトウェアを使ってみたいと思います。使用するのは、「Probability Distribution Explorer」というソフトウェアです。これはフリーソフトで、SDI Japan 様のページからダウンロード可能です*注1
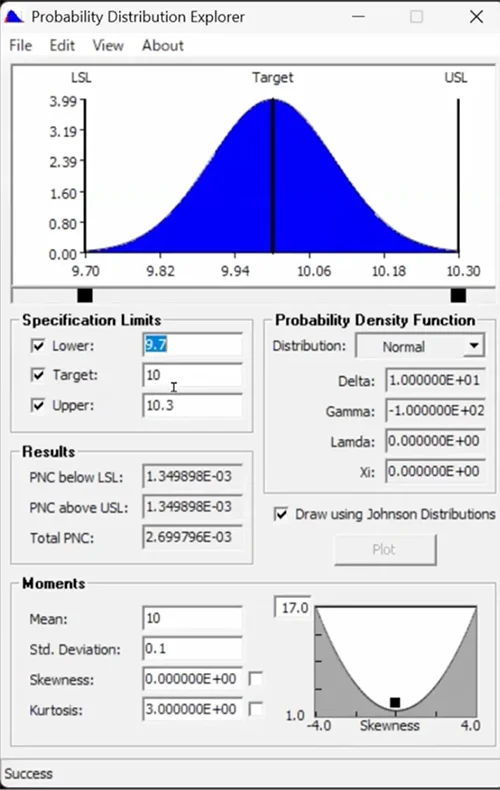
ここでは、これまで例として取り上げてきた「10 ± 0.3」という数値を使っています。つまり、Target (目標値) が10で、Upper (上限) が10.3、Lower (下限) が9.7という設定です。
このソフトウェアでは、設定した公差範囲(10.3以上、または9.7以下)を超える確率、つまり規格外となる確率を計算してくれます。
すでにご説明した通り、この規格外の確率は約0.135%程、上側と下側に存在します。つまり、両端を合計すると約0.27%程度になります。これはどういうことかというと、おおよそ1000個中に2.7個、つまり1000個作ると2〜3個程度が規格外になるという計算になります。
この計算は、正規分布に基づいており、正規分布表があれば手計算でも求めることが可能です。
正規分布以外の分布について
ここからは正規分布以外の分布についてご説明します。三角分布や半円分布、一様分布など、さまざまな分布がありますが、これらは「β2 (ベータ)」という指標によって定義されています。
実はこの β2 という1つの指標で、それぞれの分布の形が定義されています。ちなみに、正規分布の場合の β2 の値(尖度とも呼ばれます)は「3」です。
この指標は、Probability Distribution Explorer では「Kurtosis(カートシス)」と表示されています。日本語では「とがり」です。この数値を変更することで、分布の形を変えることができます。
半円分布の場合
たとえば、半円分布のときには、β2 = 2 となります。Kurtosis の値が小さいほど山がなだらかで、分布が広がっていることを意味します。
Upper(上限)とLower(下限)がかなり内側に設定されているため、規格内に入る確率が非常に高くなっています。そこで、たとえば Upperを 10.8、Lower を 9.3 のように少し広げて設定すると、それに応じて規格内に入る確率が変化します。このソフトウェアは、その確率を自動で再計算して表示してくれます。
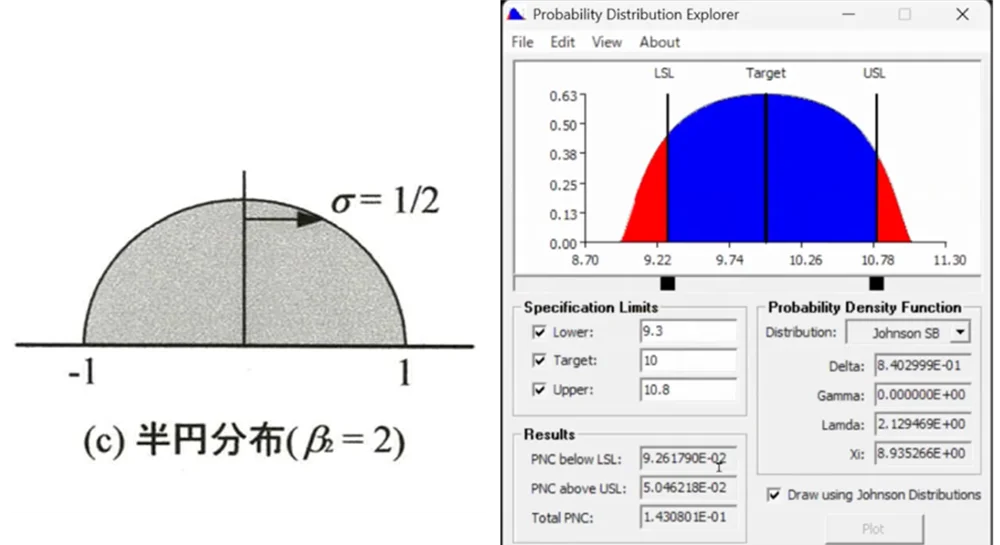
実際に、どのような分布をしているかは、測定してみなければ正確には分かりません。ただし、加工方法の種類によって、ある程度は分布の形が決まっている場合もあります。そうした情報があれば、不良率の計算もより正確に行うことができます。
逆に言うと、毎回「正規分布」を前提にしてしまうと、想定外に不良率が高くなってしまい、思わぬトラブルにつながる可能性もあります。
一様分布の場合
ここで「Kurtosis」の値を1.8に変更してみましょう。これによって、一様分布に近い形になるはずです。実際に変更してみると、完全に四角い分布にはなりませんが、ほぼ一様分布に近い形が描かれます。
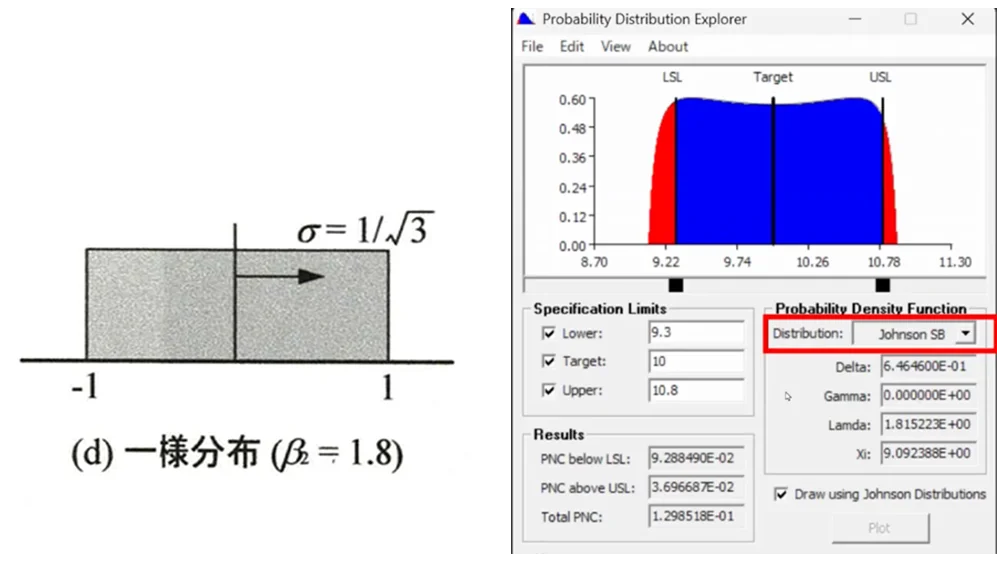
おそらくソフトウェアの仕様上、数学的に完全な直角を描くのが難しいため、近似的な形状になっているのだと思われます。この分布は「Johnson SB」と呼ばれるものです。
この分布は、平均や標準偏差だけでなく、ゆがみやとがりも考慮して形を決定できるのが特徴です。
三角分布の場合
次は「三角分布」です。三角分布では、「Kurtosis」が2.4になります。これもソフト上でクリックすれば表示されます。
三角分布では、山の頂点や端の部分がやや丸みを帯びていますが、概ね三角形の形状になります。
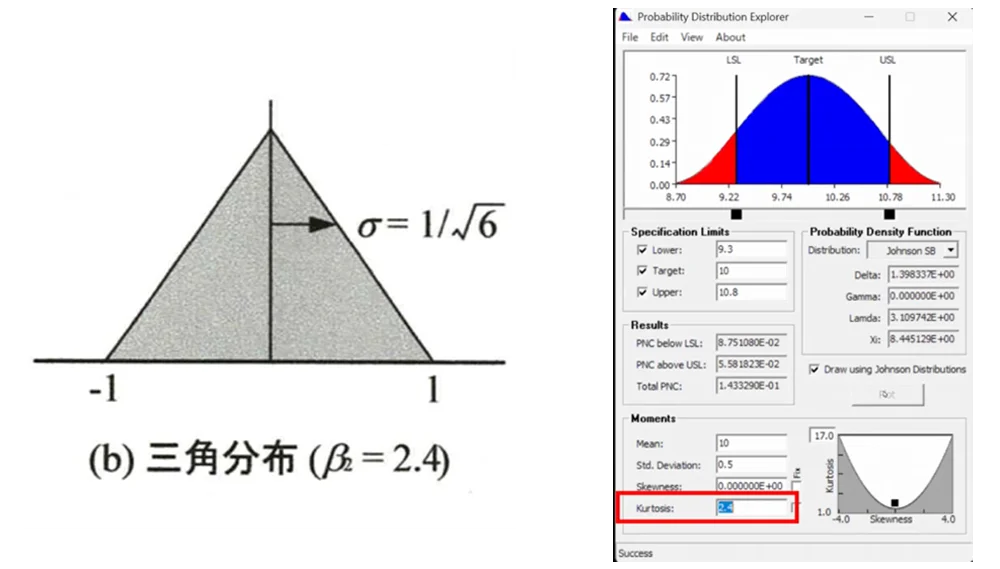
そのほか、統計でよく登場する「t分布」や、二つの一様分布を重ねたような形になる「台形分布」なども表示できます。さらに「ベータ分布」は、非常に自由度の高い分布で、二つのパラメータを調整することで、山を尖らせたり、左右に偏らせたりすることが可能です。最後に紹介するのは、先ほども少し触れた「ジョンソン分布」です。SU型やSB型などがあり、とがりやゆがみといった特性を柔軟に反映した分布を描くことができます。さまざまな実データに対応できる、非常に便利なモデルです。
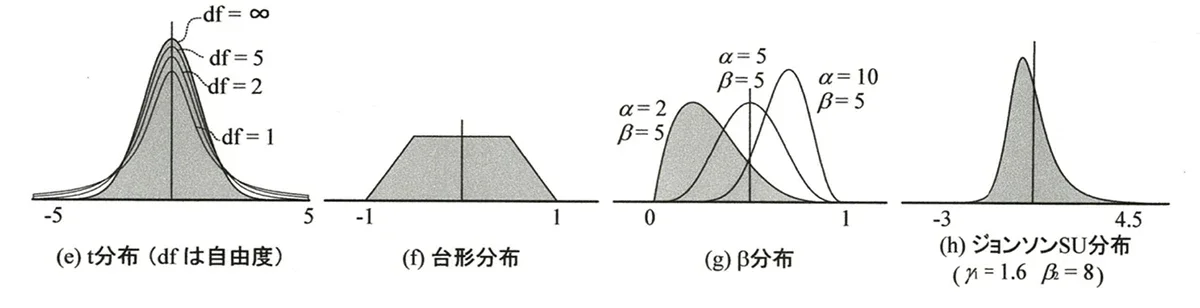
ここでは先ほどまで、「Kurtosis (とがり)」を表す値のみを調整していましたが、今回はもう一つの指標である「Skewness (ゆがみ)」についても試してみたいと思います。
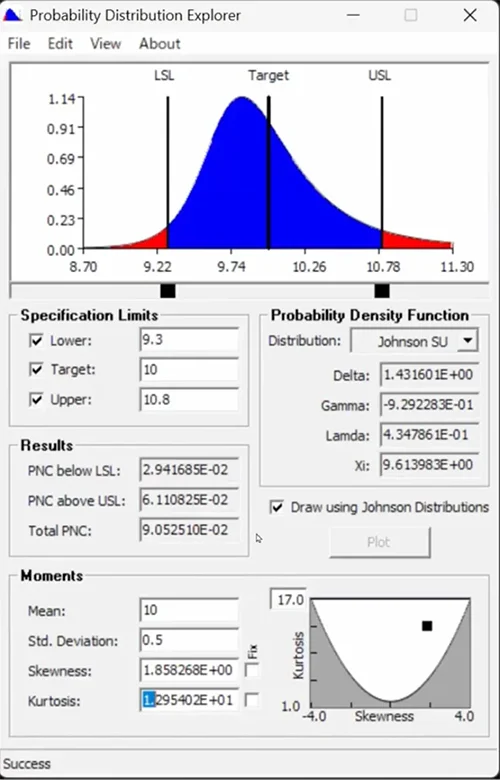
この部分は、ソフトウェア上でクリックすることで値を動かすことができます。
Kurtosisは、グラフ上で言うと山の高さがどれくらい鋭く上に突き出ているかを示す指標で、値が大きくなるほど山が鋭く尖った分布になります。
一方、左右の非対称性を示すのが「Skewness (ゆがみ)」です。この値を調整することで、分布が右寄りになったり左寄りになったりします。
つまり、このソフトはとがりとゆがみという2つの数学的な指標を用いて、実際の分布形状をより正確に表現できるようになっています。
このような機能を使って、自分のデータがどのような分布に近いのかを視覚的に確認できるのは、とても有用だと思います。ぜひ、皆さんも実験的に触ってみてはいかがでしょうか。
というわけで、さまざまな確率分布の形を見て、自社の製造工程に合った分布モデルを適用することの重要性についてお話しました。