みんなの公差
#17 工程能力指数(Cp・Cpk)
工程能力指数の求め方とかたよりを考慮した工程能力指数 (最小工程能力指数)を解説
工程能力指数とは
工程能力指数とは、ここに示されている式で表される1つの指標のことを指します。この指標は言葉で私が定義するなら、「公差に対する製造の余裕を表す比」であると思います。
詳細につきましては、JIS(日本工業規格)の標準を参照いただければと思いますが、まずは皆さんご自身で「工程能力指数とは何か?」という問いに対し、自ら定義を考えてみていただきたいと思います。そうすることで、この概念に対する理解が一層深まるはずです。
規格幅と標準偏差の関係、およびCpの求め方とその意味
Cpは以下の式で求められます。ここでの分子が公差になります。
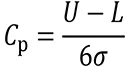
工程能力指数の説明に入る前に、使用される記号や数値の意味について触れておきます。
U:上側規格限界
L:下側規格限界
U-L:規格幅
6σ:参照区間
たとえば、寸法が「10 ± 0.3」であれば、上側規格限界は10.3、下側規格限界は9.7となり、規格幅は公差にあたるもので0.6になります。
6σとは参照区間と言われます。実際に部品を作って標準偏差を測ってみて、その6倍の範囲が参照区間と言われています。
そして、分母と分子にそれぞれ役割を当てはめるとすれば、
分子=設計担当
分母=製造担当 ということになります。
例題1
10±0.3の板を例にして,
(a) σ=0.15 (b) σ=0.1 (c) σ=0.075 の場合を比較してみましょう。
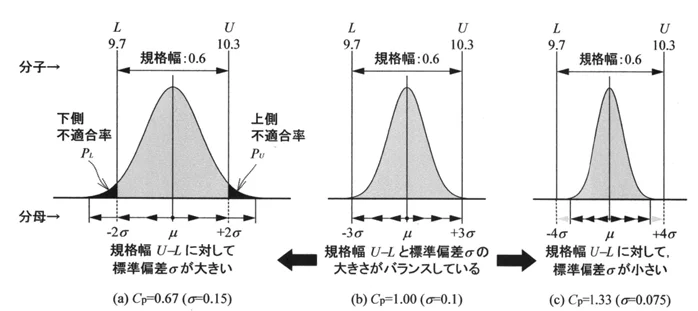
(a) Cp=0.67 (σ = 0.15) の場合
規格幅は、0.6になります。つまり、上限が+0.3、下限が-0.3です。
このとき、シグマが0.15であるため、±1シグマの範囲は±0.15、±2シグマで±0.30、±3シグマで±0.45になります。
このように、±3シグマの範囲(全体で0.9)は、規格幅(0.6)を超えてしまっており、分布の両端が規格外に出てしまうことになります。
分布が広いため、不良品が一定割合で発生してしまう状態です。
このとき、Cp(工程能力指数)を計算すると以下のようになります。
Cp = (10.3 - 9.7)/(6 × 0.15) =0.67
(b) Cp=1.0 (σ = 0.1) の場合
次に、同じく規格幅0.6に対して、σが0.1の場合を見てみましょう。
このときの Cp は以下の通りです。
Cp=(10.3 - 9.7)/(6 × 0.1) =1.00
動画でも説明しているとおり、不良率は両側で0.27%程度に過ぎず、不良品は非常に少ないことになります。
規格幅 U-L と標準偏差σの大きさがバランスしていると言ってもよいと思います。Cp=1.0 というのが1つの指標になると思います。
(c) Cp=1.33 (σ = 0.075) の場合
さらに標準偏差が小さくなり、0.075の場合を考えます。
分布の幅はどんどん小さくなっていきます。規格幅に対して標準偏差が小さく、分布幅が狭い状態となります。
このときの Cp は次の式で求められます
Cp=(10.3 - 9.7)/(6 × 0.075) =1.33
このように、Cpが1を超えると、分布が規格幅に対して十分に収まっており、製品のばらつきが少ない、つまり品質に余裕がある工程であることが分かります。
逆に、Cpが1を下回る場合は、規格の幅に対して分布が広くなりすぎて規格外の不良品が増加することを意味します。
ポイント:
- Cp < 1:ばらつきが大きく、不良品が出やすい(例:シグマ=0.15)
- Cp = 1:ちょうど規格幅に収まる状態(例:シグマ=0.1)
- Cp > 1:ばらつきが小さく、余裕のある工程(例:シグマ=0.075)
ここでひとつ例題を用意してみました。実際に関数電卓や Excel などで計算をしてみると理解が深まると思います。
例題2
厚さ10±0.2で指示された板が多数ある。
板厚が平均値 μ=10、標準偏差 σ=0.05 で正規分布しているとき、工程能力指数 Cp を求めよ。
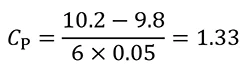
数字を当てはめてみると次の式になります。
一般的に 1.33 という数字は工程能力指数として十分と言われています。
Cpk:かたよりを考慮した工程能力指数 (最小工程能力指数)
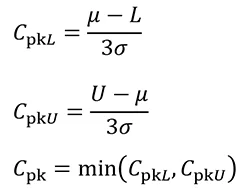
Cpkは CpkL、CpkUの小さい値を採用
次に、かたよりを考慮した工程能力指数(最小工程能力指数)についてご説明します。
この指標はCpkと呼ばれます。
Cpkは CpkL または CpkUのいずれか小さい方の値を採用します。
このように、Cpkは規格上限または下限のどちらかに平均値μが近づいている場合、その方向の余裕を基に評価します。
これにより、製品の分布が中心に対してかたよっているかどうかを把握することができます。
例題3
10±0.3の板を例にして、σ=0.1、
(a) σ=0.1, μ=9.8
(b) σ=0.1, μ=10.0
(c) σ=0.1, μ=10.1 を比較しましょう。
図をご覧いただくと、理解が早いかもしれません。
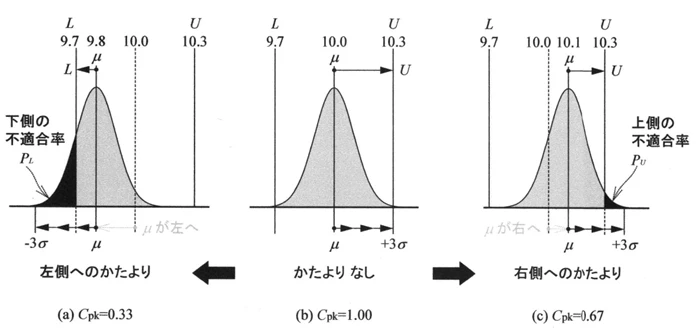
(a) μ = 9.8 の場合:左側へのかたより
まず μ = 9.8 の場合、規格の中央(目標値)である 10.0 に対して、中心が大幅にズレているのがわかると思います。このとき、分布の多くが左(下限)側に寄るため、不適合品は下限値(L = 9.7)を下回る領域に多く現れます。
一方、上限(U = 10.3)を超えることはほとんどなく、問題にはなりません。
このように、分布が一方に偏っている場合は、かたよりを考慮した工程能力指数 Cpk を用いて評価します。このケースでは CpkL を使用します。
もしこれを単に Cp で評価すると、分布全体のばらつきのみを考慮するため、Cp = 1.0 となり、かたよりを評価できない恐れがあります。よって、Cpk を用いることでかたよりを反映した適切な評価が可能になります。
(b) μ = 10.0 の場合:かたよりなし
次に μ = 10.0 のケースです。これは規格の中心に平均値が位置しており、分布にかたよりは見られません。
このときは、CpkL = CpkU = 1.00 となり、工程が理想的にバランスしていることを示します。
(c) μ = 10.1 の場合:右側へのかたより
最後に、μ = 10.1 のケースです。公差の中央(10.0)から平均値が右に 0.1 シフトしており、分布の多くが上限側に近づいています。
この場合は、上限を超える不適合品の割合が増えるため、CpkU を使って評価します。
10.3-10.1/3σ = 0.67 Cpk は 0.67 となります。
このように、平均値が右にずれることで、上限側の不適合率が高くなることが Cpk によって明確に表されます。
Cpk を使うことで「どれだけ工程に余裕があるか」や「どちら側に不適合品が出やすいか」を把握できます。
例題4
厚さ10±0.2で指示された板が多数ある。
板厚が平均値 μ=10.05 、標準偏差 σ=0.05 で正規分布しているとき、かたよりを考慮した工程能力指数 Cpk を求めよ。
ここでは CpkU と CpkL を両方計算してみます。
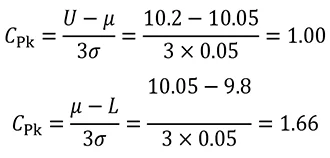
CpとCpkの関係
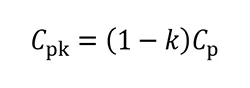
工程能力指数 Cp と、実際の工程能力を示す Cpk の関係について説明します。まず、両者の関係は右記の式で表されます。より詳細な式は、『幾何公差・公差解析実践ハンドブック』の中に記載していますのでそちらもご参照ください。
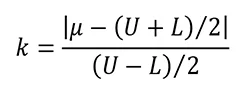
ここで出てくる「k」は、「かたより度」と呼ばれる指標/比率です。工程の平均値が目標値(規格の中心)からどれだけずれているかを示す比率で、右記の式で定義されます。
かたより度 (k) とは
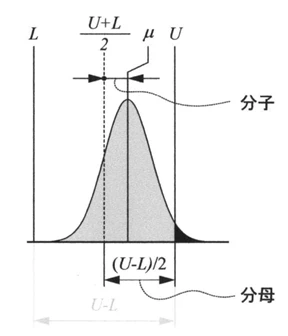
かたより度 (k) を図式化
上記の式を見ると一見複雑に見えるかもしれませんが、図やグラフと併せて見ると直感的に理解しやすくなります。工程の中心(μ)が規格の中心からずれているほど、かたより度 k が大きくなり、その結果として Cpk は Cp よりも小さくなります。
つまり、いくら分布のばらつきが小さくCp が高かったとしても、工程が中心から外れていれば Cpk は下がり、実際の品質の評価は厳しくなります。
この関係を正しく理解することで、単に分散を小さくするだけでなく、工程の中心を適切に保つことの重要性がよくわかると思います。
工程能力指数(Cp、Cpk)は、製造工程の品質を客観的に評価し、改善の方向性を見出すために欠かせない指標です。この後、工程能力指数 (Cp、Cpk) を考慮に入れた公差解析も解説していきたいと思いますので、お楽しみに。
工程能力指数(Cp・Cpk)を動画で解説!
#17 工程能力指数(Cp・Cpk)
こちらもおすすめ!「工程能力指数」はいくつ必要?公差の“へそくり”は隠さず出そう
「工程能力指数」を気にするのはどの部門?日本企業にディメンショナルエンジニアが必要な理由とは
「みんなの公差」では公開できない本音を語るオフレコ話を Web ページでご紹介しています。「第17回 工程能力指数」収録後トーク、是非お読みください。