コラム用語集
CAE を用いた最適化とは?最適化のメリットや最適化アルゴリズムをわかりやすく解説
このページでは CAE と最適化を組み合わせるとはどういうことか、どんなメリットがあるかを、初心者にもわかりやすく説明します。また、最適化を実現するための各手法や最適化アルゴリズムについても解説したのち、最適化をはじめたい設計者に有益な学習コンテンツについてご紹介します。
最適化とはどういうことなのかをわかりやすく解説
CAE の最適化とはさまざまな解析条件の組み合わせの中から目的の解析を達成するため、最良の組み合わせに辿り着くことです。目標値に対する最適化の場合は、目標値との差などをできる限り最小化します。例えば「固有振動数を○○Hzに出来るだけ近づけたい」などが挙げられます。
……とこのような説明が一般的にはなりますが、CAE の解析のみでも複雑な設定が必要となるため、初心者にはなかなかイメージが湧かないのが現状かと思います。
そこで、まずはイメージをつかんでいただくため、「最適化」とはどういうことかを3人の少年の山登りに例えてみましょう。
とある晴れた日、3人の少年が山登りをすることになりました。あなたは3人のうち、どのタイプでしょうか?

最適化への道のり Case1 :うっかり者のたけし君
いつも思いつきで心のままに行動するたけし君。いつものとおり、特に準備なしの行動。見えている頂上に向かって、一生懸命歩きました。 途中で道に迷いながらもやっとの思いで頂上に着きましたが、そこからはもっと高い山が見えるではありませんが。目的はそこであっていたのでしょうか?その上、雨まで降ってきてしまいました。

最適化への道のり Case2 :ちゃっかり者のひろし君
まわりの状況を的確に理解しナイスな判断をするちゃっかり者のひろし君。ひろし君は、山登りの前日、おじいちゃんからアドバイスを受けてきたようです。

さて、今日はどうでしょう?
①雲が一番高い山だけに掛かっている⇒ 絶対に雨は降らない?
②分かれ道は右・左・右・左の順番⇒ 必ず一番高い山の頂上に着く?
③この時期は雨は降らない&気候も穏やか⇒ 軽装でも十分登山ができる?
おじいちゃんのアドバイスを受け、「今日は大丈夫!」と信じて山に登りました。結果的に頂上にはなんとか到着できたようですが…
- ホントにいつもアドバイス通りで大丈夫でしょうか?
- 道順はそれだけなのでしょうか?
- 「教えられた道順」でひろし君は楽しめたのでしょうか?

最適化への道のり Case3 :しっかり者のひでき君
いつも用意周到なしっかり者のひでき君。今日の山登りためにいつも通りしっかり準備をしてきたようです。 今回のひでき君の目的は「気分転換のための軽いエクササイズ」。
ひでき君は地図とガイドブックを読み、そしてインターネットで当日の天気を調べました。
観光ポイント:
・歩道沿いの花畑
・ケーブルカーからの絶景
・初級~上級者向けのロッククライミング
予想した時間通り、目的の頂上についてお弁当を食べることができました。ひでき君は山登りの途中も、きれいな花畑で初夏の訪れを感じながら、気持ちの良い汗を流すことができたようです。

さて、あなたはどの子が一番賢明だと思いますか?
ものづくりにおける CAE の最適化もこの3人の例と全く同じです。目的を達成するための最適な手段を選ぶために「ものづくりにおける地図を持つこと」が大切なのです。
最適化の近道!ものづくりにおける地図を持つには
最適化の第一歩は設計空間の見える化
最適化の近道となる、ものづくりにおける地図を持つには、まず「設計空間を見える化すること!」が非常に重要です。
設計空間とはすなわち、設計パラメータの組み合わせで作られる集合(=空間)を指します。ものづくりの地図を持つには、できる限り多くの実験データを集めて、それを可視化する必要があります。
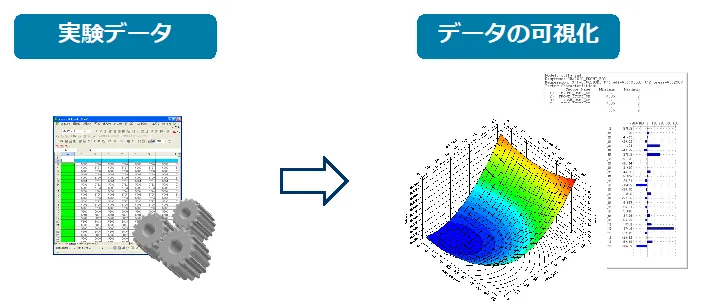
しかし、実験していない部分のデータ取得は困難であり、すべての実験データを取得するには時間とコストがかかります。そこで活躍するのが、CAE です。
まずは CAE を最大限活用しましょう
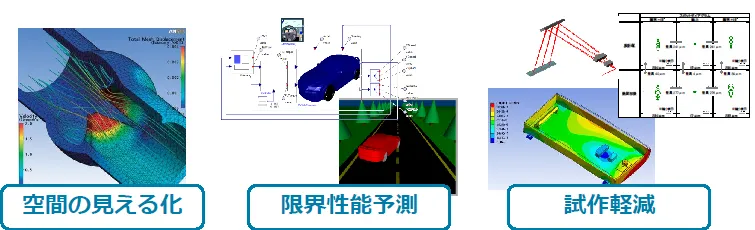
CAE (Computer Aided Engineering) を活用することで、コンピュータ上での仮想実験が可能となります。CAE は実験コスト、時間の削減に繋がります。空間を見える化し、現実世界では難しいさまざまな性能予測が可能になります。また、設計のフロントローディングや試作の軽減にも役立ちます。CAE についての詳細はこちらのページもご覧ください。
CAEと最適化ツールを組み合わせると嬉しい訳
CAE プロセスを自動化して開発期間を短縮できる
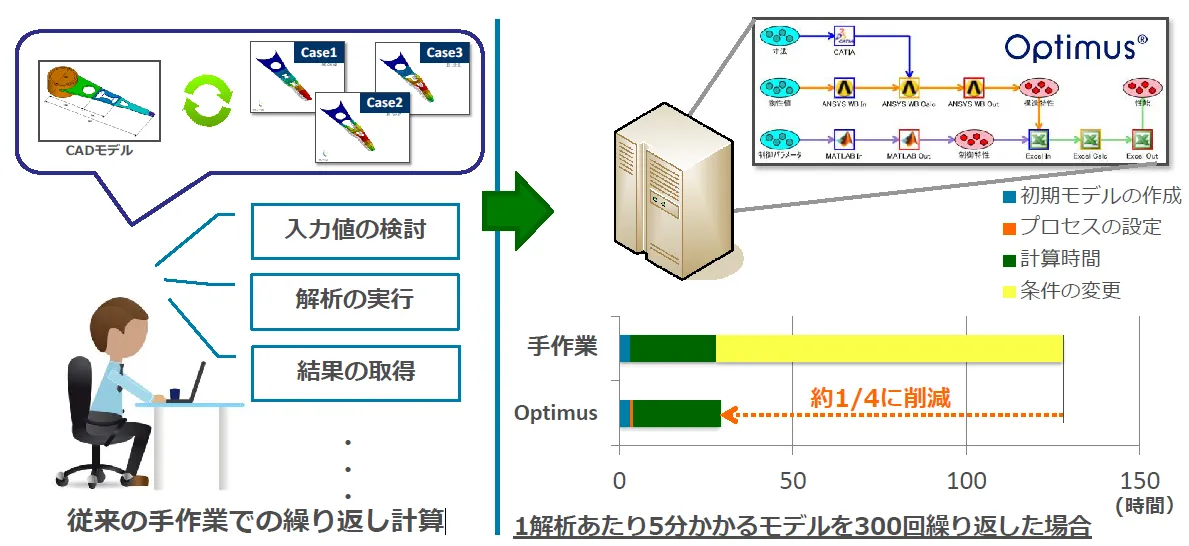
CAE の解析は時間がかかるものです。1解析あたりに5分かかるモデルの設定を微変更して300回繰り返し計算をしなければならない場合、150時間もの時間がかかってしまいます。
最適化ツールを活用すると、この繰り返し計算のプロセスを自動化することが可能です。モデルや解析条件の変更、結果の整理や評価等の非効率的な作業をすべて削減できます。
また、最適化計算に必要な繰り返し計算は、分散処理により短期間で収束させることも可能です。これにより、開発期間の短縮を実現できます。
情報を直感的に理解するための可視化が可能に
可視化することで見るべき情報が一目でわかるようになります。下記の情報は同じ解析結果を示していますが、どちらの方が見やすいかは明らかかと思います。
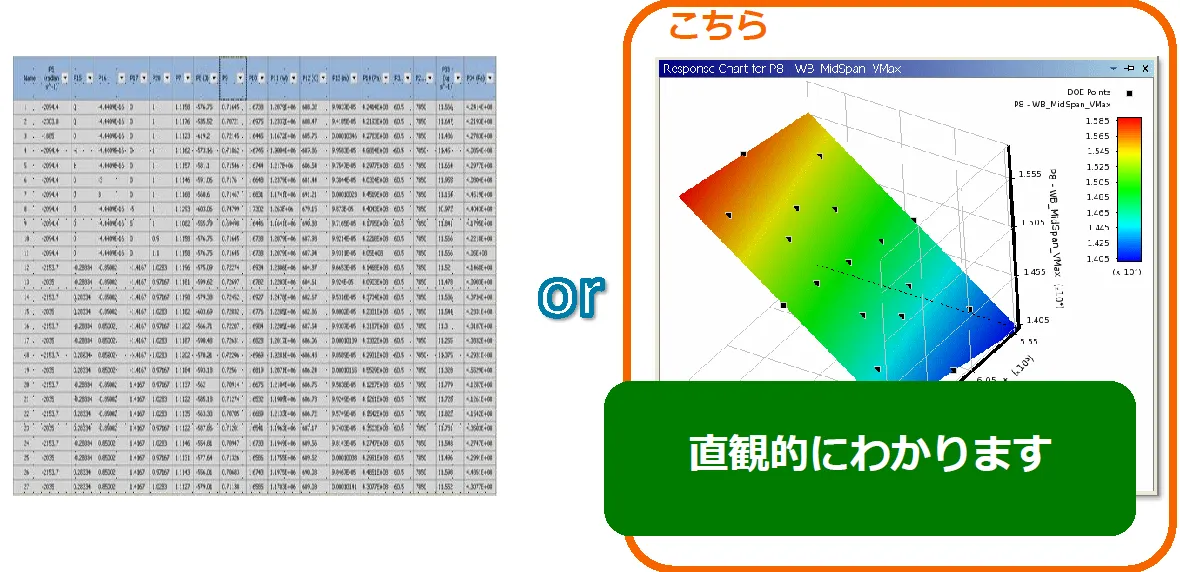
また、相関散布図においても相関性がありそうな組み合わせが一目でわかります。
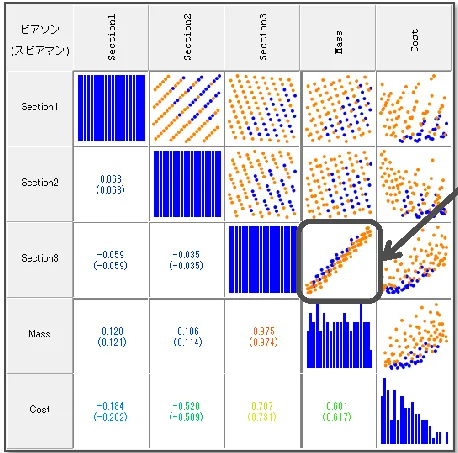
情報を直感的に理解するためには、さまざまなグラフや形式で可視化することは大変重要です。
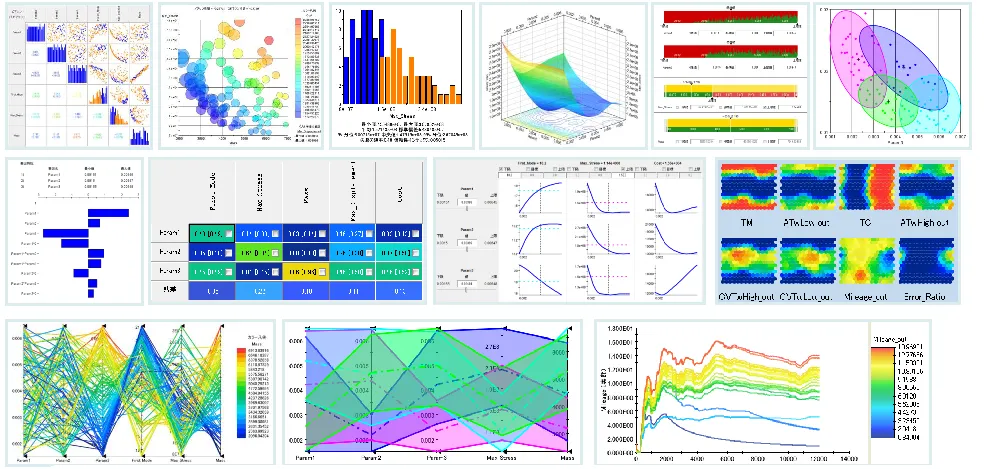
複雑化する製品設計への対応、属人制の排除
「激化する競合他社との製品競争において、高品質かつ高性能な製品を最小限のコストで生産する」というニーズは年々高まっています。また、そのような高度な解析ができるのは一部の熟練者に限られており、会社全体を通した画一性のある開発ができていないという声もよく耳にします。
最適化ツールを使用することで、熟練者頼みであった複雑な解析設定をツール上で実施することが可能になり、標準的な解析フローとして定着させることが可能になります。
ものづくりの「地図」を作るための最適化アルゴリズム
ここからは「最適化」を実現するための各手法やアルゴリズムの詳細について説明します。
実験計画法(Design of Experiments:DOE)
実験計画法とは、設計空間を分析するために、効率のよい実験配置を計画するサンプリング手法です。少ない実験(シミュレーション)回数から精度の良い結果の情報を、効率良く取り出すことができます。
応答曲面法(Response Surface Method:RSM)
実験データなどから近似式を作成する手法です。
詳細な設計空間の分析や、実験またはシミュレーションの代替に利用されます。
単目的最適化(Single Objective Optimization)
単目的最適化とは単一の目的関数を最適化する手法です。単目的最適化の場合、局所的最適化と大域的最適化の2つに大きく分けることができます。
多目的最適化(Multi Objective Optimization)
多目的最適化とは競合する複数の目的関数を同時に最適化する手法です。
トレードオフの関係にある複数の目的関数を同時に最適化し、パレート最適解を求めます。この中から意図した設計に近いものを選択します。
(例)
コスト vs. 性能
重量 vs. 強度
リスク vs. 収益
ロバスト性・信頼性解析 (Robustness/Reliability analysis)
実際の設計や製造上の不確定要因(バラツキ)を考慮して、製品の安定性や信頼性の向上を実現するための手法です。
タグチメソッド (品質工学) (Quality Engineering)
品質工学(タグチメソッド)は田口玄一博士によって考案された新技術開発・新製品開発を効率的に行なう手法です。
データマイニング (Data Mining)
データマイニングとは、一般的には統計学やパターン認識、人工知能といったさまざまなデータ解析技法を、膨大なデータに対して網羅的に適用することによって、目的に合った知識を抽出する技術を指します。データマイニングの目的は、マイニングという言葉の通りデータから意思決定に役立つ発見や洞察を導き出すことです。
CAE 最適化をはじめよう
以上が最適化を実現するための主な手法やアルゴリズムになります。CAE の最適化について少しは理解が深まったでしょうか? もっと学びたいという方には、独学で最適化についてさらに深く学ぶためのコンテンツをご用意しております。
動画コンテンツ「はじめての最適化」
本セミナーは
「CAEを活用した最適化に興味はあるが何から始めて良いかわからない」
「最適化について1から学びたい」
とお考えの設計/開発者の方向けに作成いたしました。各用語の定義のほか、最適化すると嬉しいことなどをさらに詳しく紹介しております。
「はじめての最適化」にてご紹介する内容
1部 : 最適化とは 21分
最適化に関する基本用語や一般的な最適化アプローチとは
2部 :最適化の分類 10分
定義した最適化問題の特性による分類
3部 :最適化アルゴリズム 24分
最適化計算で使用される代表的な手法や用語
4部 :実験計画法 13分
扱う問題の特性を把握するためのサンプリング手法である実験計画法とは
5部 :応答曲面法 12分
扱う問題の特性を把握するための分析手法である応答曲面法とは
6部 :ロバスト性・信頼性設計 14分
現実の設計で起こりうるバラツキを考慮するための手法とは
CAE ツールごとの最適化事例
既にご利用中の CAE ツールがある場合はツールごとの最適化事例についても公開しております。解析分野や業種ごとの絞り込みのほか、キーワード検索も可能です。PDFにてダウンロードいただけますので、是非ご活用ください。