ロバスト性・信頼性解析(Robustness/Reliability analysis)

ロバスト性・信頼性解析とは？

まずは、ロバスト性・信頼性解析についての概要を紹介します。

信頼性とロバスト性の向上

製品設計においてCAEなどのシミュレーションツール上で理論計算を行うと、同じ入力値であれば必ず同じ出力が得られます。しかし、実際の製造現場では、製造上のさまざまなバラツキ要因があるため、全く同じ製品を作ることはできません。

この製造バラツキを考慮せずに設計を行っていると、制約条件ぎりぎりの設計を行ってしまい、バラツキが発生することで不良品が量産されてしまうリスクが生じます。そこで、バラツキを考慮して設計を行い、不良品の発生を回避するために使われるのがロバスト性・信頼性解析です。

なお、ロバスト性と信頼性解析は、重視する内容に違いがあります。ロバスト性解析はバラツキの要因となる入力に対してバラツキ分布を定義し、応答のバラツキを可能な限り小さくしようという解析手法です。一方、信頼性解析は性能のばらつき分布によって失敗する確率を評価し、その失敗を無くすような設計点を探す手法となります。

初期設計からロバスト性・信頼性解析へ

それでは、ロバスト性の高い設計を実現するにはどうすれば良いのでしょうか？以下に、ロバスト性・信頼性解析の具体的なアプローチを示します。例えば、次の図の設計条件を考えてください。

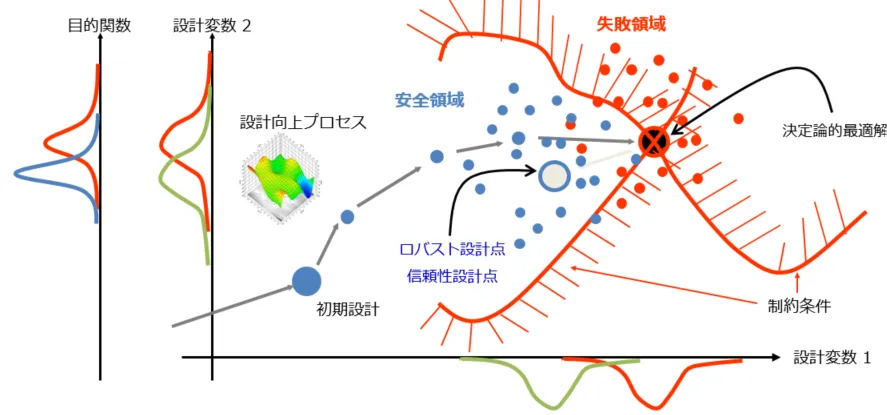
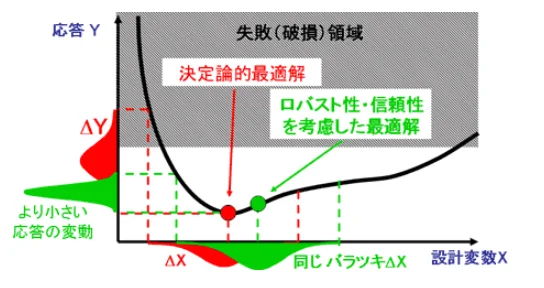
図1：決定論的最適解とロバスト・信頼性解析による解の違い

図の横軸は1つ目の設計変数、縦軸は2つ目の設計変数ならびに目的関数を示しています。また、赤い線の領域は制約条件であり、制約条件を超えると失敗領域、つまり不良品になることを示しています。

ここで、ロバスト性を考慮せずに最適設計を行うと、図の決定論的最適解が導き出されます。この解は目的関数の数値が最もよくなる点ですが、制約条件に接しているため、バラツキが発生すると高い確率で不良品が生じます。

それに対してロバスト・信頼性解析を行うと、グレーの点で示される解が得られます。この解は決定論的最適解よりは不完全ですが、バラツキがあっても失敗領域を超えず、不良品を防ぐ設計となります。

ロバスト性の評価手法

続いて、ロバスト性・信頼性解析における主要な評価手法であるモンテカルロ法、FOSM、リニアモデルモンテカルロ法について解説します。

モンテカルロ（Monte Carlo）

図2：モンテカルロ法における入出力分布のイメージ図

モンテカルロ法は、製造上のバラツキを模擬するためにランダムに入力を変化させ、多数のサンプリングを通じて出力値の標準偏差（ばらつき）を算出する方法です。

上図の横軸を入力、縦軸を出力とすると、入力に含まれるバラツキを何度も反映させた計算により、出力の分布が形成される様子が視覚化されます。なお、標準偏差の導出には以下の式を使います。

このモンテカルロ法は、そのシンプルな仕組みにより幅広い問題に適用できるメリットがあります。しかし、計算量の増加に伴い精度が向上するという特性がある一方で、計算時間が長くなるというデメリットもあります。

特に、入力値のバラツキが多い場合、精度を高めるためには大量のサンプリングデータが必要となり、計算時間が大幅に増加する問題があります。

FOSM（First Order Second Moment）

FOSMは「一次近似二次モーメント法」を意味し、一次近似を活用して計算量を減らし、標準偏差を算出する手法です。

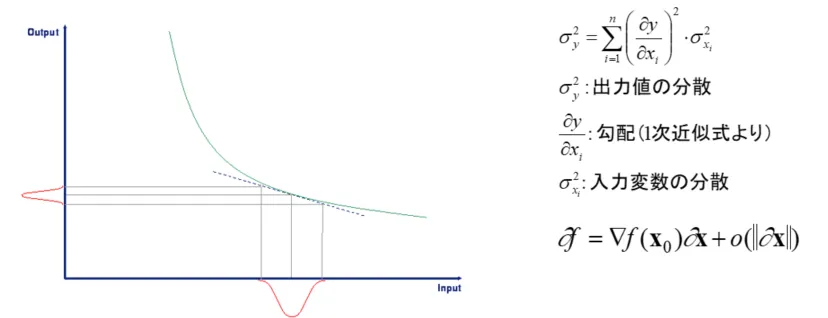
図3：FOSMのイメージ図と計算式

計算は、デフォルト値における一次近似を行い、図の点線で示される直線を求めることから始まります。その後、この直線を使用して入力値から出力を導き、標準偏差を計算します。この手法の特徴は、実際のバラツキ分布ではなく、基準値を中心とした正規分布を入力として使用する点です。

この手法により、バラツキを持つ入力パラメータに対して必要な計算量が大幅に減らすことができます。ただし、一次近似によって得られた直線が実際の応答曲線と異なるため、一定の誤差が発生するリスクがあります。

リニアモデル Monte Carlo

リニアモデルモンテカルロ法は、モンテカルロ法とFOSMの中間に位置する解析手法です。

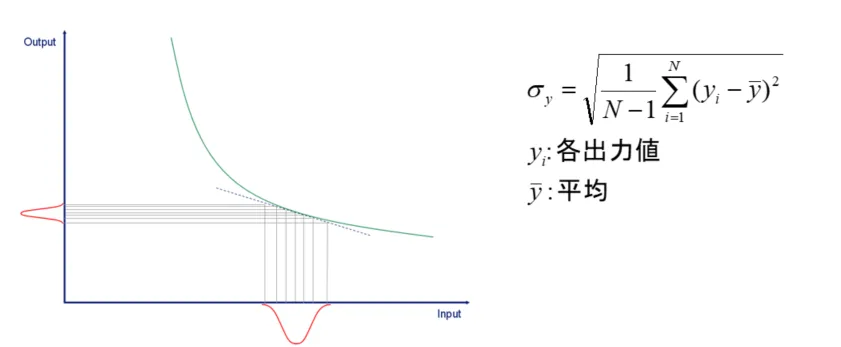
図4：リニアモデルモンテカルロ法のイメージ図と計算式

FOSMと同様にデフォルト値での一次近似を行い、目的関数の近似直線を求めます。その後、モンテカルロ法と同様に実際のバラツキ分布を入力として使用し、標準偏差を算出します。この方法は、正規分布に限定されない入力にも適用可能であり、誤差を減少させつつ、モンテカルロ法に比べて計算量を削減するメリットがあります。

信頼性の評価手法

次に、信頼性評価の主要手法であるモンテカルロシミュレーション、FORM、SORMについて説明します。

モンテカルロ

モンテカルロシミュレーションは、全てのサンプリング点に対し、失敗の割合を計算することで信頼性を評価するシンプルな方法です。

図5：モンテカルロシミュレーションの解析イメージ図

上図に示された例では、横軸U1、縦軸U2が設計変数を表し、原点が設計点、g(U)の曲線が制約条件を示します。この条件下で大量のサンプリングを行い、失敗領域のデータ量と全体のデータ量を比較することで、失敗確率を算出します。

この手法は計算量の増加に伴い精度が向上するものの、高い精度を得るためには大量のデータが必要で、計算効率が低いという欠点があります。

FORM（First Order Reliability Method）

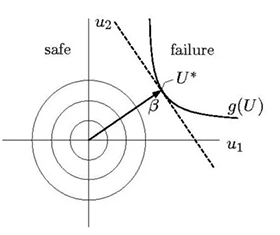
図6：FORMの解析イメージ図

FORM法では、一次近似を用いて計算量を減らし、信頼性を評価します。

モンテカルロシミュレーションの例と同じ条件下でFORMを適用すると、まず勾配法を用いて設計点から制約条件曲線までの最短距離Uを計算します。このUを求めた後、一次近似を行い、点線で示される直線を導出します。その直線は失敗領域の境界として機能し、この境界を超える確率を計算することで失敗確率を求めます。

FORMは一次近似を用いることで、計算量を大幅に削減できます。しかし、一次近似した直線と実際の制約条件曲線との間に生じるずれが、誤差を引き起こす可能性があります。一般的に、実際の制約条件は直線に近い場合が多いため、この誤差は比較的小さいです。その結果、少ない計算量で高精度な解析結果を得られることが多いのです。

しかし、制約条件が閉じた領域の場合にはFORMは適用できないなどの制限も存在します。そのため、特定の状況下でFORMを使用する際は、その適用可否を事前に検討する必要があります。

SORM（Second Order Reliability Method）

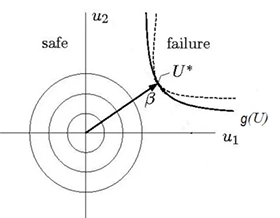
図7：SORMの解析イメージ図

SORMは、FORMの一次近似式を用いる代わりに、二次曲線を用いて計算を行う評価手法です。特に制約条件の非線形性が強い場合、SORMを使用することで誤差を低減できます。

計算の手順はFORMと同じで、設計点から制約条件までの最短距離を勾配法で導出し、二次近似による曲線を求めます。その曲線を制約条件の近似式として、失敗確率を計算することとなります。

近似式の式が変わるため、失敗曲線が二次関数に近い場合は、SORMの方がFORMより高い精度を持ちます。制約条件が閉じた領域の場合、FORMと同様SORMも適用ができません。

FORM ＋ IS , FORM ＋ ILHS

最後に紹介するのは、IS（重点サンプリング）およびILHS（ラテン超方格重点サンプリング）を組み合わせて、FORMの精度を向上させる手法です。FORMでは、制約条件に近い領域で誤差が大きくなるため、失敗領域でのサンプリングを重点的に行い、誤差を補正します。

IS（重点サンプリング）では、勾配法で求めた設計点と制約条件の最短距離のポイントを中心に、モンテカルロ法を用いたサンプリングを実施します。

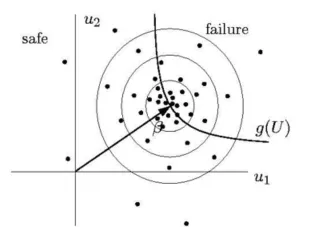
図8：FORM+ISの解析イメージ図

これにより、上図のように失敗領域近くでのサンプリングが集中し、FORMの精度を高めることが可能になります。モンテカルロシミュレーションと比較して計算量が少なくて済むため、FORMで十分な精度が得られない場合に特に効果的です。

次に、ILHS（ラテン超方格重点サンプリング）を用いた手法では、ISで用いたような勾配法による最短点を基準に、ラテン超方格法を活用したサンプリングを行います。

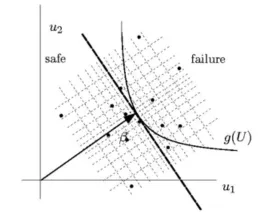
図9：FORM+ ILHSによる解析イメージ図

ラテン超方格法は、指定された範囲をグリッドで区切り、各行や列で重複しないように乱数を生成してサンプリングします。この方法により、モンテカルロ法と比べてより均一かつ偏りのないサンプリングが可能となり、ISを使用するよりも迅速に高精度な結果を得ることができます。

ロバスト性・信頼性の関連情報

最適設計支援ツール Optimus における「ロバスト性・信頼性解析」の機能について

Optimusのロバスト性・信頼性解析機能では、設計変数に多種の分布タイプを選択することができ、あらゆる不確定要因（バラツキ）を考慮したロバスト性や信頼性の評価をすることができます。

詳細はこちら▶▶

動画コンテンツ「はじめての最適化」