製品情報
ロバスト性・信頼性解析
製品の安定性や信頼性の向上を実現するロバスト性・信頼性の解析機能
一般的な最適化手法により得られた最適解は決定論的最適解と呼ばれ、最適な設計変数の組み合わせを厳密に与えた場合のみ最適な応答が保証されます。シミュレーション等においては同じ設計変数の値を何度でも与えることが可能ですが、現実の設計や製造においては様々な不確定要因(バラツキ)が存在するため、厳密に同じ設計値(寸法、物性、組立、環境条件など)を与えることは不可能です。より現実的なシミュレーションを行うには、不確定要因(バラツキ)を考慮して製品の安定性や信頼性の向上を実現する必要があります。
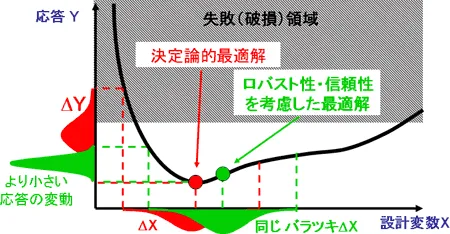
不確定要因(バラツキ)を考慮した設計案の評価
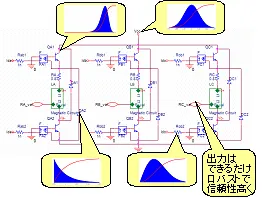
以下のような問題を抱えていませんか。
- 現在の設計案の安定性や信頼性を把握できていない
- シミュレーションによる検証では問題がないのに、試作品や量産品だと不良が多発してしまう
Optimusのロバスト性・信頼性解析機能では、設計変数に多種の分布タイプを選択することができ、あらゆる不確定要因(バラツキ)を考慮したロバスト性や信頼性の評価をすることができます。
現実的な期間内でロバスト性・信頼性の高い設計案を探索
一般的にロバスト性や信頼性を考慮する場合、多目的最適化問題となるため膨大な計算量が必要となります。そのため、短い開発期間の中でロバスト性・信頼性を評価することは現実的には難しいという問題があります。Optimusでは現実的な期間内で最適解を得るための様々なソリューションをご用意しております。
- サンプリングだけでなく、内部的に近似モデルを利用した計算効率の高いロバスト性・信頼性手法を豊富に搭載しています。
- 精度の良い応答曲面モデルを作成することにより、シミュレーションに代えて応答曲面モデルを利用することで計算時間を劇的に短縮することができます。
- 分散処理機能を併用することで計算時間を大幅に短縮することができます。
詳細については「分散処理機能」紹介ページをご参照ください。
ロバスト性の評価と最適化
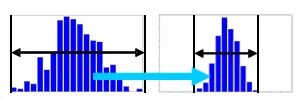
ロバスト性の向上
ロバスト性の解析機能では応答特性の分布(平均値、標準偏差)を把握することができます。最適化計算との組み合わせにより複数の応答特性の平均値と標準偏差を改善することで、よりロバスト性の高い設計を実現することができます。(同時に信頼性を考慮することも可能)
搭載手法
ロバスト性を評価する手法として一般的なモンテカルロ法のほか、内部的に応答曲面モデルを利用した手法やサンプリングをベースとしない手法により、計算効率の高い実用的な手法を搭載。
モンテカルロ法(ランダム/ラテン超方格法)
幅広い問題に適用可能
リニアモデルモンテカルロ
内部的に応答曲面モデルを利用することで高い計算効率を実現
FOSM (First Order Second Moment)
モンテカルロ法のようなサンプリングをベースとしないため、最も高い計算効率を実現
信頼性の評価と最適化
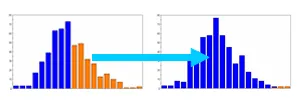
失敗確率の最小化
信頼性の解析機能では応答特性が設計の制約条件を超える失敗確率(破損確率)や制約条件までの信頼性インデックス(信頼性指標)を求めることができます。最適化計算との組み合わせにより複数の応答特性の失敗確率(破損確率)を改善することで、より信頼性の高い設計を実現することができます。(同時にロバスト性を考慮することも可能)
搭載手法
信頼性を評価する手法として一般的なモンテカルロ法のほか、内部的に応答曲面モデルを利用した手法や応答曲面モデルとサンプリングを組み合わせた手法により、計算効率の高い実用的な手法を搭載。
モンテカルロ法
幅広い問題に適用可能
FORM (First Order Reliability Method)
内部的に1次近似を利用することで高い計算効率を実現
FORM+Importance Sampling(ランダム/ラテン超方格法)
FORMとサンプリング手法を組み合わせることで高い計算効率と計算精度の両立を実現
SORM (Second Order Reliability Method)
内部的に2次近似を利用することで高い計算効率と計算精度の両立を実現
上記ロバスト性・信頼性機能によるアプローチのほか、品質工学によるロバスト設計のアプローチも可能です。
詳細については「品質工学」紹介ページをご参照ください。


