コラム用語集
データマイニング(Data Mining)
データマイニングは、膨大なデータから有益な情報を抽出する技術です。このページでは、CAE解析におけるデータマイニングのプロセスに焦点を当てて解説します。
データマイニングとは?
まずは、データマイニングの基本的な定義と、その解析プロセスの概要について説明します。
一般的な定義とプロセス
データマイニングとは、統計学、パターン認識、人工知能などのデータ解析技法を大量のデータに幅広く適用し、有用な知識を抽出する技術を指します。この技術は、まるで「採掘(マイニング)」のように、膨大なデータの中から価値ある情報を掘り出すことからその名が付けられました。
一般的なデータマイニングのプロセスとその主要な内容は、以下の通りです。
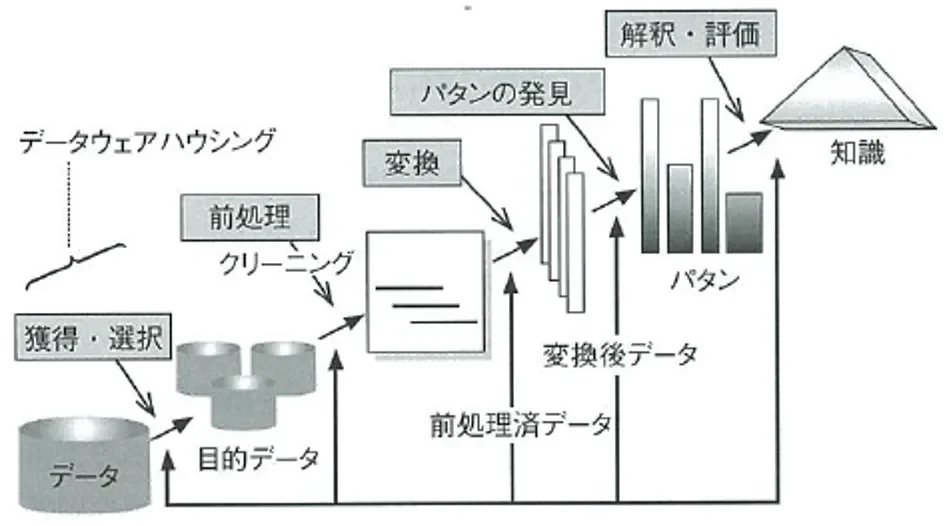
図1:一般的なデータマイニングのプロセス (引用: 「データマイニングの基礎」オーム社)
| プロセス名 | プロセスの内容 |
|---|---|
| 獲得・選択 | 用意したデータから、必要なデータを選択する |
| 前処理 | 不要なデータの除去、データ同士の結合などのデータ整理をする |
| 変換 | データの正規化、近似式による欠損値の補完などを行う |
| パターンの発見 | データが持つ傾向・パターンを発見する |
| 解釈・評価 | 発見したパターンの意味を解釈・評価し、新しい知識を得る |
CAE最適化におけるプロセス
データマイニングツール「Optimus」を使用すると、各プロセスにおける多様な機能を活用し、データマイニングを効率的に進めることができます。Optimusのプロセスごとの機能は以下の通りです。
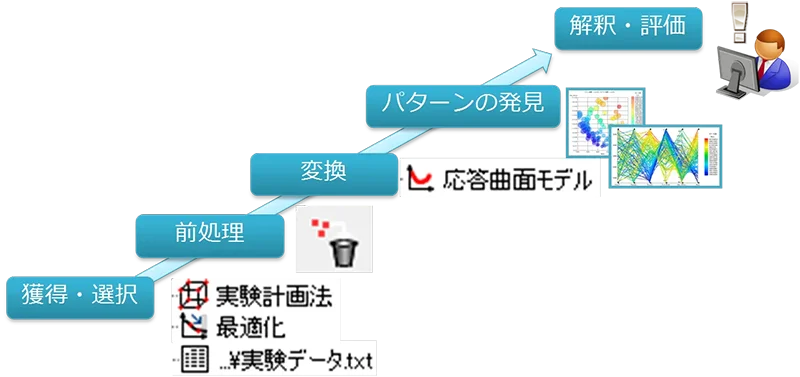
図2: Optimusのプロセスごとの機能
| プロセス名 | Optimusの機能 |
|---|---|
| 獲得・選択 | 実験計画法、最適化アルゴリズムの自動実行 |
| 前処理 | データ抽出/除去、変数選択、データ結合などのポスト処理 |
| 変換 | 正規化、応答曲面モデルの作成 |
| パターンの発見 | データ可視化、相関関係の把握、寄与度、感度の評価などのポスト処理 |
解析におけるデータマイニングの目的
先にデータマイニングのプロセスの概要をご紹介しましたが、データマイニングを行う際には、「目的を明確にする」という大前提を忘れてはなりません。
各プロセスを進めるには様々なツールが利用できますが、エンジニアが着目する設計変数や、応答、データの内容によって分析結果は大きく変わります。目的が不明瞭な場合、適切なデータやツールを選択できず、意味のある情報を得ることが困難になります。これは大事ですが見落とされがちな問題ですので、導入時には特に注意が必要です。
データマイニングのプロセス
Optimusを使用してデータマイニングのプロセスをどのように実行できるか、ここで詳しく解説します。
獲得・選択
データマイニングプロセスの最初のステップは「獲得・選択」です。以下に示すのは、Optimusに保存された様々なデータを表示する「プロジェクトツリー」です。
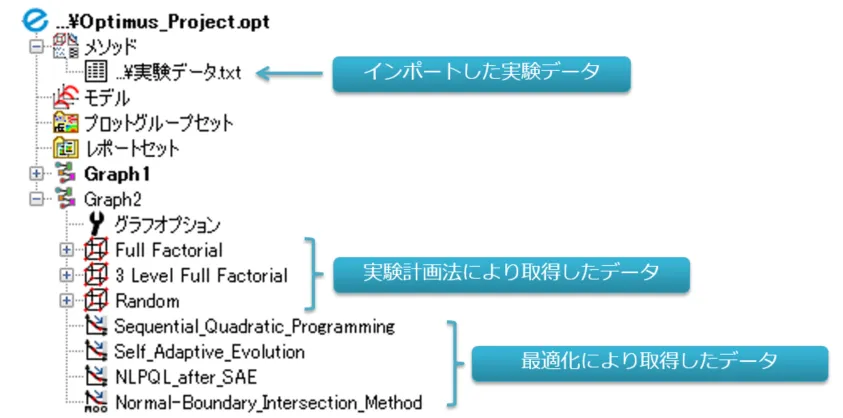
図3:Optimusのプロジェクトツリー
ここには、各種シミュレーションツールで解析した過去データ、Optimusと連携して実験計画法や最適化アルゴリズムを用いて得たデータ、あるいは事前に測定された実験結果などが含まれています。分析に必要なデータを選択して次のステップへ進みます。
獲得・選択プロセスでは、選んだデータによって分析結果が大きく変わることを理解することが重要です。例として、実験計画法と最適化アルゴリズムでサンプリングされたデータを比較します。
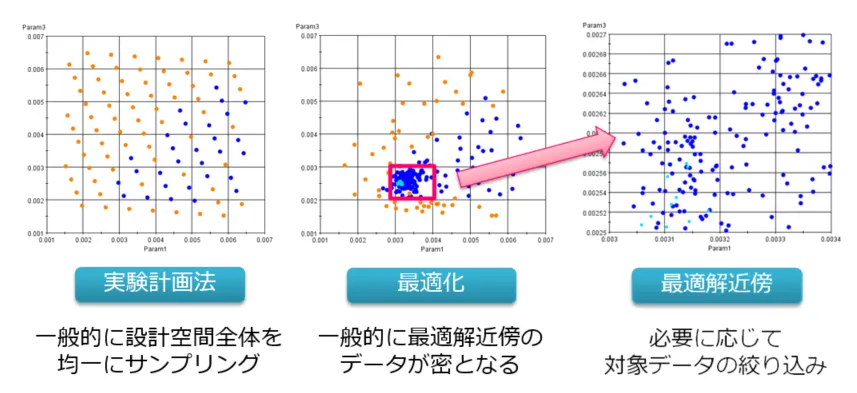
図4:実験計画法と最適化アルゴリズムのデータ比較
実験計画法は設計空間全体を均一にサンプリングするのに対し、最適化アルゴリズムでは最適解近傍のデータが密集しています。最適解近傍の傾向を分析したい場合は、最適化アルゴリズムで得られたデータを使用するのが有効です。一方、解析空間全体の傾向を理解するためには、実験計画法のデータが適しています。
このように、目的に応じて最適なデータを選択することが、データマイニングにおいては不可欠です。
前処理
データの獲得・選択が完了したら、そのデータに対して前処理を行い、データの整理・調整をしていきます。Optimusでは、データの抽出や除去、変数の選択、データの結合などのポスト処理が選択できます。
データの抽出/除去
Optimusで散布図などを表示した際、特定のデータを取り出したい場合は「データの抽出/除外」機能が有効です。例えば、最適化近傍の特徴だけを把握したい場合は、除外の機能を用いて最適化データから近傍データのみを取り出せます。
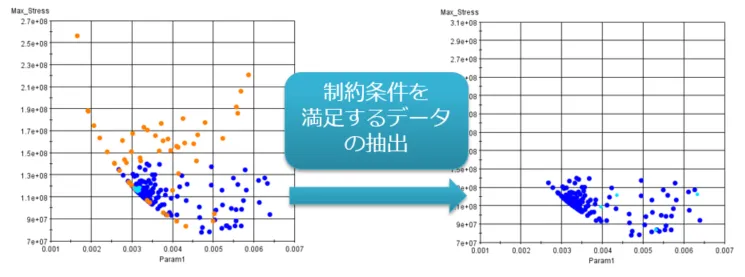
図5:Optimusによるデータの抽出
また、実現可能な設計案だけを評価したい場合は、制約条件を満たすデータのみを抽出することもできます。
データの結合
複数の実験計画法や最適化のデータなどを結合し、多くのデータを用いて分析を行いたい場合は「データの結合」機能が有効です。Optimus上では、下図のウィンドウからデータの結合が行えます。
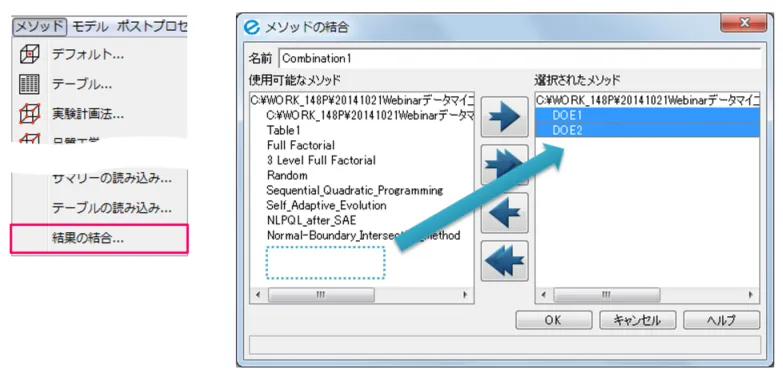
図6:「データの結合」機能のウィンドウ
ウィンドウの左側に表示されているのは、Optimusのプロジェクトツリーに保存されているデータの一覧です。この中から結合したいデータを選択し、画面右側のウィンドウに移動することで、データ同士を結合させて利用できます。
変換
前処理完了後は、「データの変換」ステップに進みます。変換プロセスでは、通常データの正規化などが行われますが、Optimusではこの作業が自動的に実施されます。そのため、ユーザーが特別な操作を行う必要はありません。なお、特筆すべき変換プロセスの一つとしては「応答曲面モデル」があります。
応答曲面モデル
応答曲面モデルは、実験計画法などで得た離散的なデータに基づいて、連続的な曲面を構築する機能を指します。この機能により、応答曲面モデルの近似式を用いてデータ間の関係を表すことができます。このプロセスの主要な利点は、可視化の際にデータの傾向を視覚的に捉えやすくなることです。
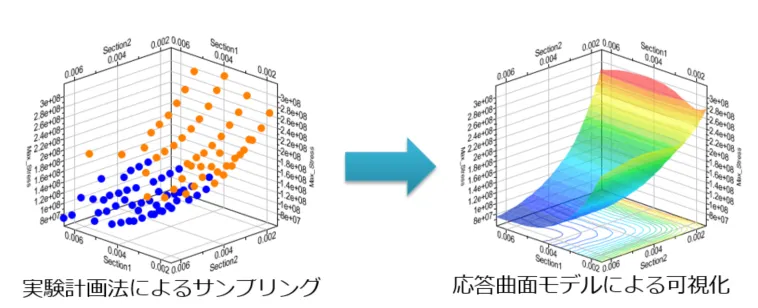
図7:応答曲面モデルの作成による可視化
パターンの発見
前処理と変換を経てデータが整った後、データマイニングの核心である「パターンの発見」に進みます。Optimusは様々なデータ解析機能を提供しており、これらを利用してデータの傾向を多角的に把握できます。ここでは、データの可視化や感度分析、相関性、クラスタリングなどの主要機能を詳しく紹介します。
データの可視化
データの可視化は、最も基本的な分析手法の一つで、文字通りデータを視覚的に表現することによって、変数間の関係や傾向を把握する方法です。Optimusには、次の表に示すように、多様な可視化手法が用意されています。
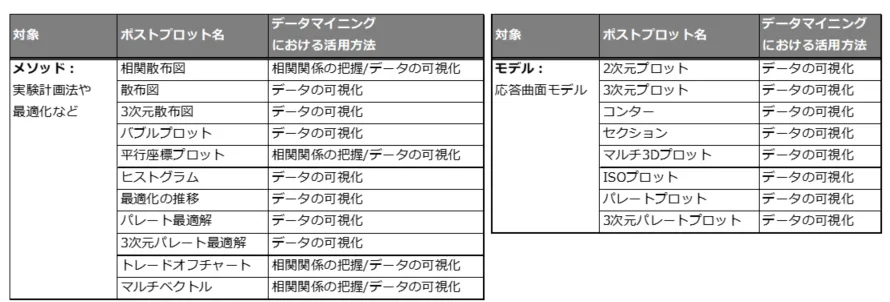
図8:Optimusの可視化手法一覧
これらの手法は、実験計画法や最適化で得られたデータのポスト処理と、応答曲面モデルのポストプロットで分かれています。そのため、分析の目的やデータの特性に応じて、適切な可視化手法を選択して使用することが重要です。
なお、可視化したデータから傾向を掴むには、グラフの形状に着目するのがポイントです。
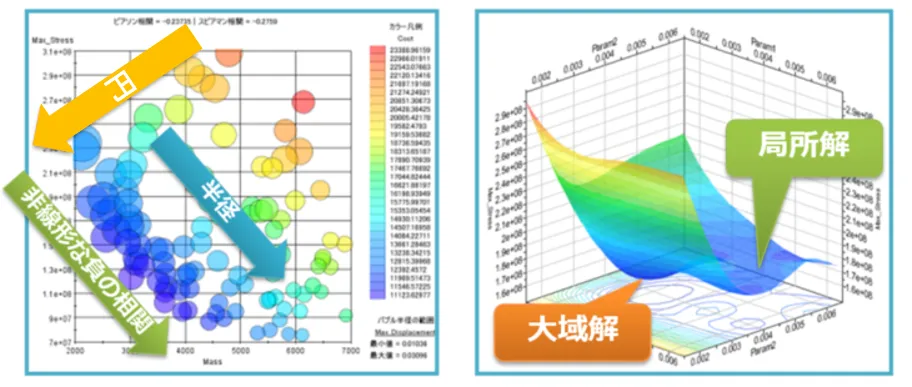
図9:可視化によるグラフの傾向
例えば、上図の左側のプロットでは、半径や円の色の連続的な変化に注目することで、変数間の関係性をより明確に捉えられます。一方、右側のグラフでは、線の形状や曲面の凹凸を観察することにより、変数間の相関性や最適解を分析できます。
さらに、特定の条件を満たすデータを可視化したい場合は、「プロットリンク」という機能が役立ちます。例えば、パレート解に関連する設計変数のデータを可視化する際に、プロットリンクを活用したグラフを以下の図に示します。
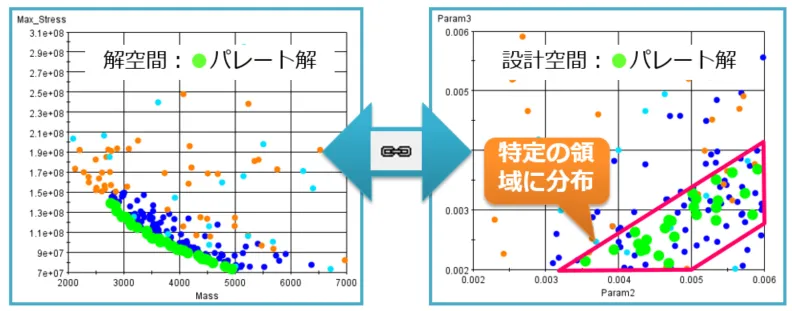
図10:プロットリンクによるパターン発見
左右のグラフはどちらも多目的最適化のデータを示していますが、左側の散布図は目的関数を縦軸と横軸に使用しているのに対し、右側の散布図では設計変数を縦軸と横軸で表示しています。右側の散布図では緑色のプロットを通じて、設計空間上にパレート解がどのような傾向で存在しているかを確認できます。
相関関係の把握
「相関関係の把握」は、変数間の相関性を把握するためのポスト処理です。Optimusでは様々なポストプロットを使うことで定量的に相関性を求めることができ、視覚的に相関性が把握できます。
例として、ポスト処理により相関関係を可視化した結果を示します。
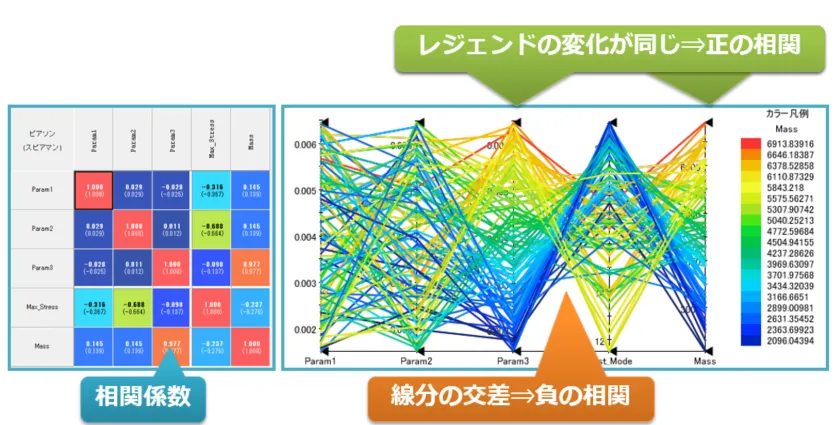
図11:ポスト処理による相関関係の可視化
左側の相関図は、定量的な相関係数を計算し、変数間の相関性を数値的に評価しています。一方、右側は平行座標プロットを示しています。この図では縦軸に各変数が配列され、各線分が個々の実験データを表しています。
このプロットにおいて、変数間の線分の関係性を観察すると、線分が交差している場合、一方の変数が小さい時に他方の変数が大きくなることから、負の相関関係が示唆されます。
さらに、このグラフでは円の色を利用して傾向を把握できます。2つの変数が同じ色の変化を示している場合、これらの変数が同様の傾向を持っていることを示し、正の相関関係があるとわかります。
寄与度、感度の評価
「寄与度・感度」は、様々な変数のパラメータが特性に及ぼす影響の大きさを測る指標です。この指標を活用することで、多数存在する設計変数の中から特に重要な変数を特定できます。Optimusでは、寄与度グラフやSOBOL分析を用いて、次に示すように寄与度を視覚化することができます。
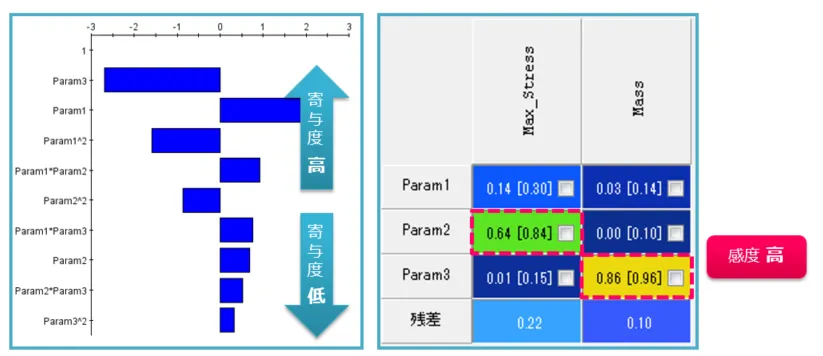
図12:寄与度・感度の可視化
左側のグラフは寄与度を示し、右側のグラフはSOBOL分析の結果です。これらのグラフを用いることで、寄与度や感度が高い変数が一目で識別でき、重要度の低い変数を最適化計算から除外することで、最適化計算の効率化が図れます。
可解領域の把握
「可解領域の把握」は、制約条件を満たす設計変数の範囲を直感的に理解するためのポスト処理です。Optimusでは「トラストリージョン」というポストプロットを用いて、下図のように範囲を視覚化できます。
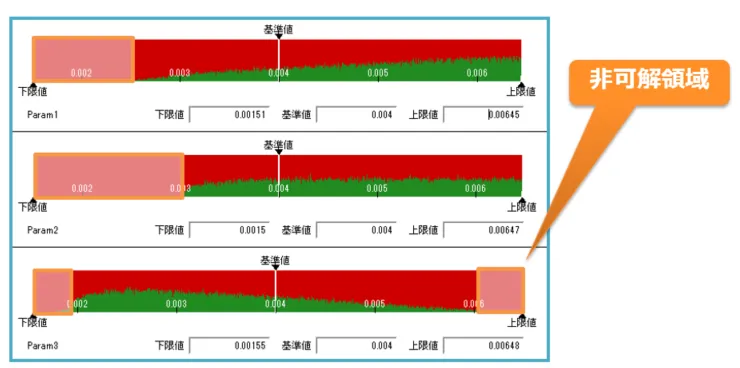
図13:トラストリージョンによる可解領域の可視化
図に示されている3本のカラーバーはそれぞれ異なる設計変数を表し、横軸は各設計変数の範囲を示します。カラーバーの中で赤い領域は制約条件を満たさない範囲を、緑色の領域は制約条件を満たす範囲を示しています。
完全に赤色の領域がある場合、その範囲の設計変数は常に制約条件を満たさないことがわかります。この情報を活用して、制約条件を満たさない設計変数の範囲を探索領域から除外することで、探索の効率を高められます。
類似度による分類
「類似度による分類」とは、特徴が似ているデータを類似度という指標を用いて分類するポスト処理です。Optimusでは、「自己組織化マップ」や「クラスタリング」といった機能を用いてこの分類を行います。なお、これらのポスト処理には変数の選択という前処理が行えます。変数によって分析結果が変わるので、類似度による分類を行う際は忘れずに設定ください。
自己組織化マップ
自己組織化マップは、教師なし学習を用いたニューラルネットワークの一形態です。このマップは、類似度の高いデータを物理的に近い領域に配置する特性を持ち、多次元データを二次元マップに投影し、視覚的に理解しやすくする効果があります。
具体的な例として、次が動物の特徴を表したデータを用いた自己組織化マップです。
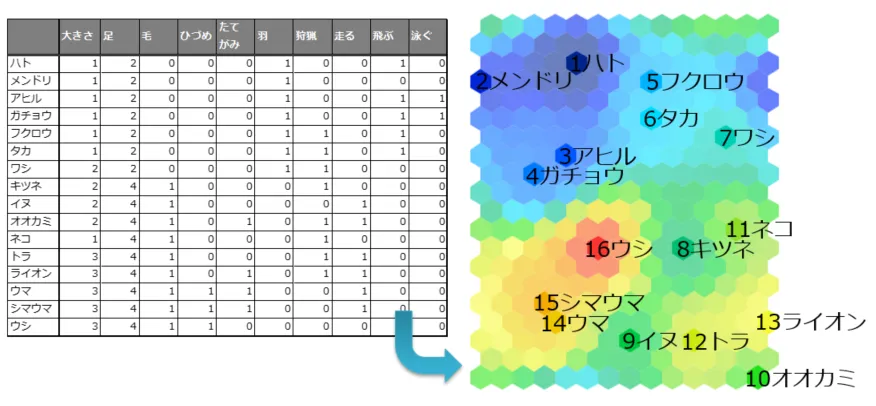
図14:(イメージ図) 動物の種類に関する自己組織化マップ
左側のグラフは、動物の種類や大きさ、足の有無、毛の有無などの特徴を表したデータを示しています。このデータを自己組織化マップに入力すると、右図のようなマップが生成されます。このマップを観察すると、青色の領域には鳥類が、緑色から黄色の領域には哺乳類が集中していることが分かります。これは特徴が似ている生物がマップ上で近くに配置されていることを示しています。例えば、アヒルとガチョウやシマウマと馬のように、外見が似ている生物はマップ上でもより近い位置に配置されています。
続いて、より工学的な応用として、ファンの形状に関する自己組織化マップの例を紹介します。
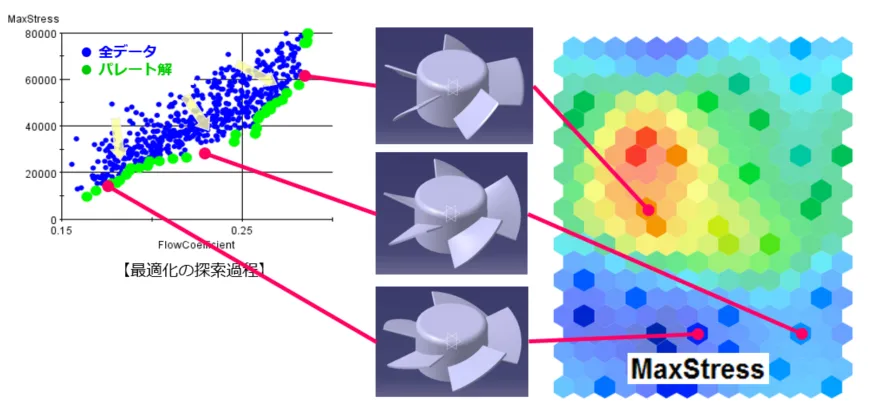
図15:ファン形状に関する自己組織化マップ
左側の散布図は、ファンの流量係数を横軸に、最大応力を縦軸にプロットしたデータを示しています。ここで、多目的最適化によって得られたパレート解が緑色のプロットとして表示されています。
右側のマップは、これらのパレート解に自己組織化マップを適用した結果です。マップ上では、最大応力の値に応じて色分けがされており、色が赤いほど応力が大きいことを示しています。また、このマップでは、ファンの羽根の傾きが小さくなるにつれて、最大応力が小さくなるという傾向が視覚的に理解しやすくなっています。
クラスタリング
「クラスタリング」とは、異なる性質を持つデータが混在する集団の中から、類似度が近いデータを集めて「クラスタ」と呼ばれるグループを形成し、分類する教師なし学習の手法の総称です。
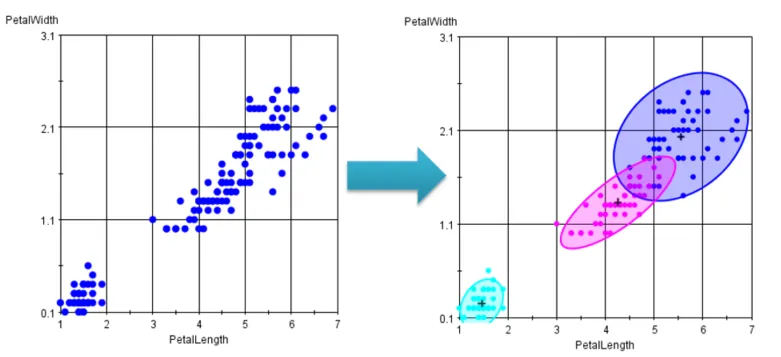
図16:クラスタリングの例
例えば、上図のデータは一見2つのグループに分かれているように見えますが、クラスタリングを適用することで、実際には3つの異なるグループに分類できることが明らかになります。このように、クラスタリングはデータをより正確に分類するための手法です。
具体的な応用例として、簡易車両モデルにおける燃費や特定の走行モードの追従性を目的関数とした多目的最適化データにクラスタリングを行った結果を示すグラフを紹介します。
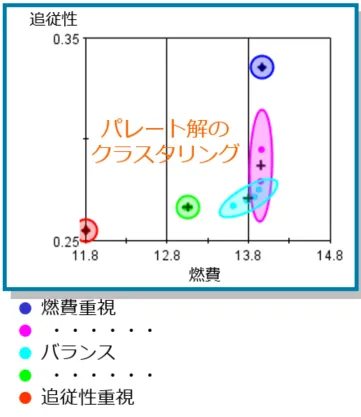
図17:簡易車両モデルにおけるクラスタリング結果
この例では、パレート解のデータにクラスタリングを適用しています。その結果、燃費を重視したグループ、追従性を重視したグループ、両者のバランスを取ったグループなど、5つのグループに分類することができました。
また、クラスタリングは、単にデータをグループ分けするだけでなく、各グループが設計変数に関して示す特定の傾向を視覚化する機能も持っています。
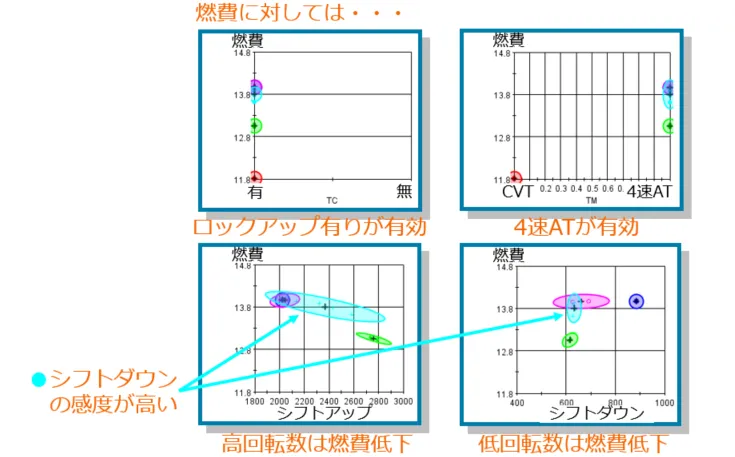
図18:簡易車両モデルにおける設計変数ごとのクラスタリング結果
上図は、さまざまな設計変数が燃費に与える影響を示しています。また、右上のグラフはトランスミッションの種類が燃費に及ぼす影響を示しています。
左下と右下のグラフは、シフトチェンジのタイミングに図17のグループを当てはめるとどのように分類できるかを示しており、設計変数による燃費への影響を分析することができます。
解釈・評価
データのパターンや傾向が明らかになった後、次のステップはそれらを解釈し評価することです。このプロセスは、対象となる現象に精通したエンジニアが担当する必要があり、自動化機能に頼ることはできません。
技術の進歩によりツールの機能が拡張される可能性はありますが、最終的な解釈はエンジニアの責任範囲内に残ると考えられます。したがって、エンジニアは適切な解釈ができるよう、継続的なトレーニングを行う必要があります。
データマイニングの関連情報
オンデマンドセミナー:データマイニングの活用
~Optimusの可視化機能による最適化データの有効活用~
~Optimusの可視化機能による最適化データの有効活用~
最適化アルゴリズムを用いた最適設計の探索は広く普及しつつありますが、複雑化する設計開発においては限定的な問題に対する最適解よりも変数間の関係性や応答への寄与度など、類似設計に活用できる知見の獲得が重要なケースがあります。本セミナーでは最適化計算などで得られたデータから様々な情報を読み取るため、Optimusの可視化機能の活用についてご紹介します。


