多目的最適化 (Multi-objective optimization)

多目的最適化の主要概念

多目的最適化において重要なのは、パレートフロンティアの把握と、それに基づく意思決定のプロセスです。この分野を理解する上で必須なのは、「パレートフロンティア」と「パレート解」の概念です。これらの用語の意味について説明します。

パレート解

パレート解とは、複数の最適解を集めた点群のことを指します。多目的最適化において、目的関数はトレードオフの関係にあるため、最適解が一意に決まることはありません。そのため、解析を行うと多数の最適解が得られます。これらの最適解を総称してパレート解と呼んでいます。

パレートフロンティア

パレートフロンティアとは、パレート解の点群をプロットしていった先に得られた曲線（曲面）のことです。無数のパレート解を導出し、それらを連続的につないだ線を意味します。パレートフロンティアが求められれば、目的関数同士の関係性が掴めます。そのため、最適化計算はパレートフロンティアを求めることが目的となります。

多目的最適化の手法

それでは、主となる多目的最適化の探索手法について解説していきましょう。手法には大まかにパレートフロンティアを求める形式と、目的関数に重みづけを行って単純化し、1つの最適値を探す形式があります。それぞれについて順番に紹介します。

パレートフロンティアを求めたのち、最終的な意思決定を行う方法

パレートフロンティアを求める代表的な手法を5つ紹介します。パレートフロンティアを求める手法について、種類ごとの原理と特徴を紹介します。

NSEA+

NSEA+は、生物の適応進化をイメージして作られた遺伝的アルゴリズムの一種です。非優越ソートによるランキング法と、混雑度トーナメントによる遺伝子操作が特徴で、あらゆる問題に対し効率的にパレートフロンティアが得られる手法として注目されています。NSEA+が具体的にイメージできるよう、アルゴリズムの流れを以下で紹介します。

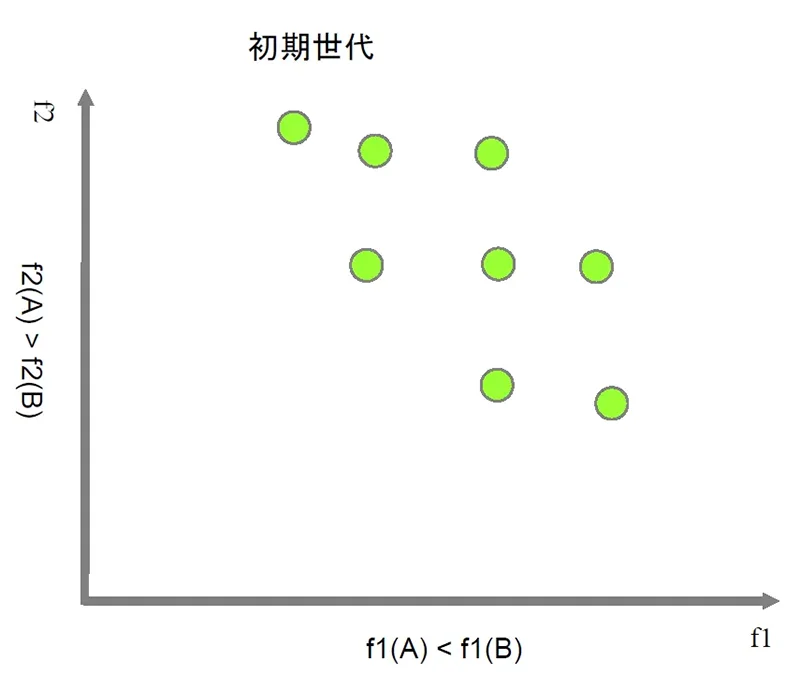
図1：初期世代の解の生成

まず、初期世代の解をランダムに生成します。その後これらの解を比較し、最も優れた解を非劣解、それ以外の解を劣解と分類します。

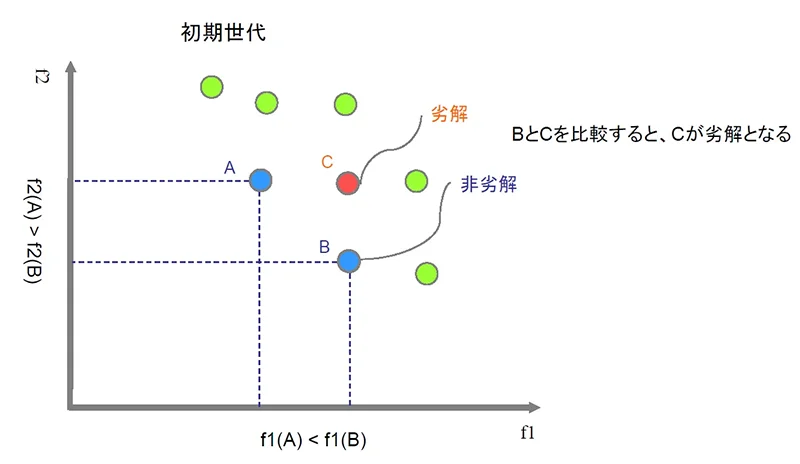
図2：非劣解・劣解の分類

同様に全ての解を分類していき、非劣解をDomination Level1、劣解を非劣解からの距離によってDomination Level2、Domination Level3に分類します。これを非優越ソートによるランキング法と呼びます。

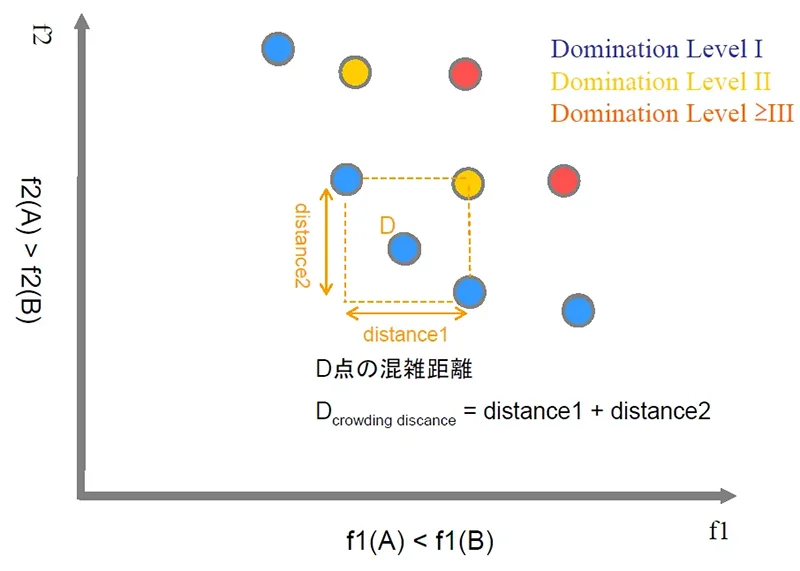
図3：非優越ソートによるランキングと混雑距離の計算

次に、分類したDomination Level1の解に対して個別に「混雑距離」を計算します。混雑距離とは、ある解の周囲にどの程度の密度で他の解が存在しているかを示す指標で、上図のD点であれば、周囲にある2つの非劣解の距離、distans1+distans2が混雑距離となります。

全ての混雑距離を計算したら、混雑度トーナメント方式により混雑距離が長い解（周囲に他の解が少ない点）をより優れた解として計算し、優れた解を親として遺伝的アルゴリズムによる新しい解を作ります。

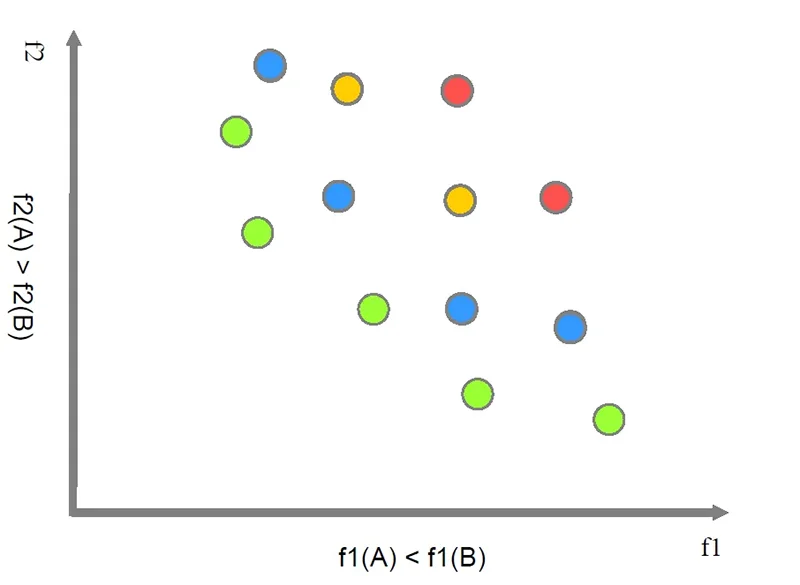
図4：遺伝的アルゴリズムによる次世代の解の生成

新しい（次世代の）解が作れたら、上記の処理を繰り返し行ってどんどん次の世代の解を作っていきます。

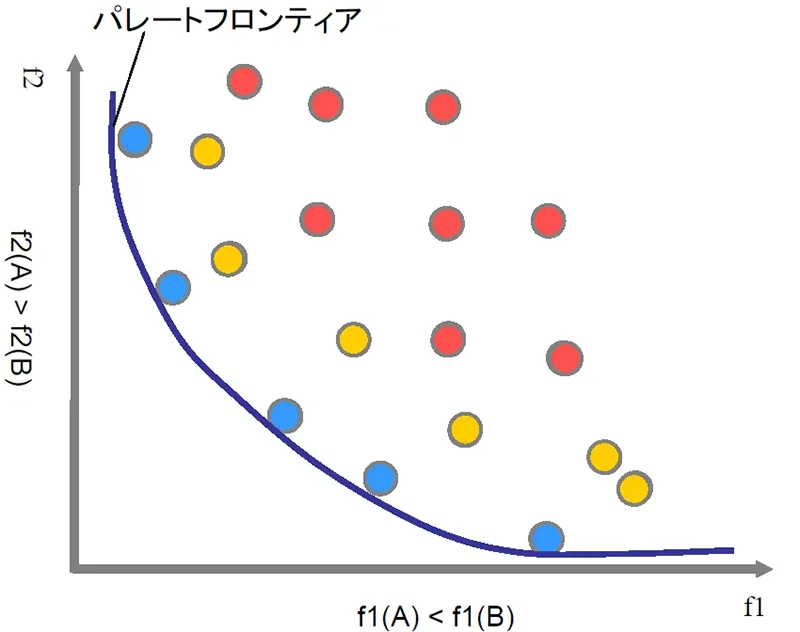
図5：解の集合によるパレートフロンティアの導出

すると、最終的にDomination Level1の集合がパレート解となり、パレートフロンティアが得られるようになります。

NBI( Normal Boundary Intersection Method )

NBI（正規境界交差法）は、局所的な最適解を得る際に有効となるシンプルな最適化手法です。2つの最適解の間にあるパレート解を均等に得ることができます。NBIのアルゴリズムの流れを以下で解説します。

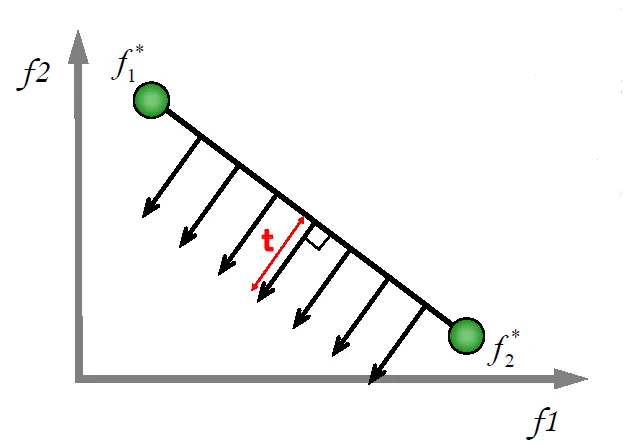
図6：NBIにおける法線の作成

まず、各目的関数に対してそれぞれの最適解を求め、それらを線（または面）で結びます。その後、求めたいパレート解の点数だけ線上に等間隔に区切り、法線を伸ばします。

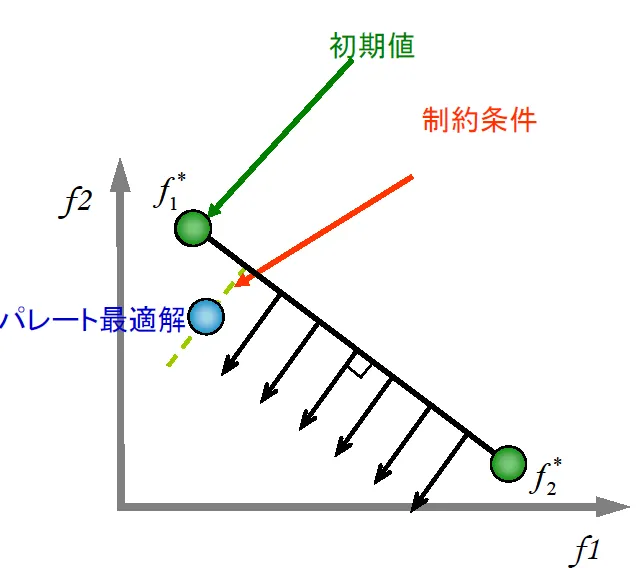
図7：最初の法線におけるパレート最適解の導出

法線を伸ばしたら、次に各法線上にあるパレート解を求めていきます。法線を制約条件、f1またはf2を初期値として逐次2次計画法（NLPQL）を用いることで、法線上のパレート解が求められます。

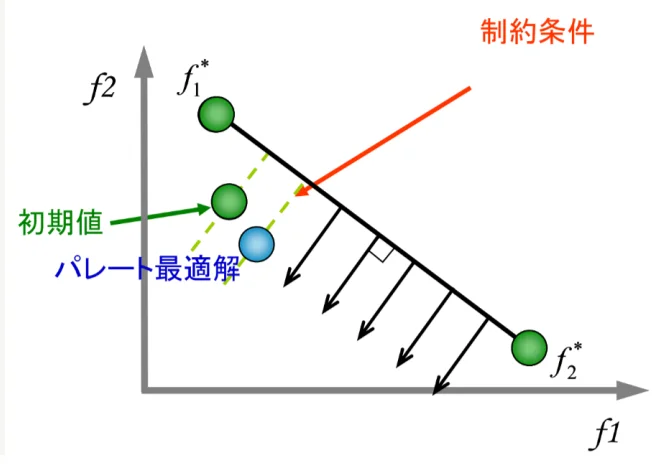
図8：2つ目の法線におけるパレート最適解の導出

次に、得られたパレート最適解を初期値として、次の法線上にあるパレート最適解を求めていきます。このように、各法線に対してNLPQLによる単一最適化計算を行うことで、局所的な多目的最適化が行えます。

mPSO

mPSOは、粒子群最適化（PSO）を多目的最適化に適用した最適化手法です。粒子群最適化は自然界で小さな鳥や魚などが群れをなして動く「群知能」をモデルに作られた手法で、単純ながら効果的に最適解を探索できる手法として注目されています。

粒子群最適化は下図のようなアルゴリズムを持ち、各粒子が位置と速度を持って計算ごとに動きながら最適解を探索していきます。

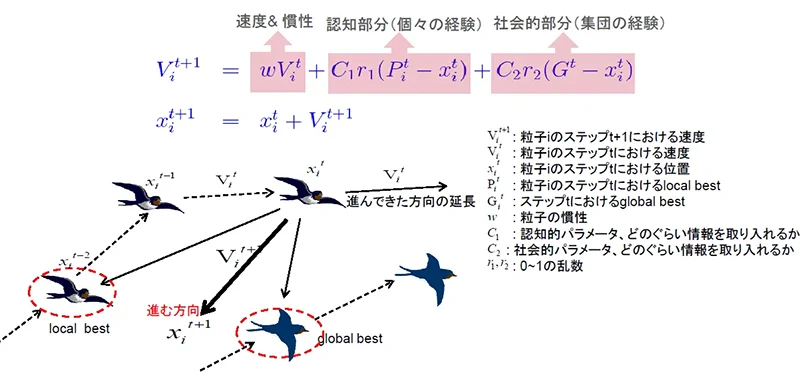
図9：粒子群最適化の解析イメージと計算式

重みづけ法

重みづけ法は、例えば目的関数1は60%、目的関数2は40%というように、各目的関数に重みづけを行うことで評価関数を作り、単目的最適化問題として最適解を見つけられるようにする手法です。重みづけを変えて何度も最適解を求めることで、下図のようにパレート解を求めていきます。

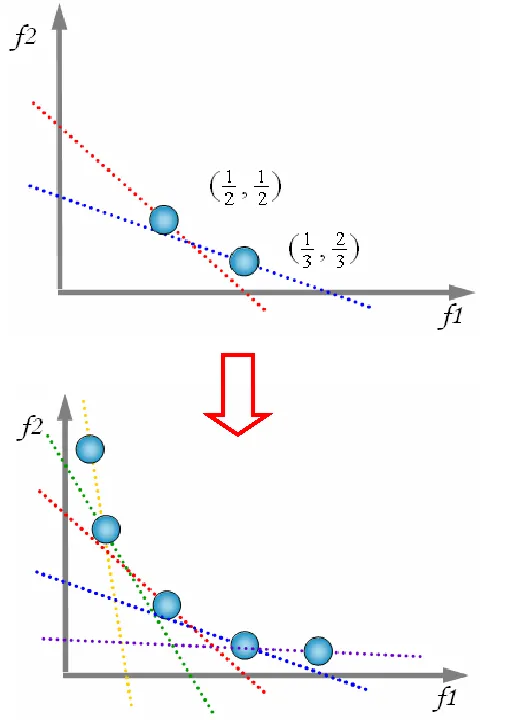
図10：重みづけ法の解析イメージ図

この手法は直観的に分かりやすく運用が簡単なので、一般に広く活用されている手法です。ただし、単目的最適化を何度も行うため計算量が膨大になりやすい上、問題によっては適切な最適解が見つけられないという欠点もあります。

Advanced eArtius Multi-Objective Optimization

Optimusに搭載されている、eArtius社が開発した多目的最適化アルゴリズムの総称です。独自の最適化技術をもとに、4つの最適化手法が選択できるようになっています。

この最適化手法では要素技術として「MGA」と「DDRSM」を用いています。

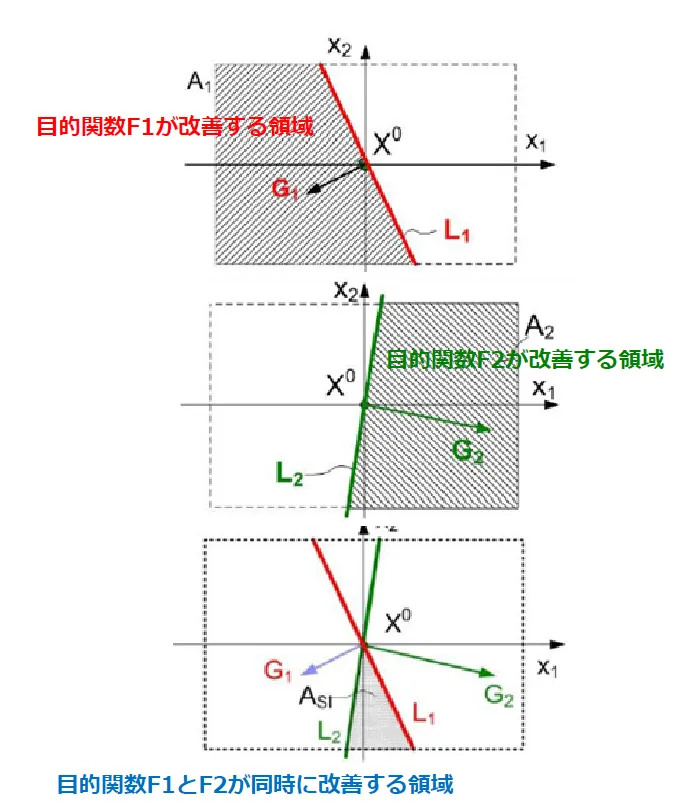
MGA（Multi Gradient Analysis）とは複数の目的関数を同時に改善できる領域（ASI）を求める手法のことです。下図のように各目的関数に着目し、改善する領域を導出することでASIを求めます。

次にDDRSM（Dynamically Dimensioned Response Surface Model）は、少ない計算量で高精度な解析が行える勾配法の一種です。

一般的によく使われる勾配法としては有限差分法がありますが、この手法は反復計算ごとに設計変数の数+1回の計算を行い、計算結果の評価を行わなければならないため計算コストが非常に高いです。

そこで、DDRSMでは最も重要な設計変数を自動的に判定して、局所的に近似式を作成、近似式に基づき、勾配を評価するという手法を取っています。
これにより、次元数に関わらず5~7回のシミュレーションで勾配を評価できるため、計算コストを大きく抑制できます。

以上の要素技術を基にして、Optimusでは「MGE」「MGP」「HMGE」「HMGP」という4つの手法を選べるようになっています。

MGEは、複数の初期値を作り、そこからDDRSMによる勾配評価を行ってパレート解を見つけていく方法です。

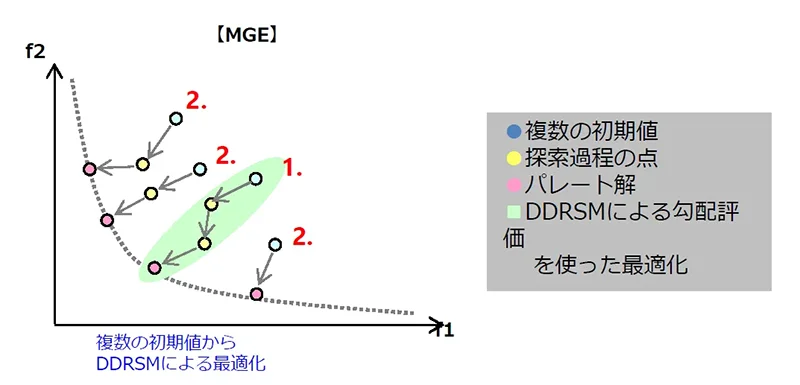
図12：MGEの解析イメージ図

上図のように初期値からパレートフロンティアに到達するまで反復計算を繰り返し、パレート解を求めていきます。なお、MGEでは計算の複雑度に合わせて初期値を1つか複数かを選ぶことができ、計算コストを調整することが可能です。

続いてMGPは、勾配法によりパレートフロンティアに沿って探索を進めていく手法です。

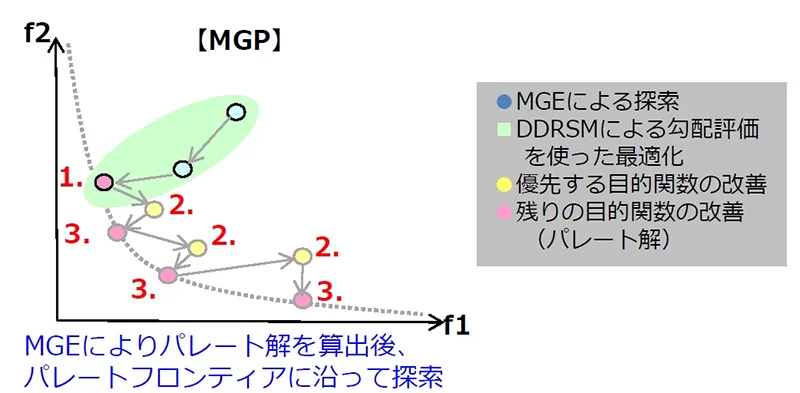
図13：MGPの解析イメージ図

初期値からMGEを用いてパレート解を求め、その後優先すべき目的関数を改善した後、再度パレート解を求めることを繰り返し、パレート解を複数見つけていきます。

次にHMGEは、MGEと遺伝的アルゴリズムを組み合わせた高度な最適化手法です。

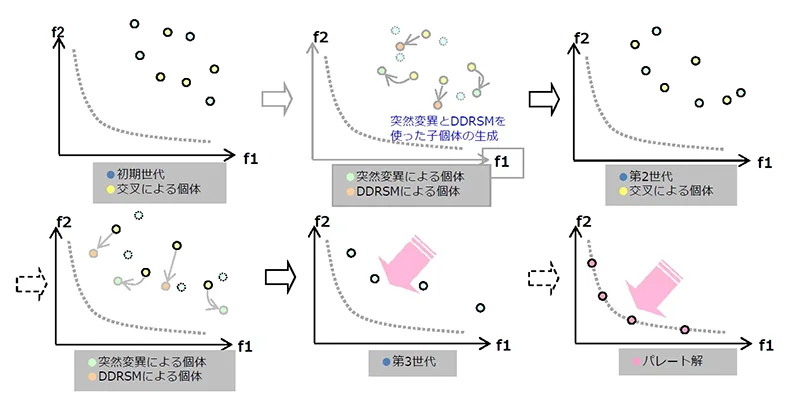
図14：HMGEの解析イメージ図

反復計算の度にDDRSMによる探索と、突然変異による子世代の生成をランダムに行い、世代を進めていく中で均一なパレート解を見つけていきます。この手法はパレートフロンティアを迅速に見つけられるため、強力なアルゴリズムとして評価されています。

最後に、HMGPはHMGEとMGPを組み合わせた最適化手法です。

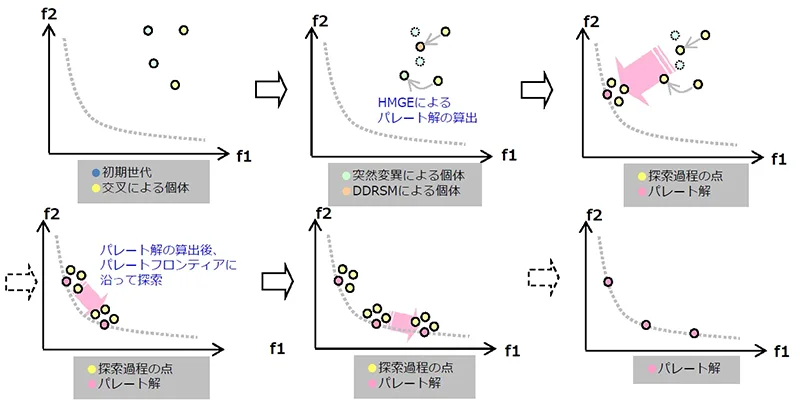
図15：HMGPの解析イメージ図

HMGEを用いてパレート解を求めた後、優先すべき目的関数を改善して再度パレート解を求めることで、パレートフロンティアを求めます。この手法は特に優先したい目的関数がある際に有効です。

予め目的関数に重みづけを行って単純化し、1つの最適値を探す形

続いては、パレートフロンティアを求めるのではなく、目的関数に優先度をつけることで1つの最適解を得る多目的最適化手法についてです。この方法には2つの種類があるため、種類ごとの原理と特徴を解説します。

トレードオフ法

トレードオフ法とは、目的関数に優先順位を決めることで、多目的最適化を単目的最適化として解析する手法です。重要度の高い1つの目的関数のみを選択し、ほかの目的関数には制限をかけて制約条件とすることで、問題を単目的最適化で解けるようにします。単一解の最適化計算となるので、NLPQLなどを用いて簡単に計算が行えるというメリットがあります。

距離関数法（ゴールプログラミング/ユークリッドノルム）

距離関数法は、理想的な最適解を仮定した上で、その最適解に近づくように解を探索するアプローチです。この方法では、最適解との「距離」を縮めることが重視されます。距離関数の次元に応じて、二つの概念が用いられます。

「ゴールプログラミング」とは、特定の目標値（ゴール）に対して解がどれだけ近づくかを最適化する手法です。この方法では、目標値と実際の解との差異を最小化することを目指します。

「ユークリッドノルム」は、複数の目的を考慮した際に、理想的な解（または目標点）と各解との間の距離を測定する手段として使用されます。各目的の達成度を成分とするベクトルを考え、そのベクトルと理想的な解を表すベクトルとの間のユークリッド距離を計算し、距離が小さいほど理想に近いとされます。

ゴールプログラミングは1次元の距離関数を用い、以下の式で評価を行います。

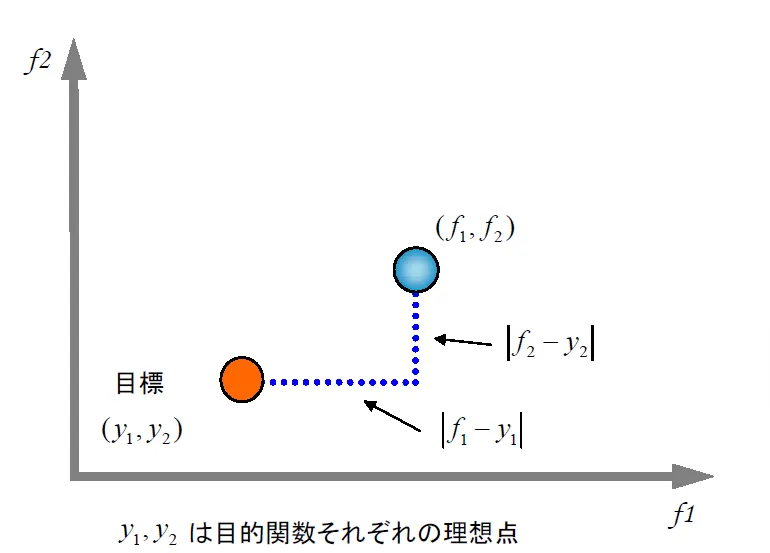
図16：ゴールプログラミングの解析イメージ図

一方、ユークリッドノルムは2次元の距離関数を用い、以下の形で評価を行います。

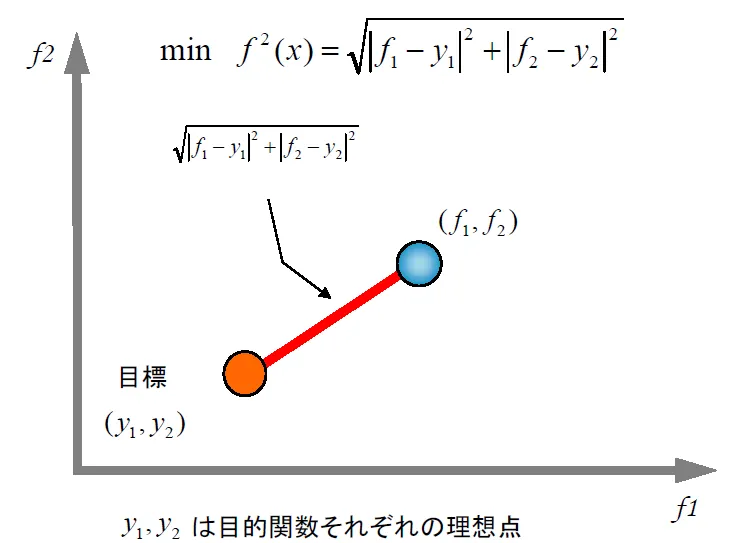
図17：ユークリッドノルムの解析イメージ図

多目的最適化の関連情報

最適設計支援ツール Optimus における「多目的最適化」の機能について

動画コンテンツ「はじめての最適化」