コラム用語集
実験計画法(Design of Experiments:DOE)とは
実験計画法とは、少ない実験(シミュレーション)回数から精度の良い結果の情報を、効率良く取り出すための実験配置が計画された手法です。
このページでは実験計画法の概要や実験計画法のさまざまな手法について紹介します。
実験計画法でできること
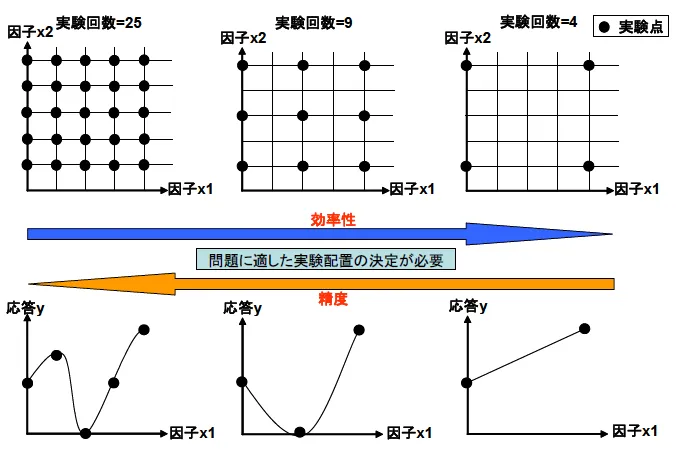
実験を行う際、実験配置の組合せと分析方法が工数と分析精度を決定します。全てのパラメータの総当りで実験を行っては多くの工数を必要とし、効率的ではありません。実験計画法により、高い精度の現象の分析を効率的に実施することが可能です。
実験計画法の基本用語
実験計画法で使用される基本的な用語について説明します。
| サンプリング | 調査対象の母集団(解空間)から標本(サンプル)を抽出すること |
|---|---|
| 因子 | 調査対象の要因(設計変数) |
| 応答 | 評価対象の出力値 |
| 水準 | 連続設計空間を離散的に扱う際の各因子の分割数 |
| 主効果 | 各因子単独の応答への直接的効果 |
| 交互作用 | 複数の因子が相互に作用しあい、特異な結果が得られる際の因子間の特性 |
| スクリーニング | 因子数が多い場合に、応答に対する寄与の小さい因子を除外し減らすこと |
実験計画法の目的
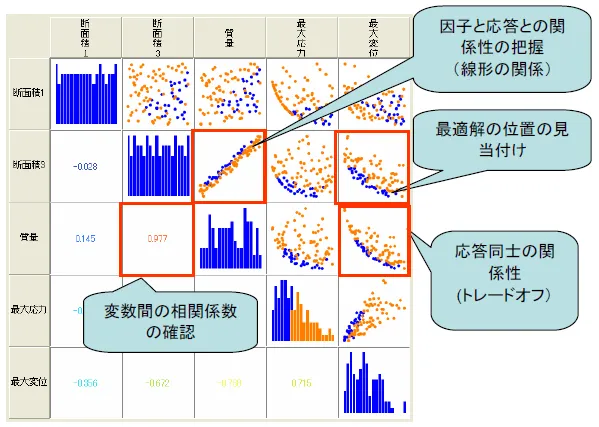
因子と応答の関係や応答同士の関係を確認・分析
応答に影響を与えている因子の把握や、因子と応答の関係や応答同士の関係を確認・分析することができます。また、実験計画法による検討の結果、最適化をおこなう前に、因子のスクリーニングや因子の範囲の絞込みにより、後の最適化において最適解探索に要する繰り返し計算回数を低減することも可能です。
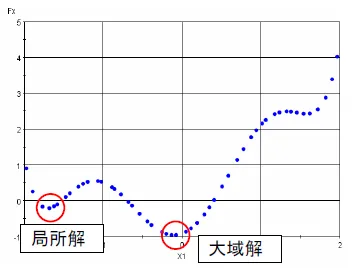
局所解や大域解の見当を付ける
最適化実施前に局所解や大域解の見当を付けることができます。また、事前に検討を付けた最適解を、局所最適化アルゴリズムの初期値に設定することで、最適解への収束までの繰り返し計算回数を低減することも可能です。
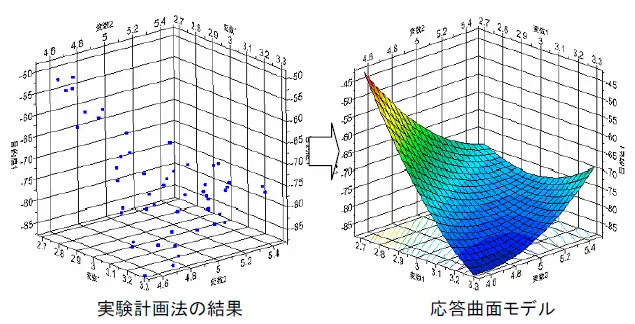
応答曲面モデル作成用のデータサンプリング
あとで応答曲面モデルを作成し、より詳細な設計空間の分析を行いたい場合、モデル作成に必要なデータサンプリングとして実験計画法を適用することもできます。
テイラー多項式の応答曲面モデルを作成する場合、必要な最低実験回数があります。
テイラー多項式の応答曲面モデルを作成するのには何点のデータが必要か?については、こちらのページをご参照ください。
実験計画法の手法
ここでは実験計画法における主な分類とそれぞれに属する手法について解説します。
2水準要因計画
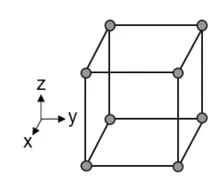
| 実験マトリックス | 設計変数の全ての2水準間の組み合わせ |
|---|---|
| 実験回数 | 2n n:設計変数の数 |
| 得られるデータ |
|
| 特徴 (注意事項) |
因子の効果、交互作用を把握でき、実験の内容が理解しやすい。因子の数が多い場合は総実験回数が膨大になる |
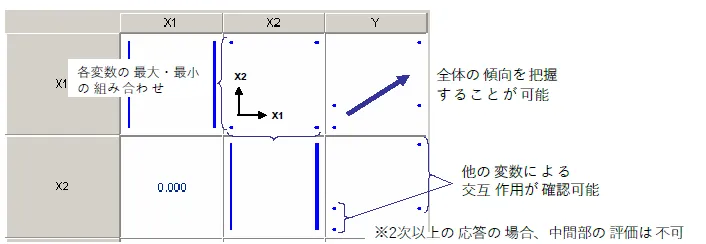
| 線形+交互作用を検出可能、2次以上の効果は評価不可 ※最小2 乗法でRSMを作成する場合はこの範囲を推奨 |
3水準要因計画
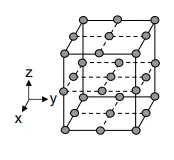
| 実験マトリックス | 設計変数の全ての3水準間の組み合わせ |
|---|---|
| 実験回数 | 3n n:設計変数の数 |
| 得られるデータ |
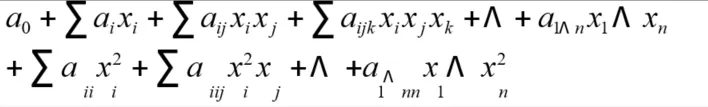 |
| 特徴 (注意事項) |
因子の効果、交互作用を把握でき、実験の内容が理解しやすい。因 子の数が多い場合は総実験回数は膨大になる |
| 1次、2次の効果や交互作用が評価可能 ※最小2乗法でRSMを作成する場合はこの範囲を推奨 |
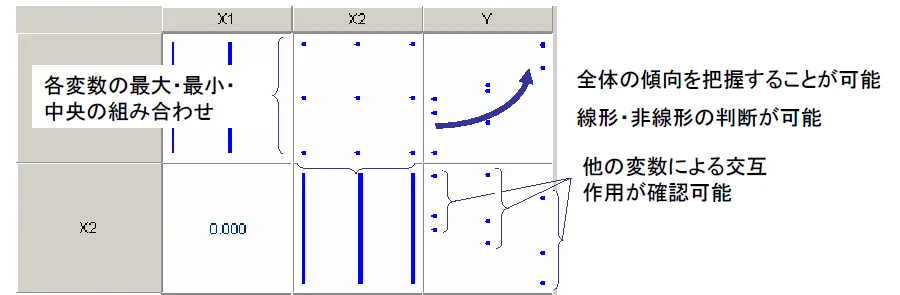
部分要因計画
| 実験マトリックス | 前述の2水準要因計画に対して、ユーザが交絡の指定を行うことが出来る実験配置(総実験回数を減らすことが可能) |
|---|---|
| 実験回数 | 実験総数は設計変数の数をn、pを交絡を定義するワードの数として2n-p |
| 得られるデータ |
|
| 特徴 (注意事項) |
・交絡により不要な実験を落とすことで、2水準要因計画よりも少ない実験回数で、線形の応答曲面に必要なデータを得ることを目的とする ・可能な設計変数の上限値は交絡のさせ方に依存する。 |
| ・交絡とは重要でない項を他の主要な項に足し込むことで省略し、実験回数を減らす手法 |
※補足(詳細は交絡をご覧ください)
P : 交絡を定義するワード
例) 設計変数X、Y、Zに対して、XYZ=I は交絡を定義するワードになり得る(P=1)
1つのワード XYZ=I から、YZ=X、ZX=Y、XY=Zの3つの交絡を得ることができる
混合水準要因計画
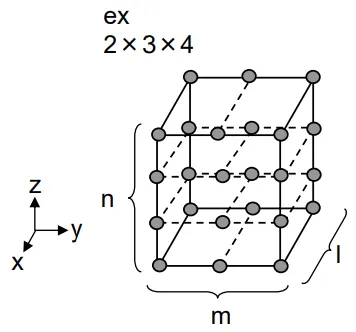
| 実験マトリックス | ・各設計変数毎に必要な実験数が異なる場合や、4つ以上の実験数を持つ 設計変数が必要な場合に使用 ・指定した全ての水準間の組み合わせ ・前述の2水準要因計画と3水準要因計画を包括 |
|---|---|
| 実験回数 | 例えば、2水準、3水準、4水準の因子の数がそれぞれn,m,lの場合: 2n*3m*4l |
| 得られるデータ | 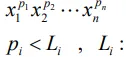 i番目の設計変数に対する実験点数 i番目の設計変数に対する実験点数 |
| 特徴 (注意事項) |
・因子の効果、交互作用を把握でき、実験の内容が理解しやすい ・因子の数が多い場合や水準数が大きい場合は総実験回数は膨大になる |
中心複合計画 (面上、面内、面外、スケール調整)
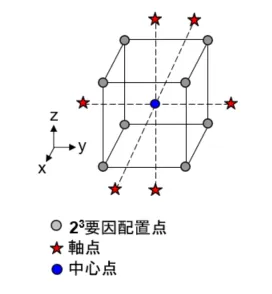
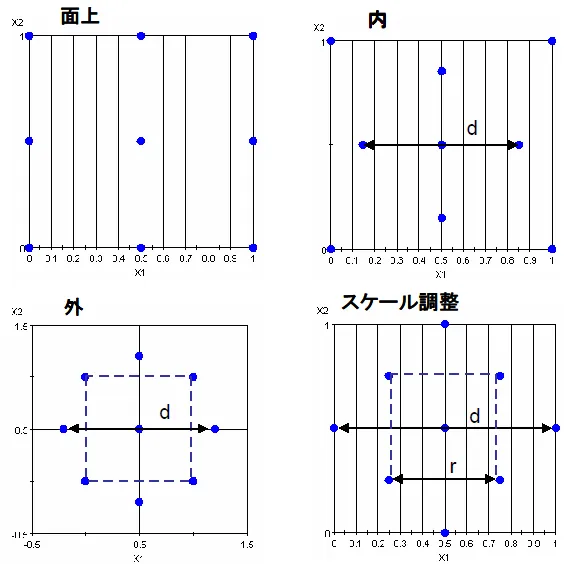
| 実験マトリックス | ・2水準要因実験に中心点や軸点を追加し、全ての因子を5水準間で評価する ・軸点が立方体に含まれるか否かで更に3つに分けられる Faced Design(面上) Inscribed design(内) Circumscribed Design( 外 ) Scaled Design (スケール調整) |
|---|---|
| 実験回数 | 2n+2n+1 n:設計変数の数、使用可能な設計変数の数の上限は13 |
| 得られるデータ |
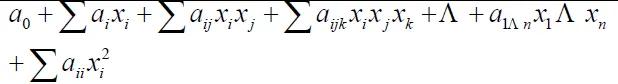 |
| 特徴 (注意事項) |
・3水準要因実験より少ない回数で実験から得られる情報も多い ・2次の応答曲面(RSM)を作成するためのサンプリング向き |
| ・3水準要因実験より著しく少ない実験回数となるが、因子の数 が増えると総実験回数は膨大になる ・因子の数が少なく一回の計算コストが低い場合にメリットがある |
プラケットバーマン計画
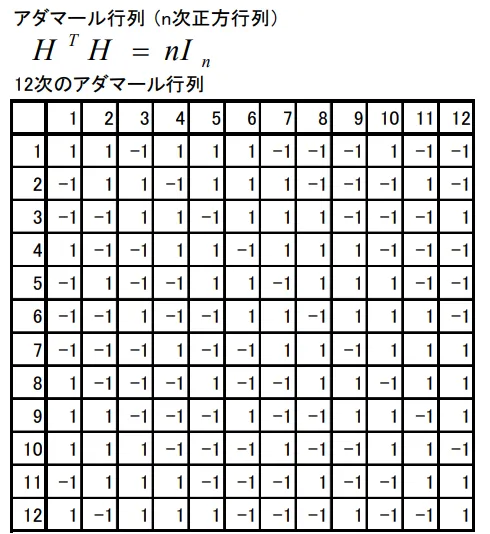
| 実験マトリックス | ・2水準要因計画に対して交絡を行った配置(アダマール行列に基づき、 主効果同士は交絡なく、主効果と交互作用間で交絡) ・実験回数を減らすための特別な配置 |
|---|---|
| 実験回数 | ・4の倍数(上限は 36回) |
| 得られるデータ |
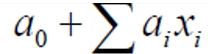 |
| 特徴 (注意事項) |
・線形効果の検出が可能 ・直交計画 |
ボックスベンゲン計画
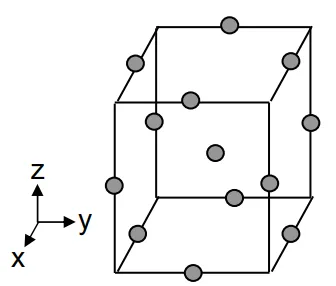
| 実験マトリックス | ・3水準要因計画から2水準要因計画の実験点と、中心複合計画の軸点(★)を取り除くことで得られる実験配置 |
|---|---|
| 実験回数 | 3n-2n-2n(n:設計変数の数) 使用可能な設計変数の数は 3~8 |
| 得られるデータ |
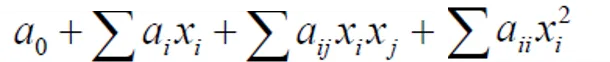 |
| 特徴 (注意事項) |
・各因子の2乗項までのデータを得ることが可能 ・設計変数同士が端点を取る実験を行わない |
直交表(品質工学)
2水準要因計画で制御因子の最大値・最小値の全通りの組み合わせ (+誤差因子)をサンプリングすると膨大なサンプリングケースが必要となります。その場合に、効率性とバランスの良い直行表を適用することで、サンプリング手法を決定します。
下記は 直交表(L4~L512)において、L4の直交表(因子数 = 3)を例としています。

– 第1列と第2列をベクトルと捉えて内積を作ります。
1×1 + 1×( -1 ) + ( -1 )×1 + ( -1 )×( -1 ) = 1 - 1 + 1 - 1 = 0 → 直交
– 第2列と第3列、第3列と第1列に関しても同じ結果となります。
1×1 + ( -1 )×( -1 ) + 1×( -1 ) + ( -1 )×1 = 1 + 1 - 1 - 1 = 0 → 直交
1×1 + ( -1 )×1 + ( -1 )×( -1 ) + 1×( -1 ) = 1 - 1 + 1 - 1 = 0 → 直交
※各列の”1”, “2”は各因子の1水準目、2水準目の値を表す
ラテン超方格法
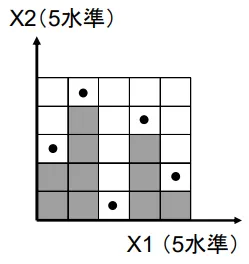
空間充填計画
空間充填計画(Space Filling)とは、設計空間内を均一にサンプリングする実験計画法の一種です。要因計画法やMaximin法を使⽤し、ユーザが指定した実験回数で設計空間の内部領域だけでなく、 設計空間の隅も、万遍なくサンプリングすることができます。

●実験点 ● 実験点がカバーする領域 ■設計空間 ⇔近傍の実験点の最小距離
設計空間を万遍なくサンプリングするための⼿法であり、下記の 2 つのアルゴリズムの技術を組み合わせています。
要因計画法 - 設計空間の隅をサンプリングする⼿法。各因子の上下限値を組み合わせたサンプリングを⾏います。
Maximin法-設計空間の中を万遍なくサンプリングする⼿法。近傍の実験点との最⼩距離を、設計空間に収まる範囲で最⼤化 することで、設計空間を均一にサンプリングする手法です。
ランダム
| 実験マトリックス | ・乱数を生成し設計変数空間にランダムに実験をばらまく実験配置 |
|---|---|
| 実験回数 | ・実験の数と乱数パターンをユーザが指定(再現性が必要な場合は 0 以外を指定、0を指定した場合は毎回異なる乱数表) ・デフォルトでは100回 |
| 特徴 (注意事項) |
・実験点の数が少ない場合、充分に一様かつ広範囲に分布しない場合があるので少ない実験点数に対しては、ラテン超方格法を推奨 |
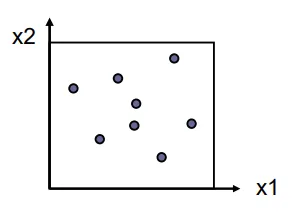
中心点・軸点・対角点
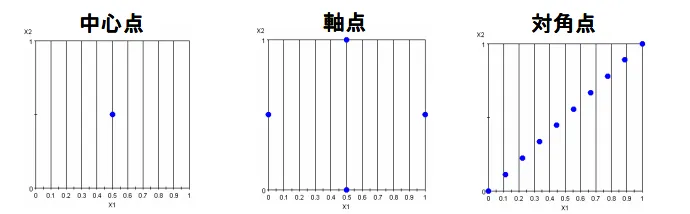
| 中心点 | ・全ての因子の平均値(デフォルト値ではない)における一回の実験 |
|---|---|
| 軸点 | ・注目する一つの因子の上下限値間で実験を行う。この際、残り因子は平均値に 固定される (単一因子計画のこと) ・全ての因子に対して繰り返す(2n回、nは因子の数) ・計算回数: 2n+1(オプション:中心点) ・設計変数の感度が評価できる ・2次的な効果や交互作用は検出不可 |
| 対角点 | ・Latine-hypercubeの対角線上の点における実験 ・実験回数はユーザが指定(デフォルトは20回) |
| ユーザ定義実験 (テーブルメソッド) (注意事項) |
・テーブルメソッドで実験マトリックスを定義することで実験が可能 ・Optimusでサポートされていない実験マトリックスを定義し実験することが可能 ・ファイルにマトリックスを定義しておくと便利 |
実験計画法の選び方
実験計画法は、因子の数、因子と応答の関係の複雑さ、1回当たりのシミュレーションの時間等を考慮し、問題に適した手法を選択する必要があります。
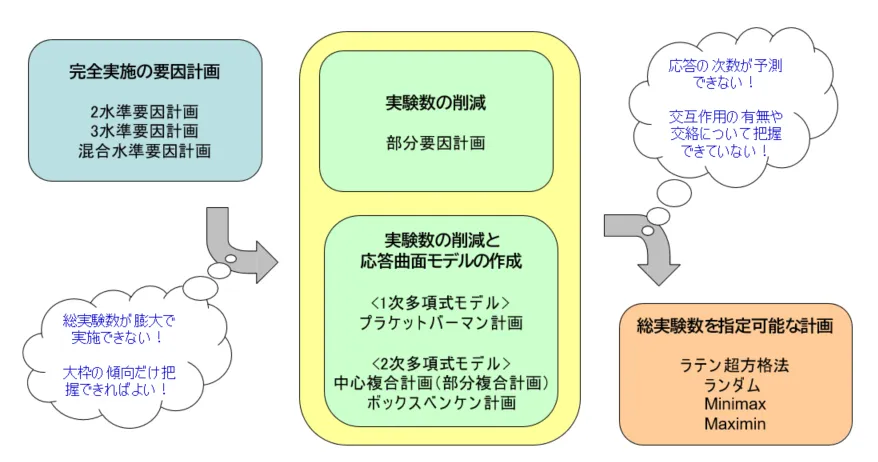
実験計画法の選択における一般的な考え方
可能な限り設計変数の全ての組み合わせを実験します。
① 完全実施の要因計画(2水準要因計画、3水準要因計画、混合水準要因計画)
を使用します。これらの計画を利用した場合、総実験数が膨大となるなど実施が困難な場合は、
② 要因計画をベースに交絡などを利用して実験数を減らした計画(部分要因計画、中心複合計画、ボックスベンケン計画、プラケットバーマン計画、直交表)
③ 総実験数を指定可能な計画(ラテン超方格法、ランダム、空間充填計画)を利用します。
②は交絡(因子の主効果と交互作用などが同一の効果として現れる)などを利用するため、選択した因子間に予め交互作用がない、あるいは交互作用が無視できる程度に小さいことがわかっている必要があります。各計画の選択は、希望の因子の水準数や組み合わせ方を考慮し、どのような交絡を利用するか(どの因子の交互作用が無視できるか)により決定します。これらが不明確な場合は、③の計画を利用します。 また、応答曲面モデルの作成を目的とした実験を行う場合は、モデル作成に適切な計画を選択します。
実験計画法の分類
完全実施の要因計画
- 2水準要因計画、3水準要因計画、混合水準要因計画
各因子に指定した水準によるすべての組み合わせにおける実験を実施する計画です。可能な限りこの計画を利用し、目的に応じた水準数を指定します。水準数の決定は、応答曲面モデルの作成を目的とした場合、因子と応答の物理的な関係性からモデルの次数を決定し、このモデルの未知係数を最小二乗法により決定するのに必要なデータ数が確保できる水準を指定します。(1次式⇒2水準、2次式⇒3水準、・・・)あるいは実験に求める精度(概略の傾向を把握⇒2水準、詳細な分析⇒多水準)により決定します。
完全実施の要因計画をベースに交絡などを利用して実験数を削減した計画
- 部分要因計画、中心複合計画、ボックスベンケン計画、プラケットバーマン計画
交絡(因子の主効果と交互作用などが同一の効果として現れる)を利用するため、選択した因子間に予め交互作用がない、あるいは交互作用が無視できる程度に小さいことがわかっている必要があります。
各計画の選択は、希望の因子の水準数や組み合わせ方を考慮し、どのような交絡を利用するか(どの因子 の交互作用が無視できるか)により決定します。
また、応答曲面モデルの作成を目的とした実験を行う場合は、作成するモデルの次数に合わせ適切な計画を選択します。(1次式⇒プラケットバーマン計画、2次式⇒中心複合計画、ボックスベンケン計画)
総実験数を指定可能な計画
-ラテン超方格法、ランダム、空間充填計画
総実験数を指定したい場合や応答の次数が予測できない、交互作用の有無や交絡について把握できていないなど、要因計画を実施できない場合に利用します。
実験計画法の関連情報
● 最適設計支援ツール Optimus における「実験計画法」の機能について
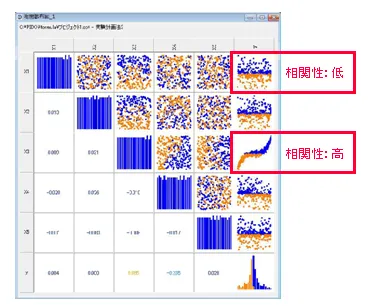
Optimusの実験計画・応答曲面手法は設計パラメータと出力の間で形成される解空間の分析に広く活用することが可能です。最適化を行う前にこれらの手法を通して多くの情報を把握することで、より「効率的な最適化」への指針が導き出されます。また、得られた結果はポスト処理を通してその相関性を視覚的に確認できます。
詳細はこちら>>
● 動画コンテンツ「はじめての最適化」
「CAEを活用した最適化に興味はあるが何から始めて良いかわからない」
「CAEの最適化を使用しているが良い最適解が得られない」とお考えの方を対象に作成した動画コンテンツです。最適化問題の特徴を分析するために実施されているサンプリング手法である実験計画法についてご紹介します。また、問題分析の必要性や、サンプリングについても解説します。
本ページは、最適化問題の特徴を分析するために実施されているサンプリング手法である実験計画法の概要や手法についてご紹介しました。CAE 解析をご検討の際は、ぜひ弊社までお気軽にご相談ください。


