コラム用語集
単目的最適化(Single Objective Optimization)
単目的最適化とは単一の目的関数を最適化する手法です。それに対し、競合する複数の目的関数を同時に最適化する手法を多目的最適化と呼びます。
このページでは、単目的最適化の概要、単目的最適化の各手法についてご紹介します。
単目的最適化の概要
ここでは、単目的の最適化問題について説明します。
最適化問題の基本用語
| 設計空間 | 設計変数値の組み合わせ集合 |
|---|---|
| 解空間 | 設計変数の組み合わせが作り出す解の集合 |
| 単峰性 | 極大値/極小値が1つ以下の解空間 |
| 多峰性 | 極大値/極小値が複数存在する解空間 |
| 勾配 | 解空間における任意の点における目的関数の導関数 |
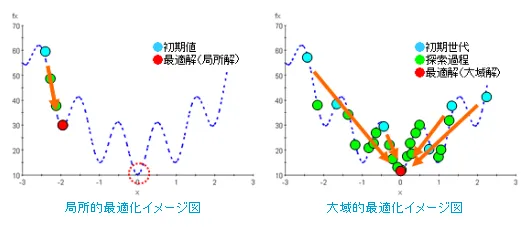
| 局所的最適解 (局所解) |
ある近傍領域における最小値/最大値 |
| 大域的最適解 (大域解) |
設計空間全体における最小値/最大値 |
最適化問題の定式化
最適化とは、ある制約条件のもとで関数などを最大化または最小化する解を探索することを意味し、一般に以下のように定式化されます。
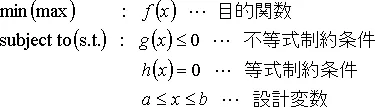
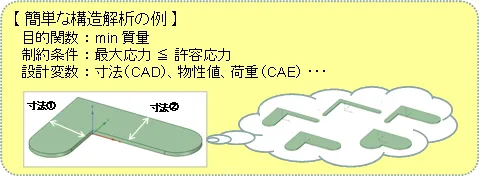
ここで、目的関数は改善したい評価項目、制約条件は必ず満足しなければならない評価項目、設計変数は目的関数や制約条件を算出するための変数です。
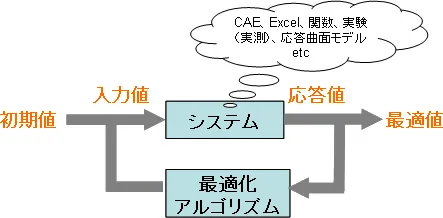
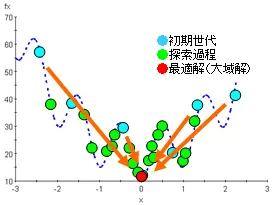
定式化された最適化問題に対して、最適化アルゴリズムは下図のように設計変数を変化させながら繰り返し計算を行い、最終的に制約条件を満足する範囲で目的関数が最小(または最大)となる設計変数を求めます。
単目的最適化の種類
単目的最適化は。局所的最適化と大域的最適化の2つに大別することができます。
局所的最適化とは
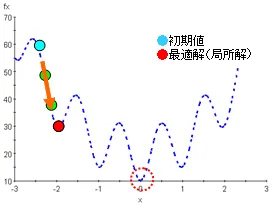
目的関数の勾配情報をもとに解を探索し、一般に解空間が単峰性となる問題に適用されます。多峰性の問題に適用した場合は、一般に初期値近傍の局所解が得られます。そのため計算コストは比較的低くなります。
大域的最適化とは
大域的最適化は一般に多峰性の問題に適用され、設計空間全体を探索することにより、高い確率で大域解を得られます。そのため計算コストが比較的多くなります。
局所的最適化、大域的最適化の各手法
ここからは局所的最適化と大域的最適化における手法の種類とそのアルゴリズムについて解説します。
局所的最適化の手法
SQP(逐次2次計画法)
SQPとは逐次2次計画法の一種です。SQP のアルゴリズムは以下の通りです。
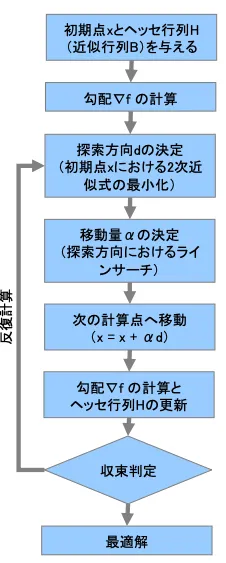
- 初期点x とヘッセ行列H(近似行列B)を与える
- 初期点x における勾配∇f を計算
- 初期点x におけるテーラーの2次近似式を求め、
- 元の問題を2次計画問題に置き換える。 この2次計画問題を解く。(準ニュートン法)
初期点x と得られた解を結んだベクトルが探索方向d となる。 - 探索方向においてラインサーチを行い、
現在よりも解が改善する点への移動量(ステップ幅)αを求める。 一般的に黄金分割法などが用いられる。
制約式のある問題ではペナルティ関数を導入した
メリット関数を最小化することで移動量(ステップ幅)αを求める。 - 得られた探索方向d と移動量(ステップ幅)αから 次の計算点 x = x + αd を求める。
- 次の計算点における勾配∇f の計算。
- ヘッセ行列Hの更新。(BFGS法)
- 収束判定(収束条件を満たせば終了。そうでなければ反復計算。)
NLPQL(逐次2次計画法)
NLPQLとは逐次2次計画法の一種です。NLPQLのアルゴリズムが SQL と異なる点は以下の通りです。
– アルゴリズムはほぼ同様
– SQPは計算精度の問題(特に勾配計算)で、目的関数や制約関数が正しく計算されず、最適化計算が終了することがある。
– この点を改善するために、ラインサーチの計算における α ( x = x + αd ) の算出方法が異なる
– 分散処理使用時にラインサーチの計算を並列処理可能
MIP(混合整数計画法)
MIPとは混合整数計画法の一種です。
設計変数に離散値を含む問題に適用でき、内部的にSQP/QP(勾配ベース)、ダイレクトサーチ(周辺探索)を利用します。 物理的に連続値が存在する設計変数(規格など)や物理的に離散値の設計変数(ギヤ歯数など)の解析に向いています。
AR(Adaptive Region)
Adaptive Regionとは、局所的最適化手法と応答曲面法に基づくハイブリッドな手法です。
探索範囲のパンニングとズーミングによるアプローチや、最適解への高い収束性、ノイズを含む問題に対する高い計算精度を実現できます。大域的最適化手法と比較して少ないシミュレーション回数で済みます。


Dakota最適化アルゴリズム群
DAKOTA (Design Analysis Kit for Optimization and Terascale Applications) は、米国サンディア国立研究所で開発された、オープンソースの最適化システムです。最適化や感度解析、信頼性解析に取り組み可能なアルゴリズム群を搭載しています。ただし、解析ツール との連携には、別途スクリプト等を作成する必要があります。また、 ポスト処理機能は搭載していません。
Optimusは、このDakotaのプラグイン機能を新たに搭載しました。 OptimusのGUIから、既存の最適化手法同様に、Dakotaの手法を利用することができます。Dakotaには多くの手法が搭載されていますが、Optimusではこの内、 13手法(単目的最適化12手法+多目的最適化1手法)がプリインストールされています。
大域的最適化の手法
NAVIRUN(Noesis Advanced adVIser)
NAVIRUNは、Noesis社が提供する新しい最適化アルゴリズム(Noesis Advanced adVIser) です。
ユーザーは、最適化アルゴリズムの知識は必要ありません。計算回数を指定するだけで最適化可能です。 従来は、最適化問題の特徴を分析し、適切な最適化アルゴリズムを選択する必要がありましたが、NAVIRUNはこのプロセスを自動的に実行するため、アルゴリズムの知識がなくても安定した最適解の探索を実現します。
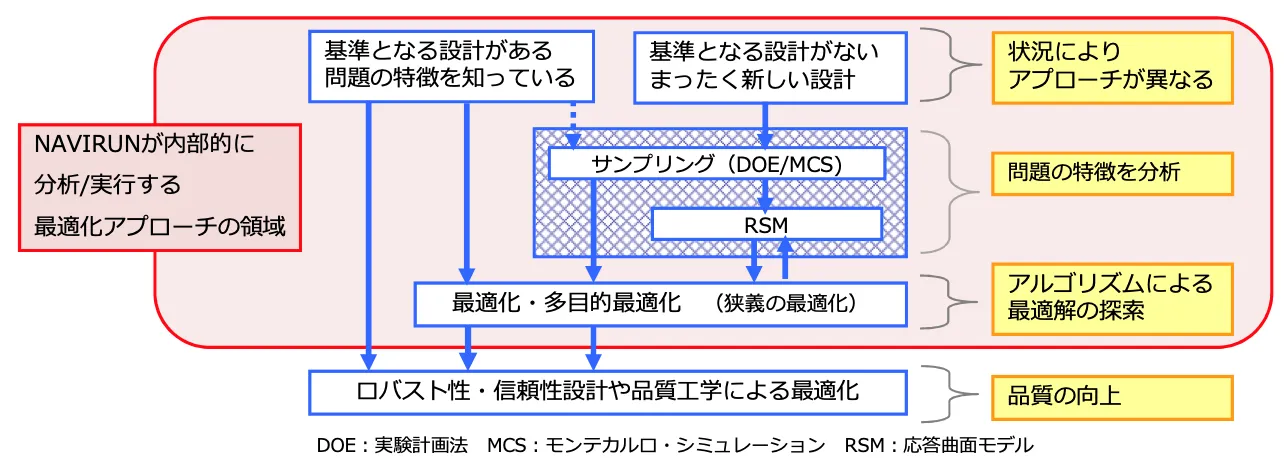
最適化の課題には下記のような点が挙げられます。
- 全ての最適化問題に万能な最適化アルゴリズムは存在しない。
- 最適化問題の特徴を把握しないとどの最適化アルゴリズムを選択すれば良いか判断できない。
- 最適化アルゴリズムが多すぎるため、どのアルゴリズムを選択すれば良いかわからない。
- 最適化に詳しくないため良い最適解が得られない。
そのような課題に対応するため、NAVIRUNは最適化問題の特徴を学習します。そして、自動的に特徴に合った最適化アルゴリズムを選択します。NAVIRUNは、オプション設定が計算回数のみであるため、最適化アルゴリズムに詳しくなくても最適化することが可能です。

SAE(Self-Adaptive Evolution)
SAEとは大域的最適化手法の一種です。SAEのアルゴリズムは以下の通りです。
- 個体数λの世代をランダムに生成
- 適合度の評価
- μ個の親個体を選出(適合度)
- λ個の個体を生成
交叉:μ個の親から性別ρの個体を使って1個体を生成
突然変異:突然変異因子αによる生成 - λ個の個体から生き残るμ個の親個体を選出
- 終了条件を満たせば終了、満たさなければステップ4へ
各個体は設計変数の情報とステップ幅の情報を持っています。
ステップ幅とは、突然変異により個体が生成される可能性がある設計空間上の範囲を指します。
DE(Differential Evolution)
Differential Evolution (DE) とは1995 R. Storn and K. Priceによって提案された手法であり、進化的アルゴリズムの1種です。大域的な最適解を高確率で求めることができる最適化手法であり、離散値の設計変数にも対応します。
一般的な遺伝的アルゴリズムとの相違点としては、アルゴリズム全体の構成は遺伝的アルゴリズムと類似している点、交叉や突然変異による次世代の生成の仕組みが異なるという2点が挙げられます。
DEのアルゴリズムは以下の通りです。
Differential Evolution (DE) のアルゴリズム
- 個体数λの世代をランダムに生成
- 適合度の評価
- 次世代の候補となる中間個体の生成 (個体数分、繰り返し)
-ランダムに異なる3個体(通常)を選択
-突然変異による個体 Vi を生成

・交叉による個体 Ti をランダムに選択した個体 Xi と Vi から生成
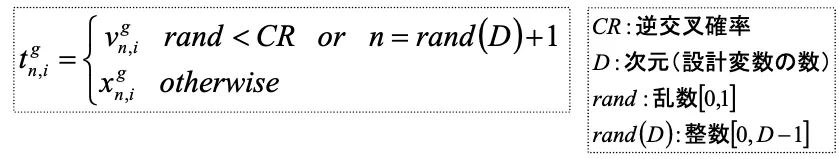
4.終了条件を満たせば終了、満たさなければステップ3へ
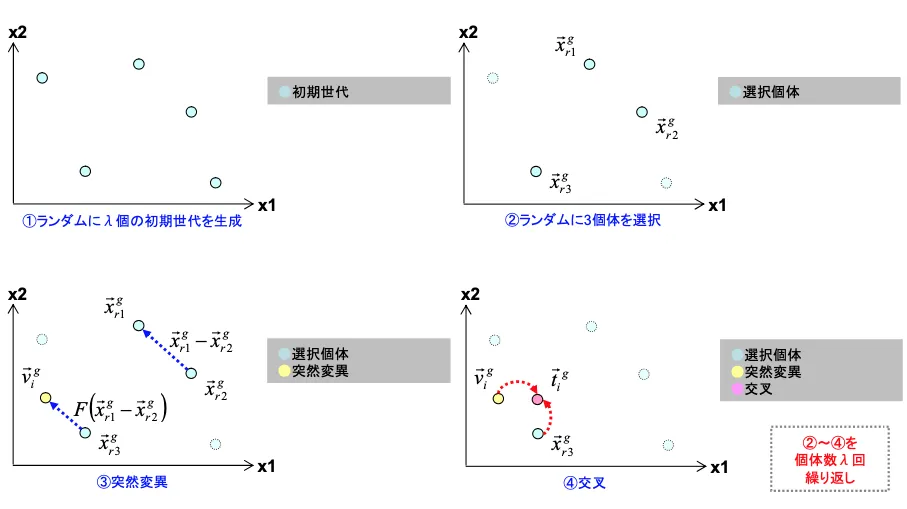
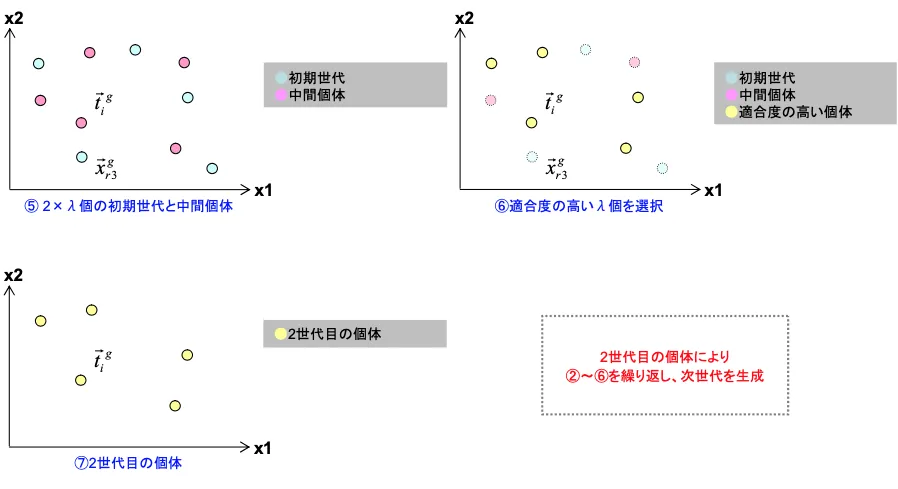
Differential Evolution (DE) のアルゴリズム(イメージ)
SAEやDEのベースとなっている基本的な遺伝的アルゴリズムについて知りたい場合は「遺伝的アルゴリズムとは」についてもご参照ください。
EGO(Efficient Global Optimization)
応答曲面モデルを利用した一般的な最適化アプローチは下記の通りです。
–実験計画法:予め決まった実験数
– 応答曲面の作成
– 応答曲面上での最適化計算(応答曲面の精度により最適解の精度が低くなる可能性がある)
– 新たに実験点を加えても自動的に応答曲面は更新されない

空間全体の精度向上が必要

一方、EGO(Efficient Global Optimization)を利用した最適化アプローチは下記のようになります。
- 反復計算毎に応答曲面を更新
- 更新された応答曲面上で最適化計算
- 最適解の情報と応答曲面の精度を利用して新たな実験点を加える

必要な部分の精度を向上させる

PSO (Particle Swarm Optimization)
Particle Swarm Optimization(以下PSO)は粒子群最適化と呼ばれ、群知能の一種です。遺伝的アルゴリズムや進化的戦略と同様に、自然の中の 動きをモデル化した発見的な手法です。
群知能(Swarm intelligence)は分散的行動と自己組織化システムを共有します。群知能は単純なエージェントの集合で構成され、ほかのエージェント や環境と局所的に相互作用します。
個々のエージェントは単純なルールに従っているだけですが、すべてのエージェントと相互作用することで、群れとして高い知能を持つような行動を引き起こします。例えば動物の群れ、ミツバチや魚群、コロニー、鳥の群れなどです。

PSOは1995年にKennedy と Eberhart によって考案されました。(1995)
各粒子(エージェント)は最適解を探索するため、各自の方向と速度により移動します。各粒子は自己の最適な位置(最適解)を保持します。(local best)
また、ほかのすべての粒子を含め、これまでの中での最良の位置を最 適解として保持します。(global best)
各粒子はそれぞれの位置を、個々のlocal bestと群全体の中で示された global bestの妥協によって調節します。
粒子群最適化については、こちらもご参照ください。
CMA-ES (Covariance Matrix Adaptation Evolution Strategy)
CMA-ES (Covariance Matrix Adaptation Evolution Strategy)とは
- 進化戦略の1種で、一般的な進化戦略と同様に突然変異、交叉により次世代のサンプル点が生成されます。
- 多変量正規分布に従った突然変異により次世代を生成し、世代を追う ごとに適応的に分布が変化します。
- オプションパラメータが少なく、設定が容易です。
- 非凸、分離不可能(設計変数間に依存関係がある)、悪スケール性、ノイズを含む、高次元などの問題に有効とされています。
- 低次元や分離可能(設計変数間に依存関係がない)な問題に対しては、勾配ベースのアルゴリズムよりも収束が遅い傾向にあります。
- 突然変異の分布形状が標準的な進化戦略と異なり、進化の過程で徐々に適応を行う共分散行列によって多変量分布が生成されます。
- 共分散行列は変数間の依存関係を表しています。
- 最適解への収束を早めるため、進化の過程で目的関数の局所的な形 状により共分散行列が更新され、突然変異が適応します。
- サンプル点の学習は、次世代の個体のランキングに従った重みだけが利用され、目的関数の値そのものや導関数は必要とされません。
- 世代ごとに個体群の分布形状が 変化しながら、少ない世代で大域 解へ収束する様子が確認できます。
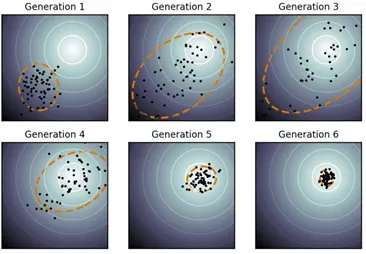
2次元の最適化問題の例
SOMBAS
SOMBAS ( SOM Based Adaptive Sampling ) とは、自己組織化マップ (SOM) をベースとした新しい適応型サンプリング/単目的最適化アルゴリズムです。
高次元(設計変数が20以上で効果を発揮)において、少ない計算回数である程度の最適解を得たい、複数の解を見つけたい、多峰性の強い解空間での解析において、有用です。
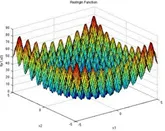
出典元:https://www.sfu.ca/~ssurjano/rastr.html

Dakota最適化アルゴリズム群
局所的最適化の手法に記載の「Dakota最適化アルゴリズム群」をご参照ください。
SAEやDEのベースとなっている基本的な遺伝的アルゴリズムについて知りたい場合は「遺伝的アルゴリズムとは」についてもご参照ください。
単目的最適化の関連情報
最適設計支援ツール Optimus における「単目的最適化」の機能について
Optimusの単目的最適化手法を使用すると設計上考慮すべき複数の制約条件を満足した上で、改善すべき目的関数(評価値)の最適解を得ることができます。考慮すべき評価値の許容範囲や優先順位が明確で、ある評価値を極限まで改善したい場合などに有効です。
詳細はこちら>>
動画コンテンツ「はじめての最適化」
「CAEを活用した最適化に興味はあるが何から始めて良いかわからない」
「CAEの最適化を使用しているが良い最適解が得られない」とお考えの方を対象に作成した動画コンテンツです。最適化とは何か?、最適化に関する基本用語、最適化計算で求める最適解とは?、といった最適化の基本となる内容についてご説明します。
本ページは、単目的最適化の概要、単目的最適化の各手法について紹介しました。CAE 解析の最適化をご検討の際は、ぜひ弊社までお気軽にご相談ください。


