コラム用語集
応答曲面法（Response Surface Method：RSM）とは
実験計画法などにより得られたサンプリング結果から、さらに有用な情報を抽出するためには、応答曲面法を用いてモデルを作成します。このページでは応答曲面法の概要や応答曲面法のさまざまな手法についてご紹介します。
応答曲面法とは
応答曲面法は、不連続なデータを連続的な曲面として近似したモデルを作成する手法です。
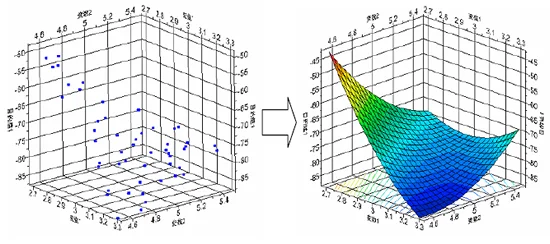
応答曲面法を利用するメリット
1. 応答の様子を視覚的に推測するのに役立つ
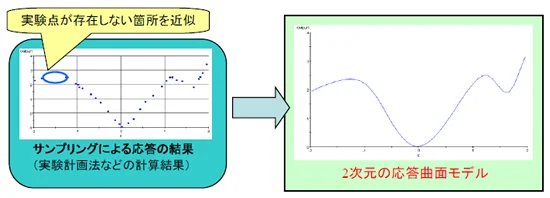
応答曲面法で作成した近似モデルは応答の様子を視覚的に推測するのに役立ちます。単なる数値データの並びに過ぎない実験結果から高度な統計解析の知識なしに設計変数間、あるいは設計変数と目的関数間の関係を見ることができます。
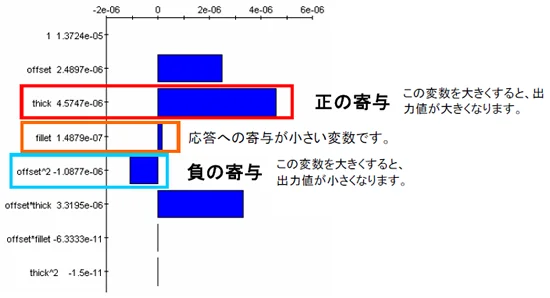
2. どの設計変数がどの程度寄与しているのか確認できる
評価したい応答に、どの設計変数がどの程度寄与しているのか確認することができます。
3. 短時間で最適解を得られる
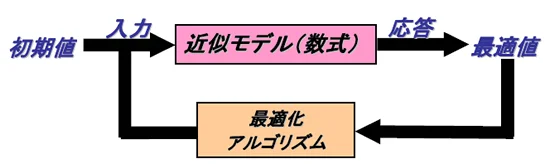
通常、最適化計算を実行すると、最適解を得るまでトライ&エラーを繰り返し、場合によっては数百回の繰り返し計算を行うことになります。シミュレーションの計算時間が数時間かかるとすると、現実的な時間内に最適解を得ることができません。
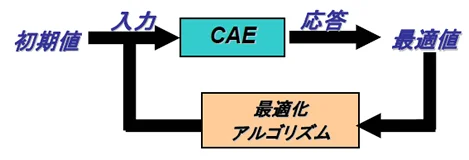
シミュレーションを応答曲面法で作成した近似モデルに置き換えると、応答は数式に設計変数を代入するだけで短時間に得ることができます。数百回繰り返し計算をしたとしても、非常に短い時間で最適解を得ることができます。
ただし、精度の良いモデルが必要になります。
応答曲面法の手法
応答曲面法はデータから近似式を作成する手法です。近似する手法は、最小二乗法と補間法に分けることができます。
最小二乗法は、誤差を含んだデータから想定される特定の関数に近似する手法で、全体の傾向を近似するときや、ノイズを含むデータに向いています。
一方、補間法は原則的に実験点を通過するような近似式を作成するため、応答が複雑な（非線形性が強い）場合に用いられる手法です。
応答曲面法にはさまざまな手法があります。ここからは応答曲面法の各手法の詳細についてご紹介します。
最小二乗法
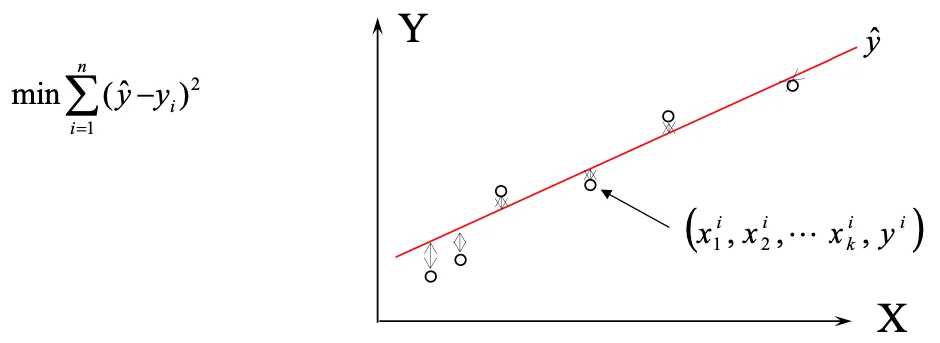
最小二乗法とは、回帰分析に使うデータ処理一種です。誤差を含んだ実験データの処理において、実データとの差分の2乗の和が最小になるよう、回帰直線を選ぶ手法を指します。
最小二乗法で近似する関数として、次の関数を利用できます。
- テイラー多項式
- ユーザー定義
- RSM
一般形式としては下記の数式を用います。
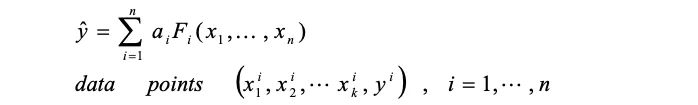
α1 はモデルの各項の係数です。実験値と近似モデルの二乗誤差が最小となるα1を求めます。
関連情報
テイラー多項式の応答曲面モデル作成に必要なデータ数について
一般に設計変数の数や次数を増やせば増やすほど、測定データとの適合度を高めることができます。しかし、ノイズなどの偶発的な変動にも無理にあわせてしまうため、他のデータには合わなくなります（過適合問題、またはOver fitting）。そこで必要な項を絞り込み予測精度の高いモデルを選択するための指標として、情報量規準を利用することができます。
赤池情報量規準（AIC：Akaike’s Information Criterion）
赤池情報量規準とは、統計モデルの尤もらしさを評価する情報量規準です。小さいほど尤もらしいモデルといえます。テイラー多項式は項の数かが増えるとノイズとなる項を含む場合があります。AICはノイズとなる項をモデル化せず、必要な項を絞り込み最も良い項の組み合わせでモデルを作成します。
指定するオプションは下記の通りです。
- 最大次数の指定(3次まで)
- 項の数を指定
- 定数項 or 定数項+線形項の選択
補間法
補間法とは、離散的な点が存在するケースにおいて、与えられた点の間を別の関数で近似する手法です。
OptimusにはRBFとKrigingが搭載されています。
放射基底関数 (RBF)
放射基底関数 (RFB) とは、原点でない、ある基準点 c からの距離(ユークリッド距離)のみに依存する関数です。
下記の式にて求められます。
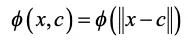
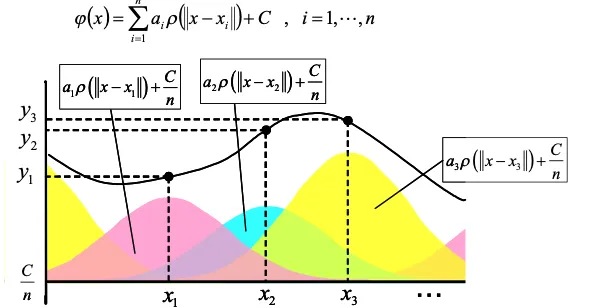
各標本点を基準点とした放射基底関数を足し合わせて近似します。
Kriging
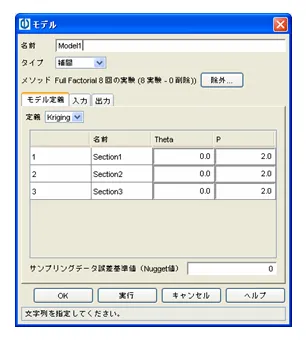
Krigingとはベイズ統計学に基づいて任意の関数分布を推定するガウス過程回帰で、非線形関数の近似に適しています。
θ : 実験点近傍からの影響度を決める 最も重要な値(θ＞0)
P : 補間の形（するどさ）を決める (1≦P≦2)
Nugget: 実験誤差を考慮する時のみ入 力(1e-12 ＜ Nugget ＜ 1e-9)
手法の背景は下記の通りです。
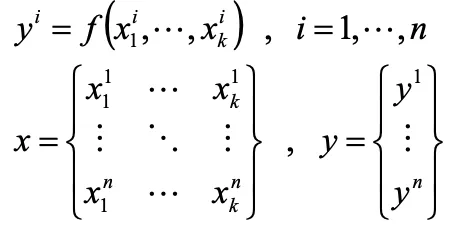
回帰により応答を実験点に一致させる場合は下記の数式になります。
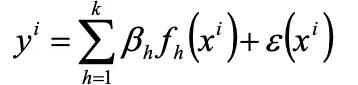
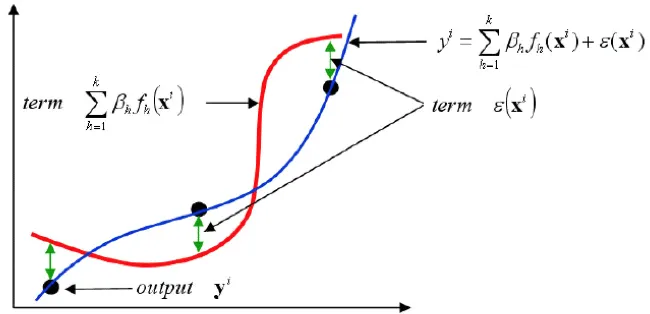
をxi の連続関数として扱え、実験点同士の距離関数として定義します。
近い位置にある実験点同士は誤差も同程度であるから誤差と距離に相関関係があると考えられ、
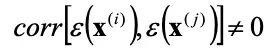
逆に遠い位置にある実験点同士では誤差と距離の相関関係はないと考えられるため、
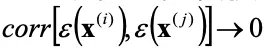
距離関数と誤差の相関関数を以下のようにおきます。
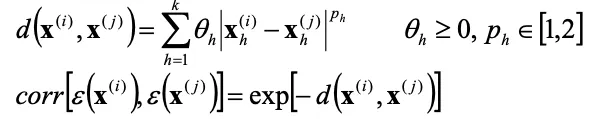
相関関数は2点間の距離が近いと高く、遠いと低い値となります。
全データの組み合わせに対する相関関数から相関行列Rを定義します。
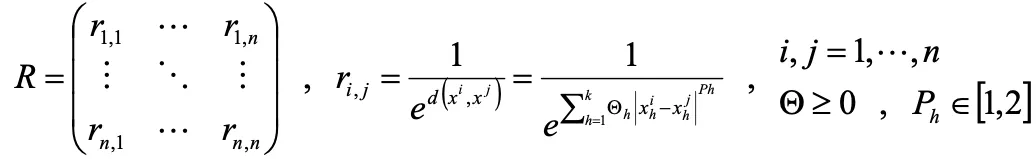
相関関数と相関行列を定義したことにより、 回帰モデルを書き換えることができます。
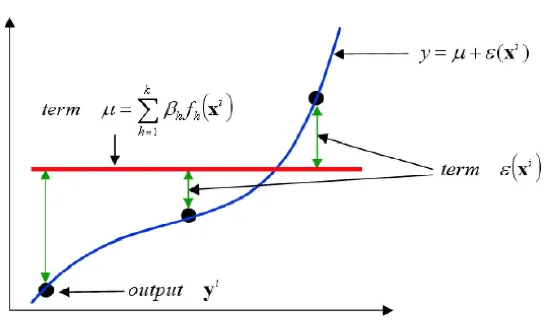
回帰の項を一定値μと置き換えると
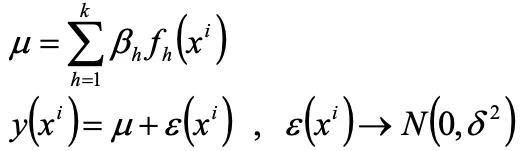
補間モデルを求めるには、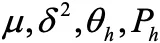
を求める必要があります。
これらのパラメータは下記の尤度関数を最大化することで得られます。（最尤推定法）
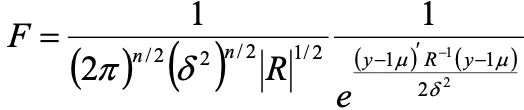
ただし
は下記の近似式を用います。
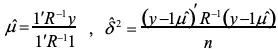
これにより任意の点における応答の推定量を求めることができます。
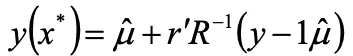
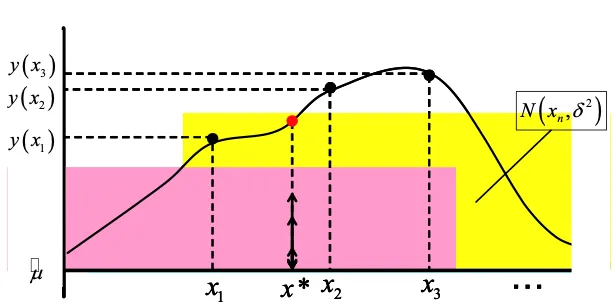
Krigingのアルゴリズムについて
1.定義
- 設計変数の数 k
- 実験点の数 n
- 入力データ x
- 出力データ y
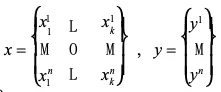
2.相関行列Rの値を求める
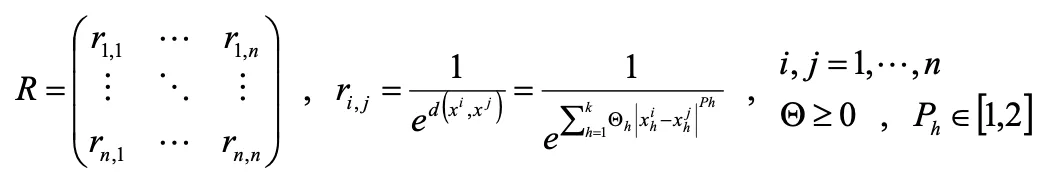
3.相関行列Rの逆行列 R-1を算出する
4.出力値の予測平均値と分散を求める
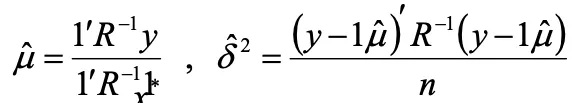
5.任意の点における相関行列Rの r を求める
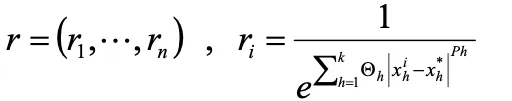
6.任意の点x* における応答の予測値
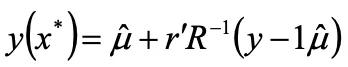
7.任意の点x* における補間誤差
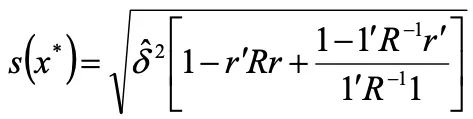
機械学習
機械学習とは、データ分析手法の1つで、データから機械が自動学習を重ねし、データの背景にあるルールやパターンを発見する方法です。ここでは、機械学習の手法についていくつかご紹介します。
ニューラルネットワーク
ニューラルネットワークとは、⼈間の脳にあるニューロンの繋がりを数式的に模倣したネットワーク構造です。多くある機械学習の手法のひとつとして知られており、⼈間の脳をモチーフにすることで、⾼い計算処理能⼒を獲得 し、膨⼤なデータを処理することが可能です。
ニューロンとは？
⼈間の脳はニューロン(neuron)という神経細胞のネットワーク構造となっています。ニューロンから別のニューロンに電気や化学反応のシグナルを発信して情報をやり取りします。
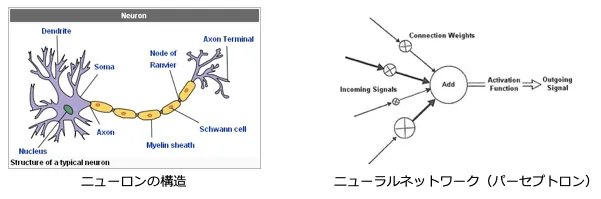
ニューラルネットワークの仕組み
ニューラルネットワークは次の３層から構成されています。
⼊⼒層 - ⼊⼒を与える
隠れ層 - ⼊⼒層からの情報を元に反応し、 結果を出⼒層に 出⼒する
出⼒層 - 結果を出⼒する
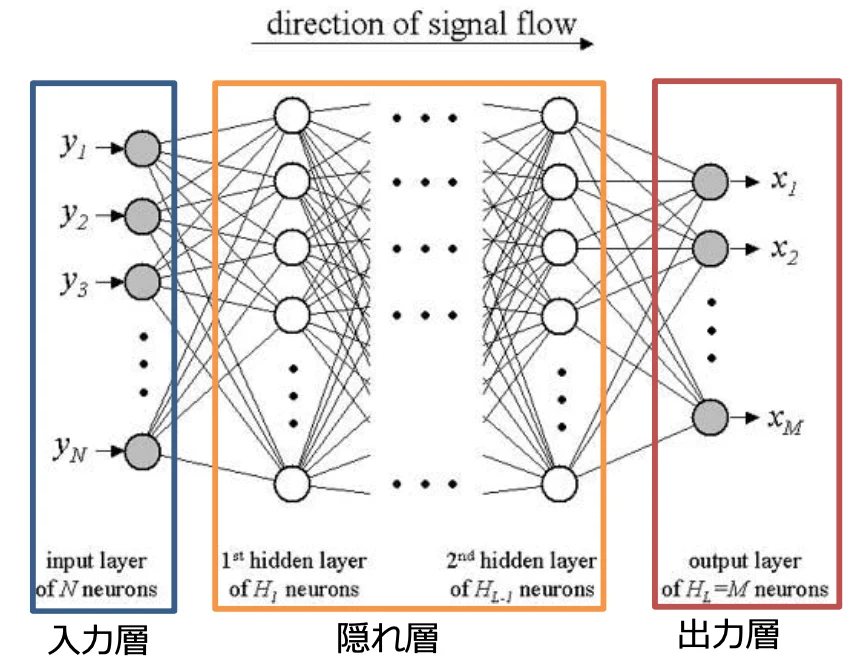
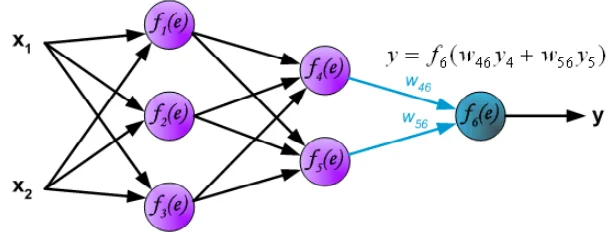
ニューラルネットワークの仕組みは、⼊⼒層から⼊った信号が、隠れ層に含まれる様々な⼈⼯ニューロン（丸の部分）を伝搬して出⼒層に伝わるようになっています。⼈⼯ニューロン同士の繋がりは、「重み」で表されます。
⼊⼒信号に「重み」を乗算して⾜し合わせた値を⼈⼯ ニューロンへ⼊⼒します。⼈⼯ニューロンは⼊⼒値を処理し、他の⼈⼯ニューロンに信号を出⼒します
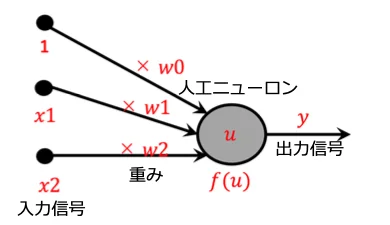
ニューラルネットワークによる出⼒値算出の流れ
①⼊⼒信号x1,x2に「重み」乗算、足し合わせた値を1層⽬の⼈⼯ニューロンに⼊⼒。
人工ニューロンは活性化関数f(x)を用いて⼊⼒値を演算し、y1として結果を出⼒します。
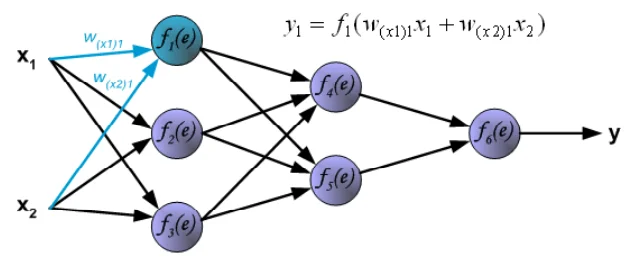
②その他の⼈⼯ニューロンも①と同様に演算を⾏います。
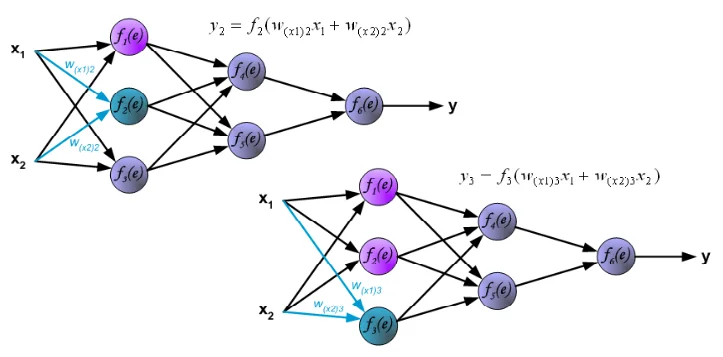
③1層⽬の出⼒値y1,y2,y3に「重み」乗算、足し合わせた値を2層⽬の⼈⼯ニューロンに⼊⼒。⼈⼯ニューロンは⼊⼒値を演算し、y4,y5を出⼒します。
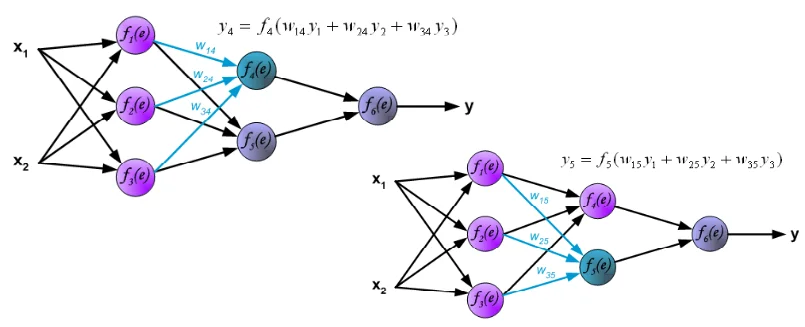
④2層⽬の出⼒値y4,y5に「重み」乗算、足し合わせた値を出⼒層に⼊⼒。出⼒層の演算で得られた結果yが、 ニューラルネットワークの出⼒値となります。
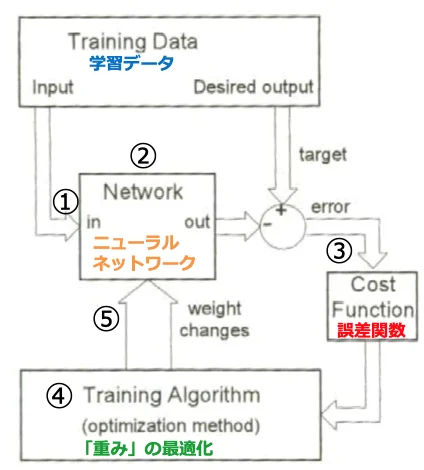
ニューラルネットワークの学習フロー
① 学習データ読み込み。
② ニューラルネットワークを演算し、出⼒値を算出
③ 出⼒と⽬標値（教師データ）との差を表す「誤差関数」を算出する。
④ 誤差関数が⼤きい場合は、出⼒が⽬標値に近づくよう、
アルゴリズムを使用して「重み」を学習（最適化）する。
⑤ 更新した「重み」をニューラルネットワークに適用する。
⇒②〜⑤を繰り返し、誤差関数が最⼩化した場合、 計算を終了します。
ニューラルネットワークは、学習を繰り返すことで、「重み」を 最適化し、解を導くことができます。
RVR (Relevance Vector Regression - 関連ベクトル回帰）
RVR (Relevance Vector Regression) とは、関連ベクトル回帰を意味し、疎な解を持つカーネルモデルの一種です。誤差に強く、汎化性能が高いという特徴があります。サポートベクトルマシンと似た特徴を持つが、サポートベクトルマシンの問題点を克服しています。
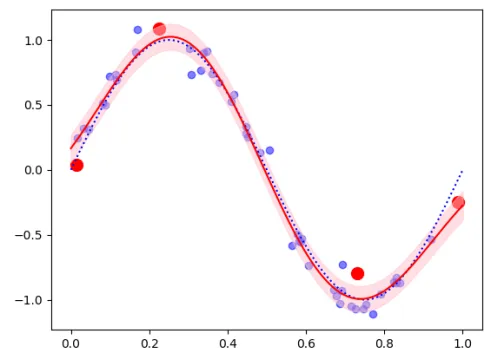
関連ベクトルから作成されたモデル
RVRのメリット・デメリット
メリット
- 原理的に過学習をしない。（※1）
- データが少なく、変数が多くても性能がでやすい
デメリット
- 厳密な計算を行うと計算コストがかかる。 （※1）
※1 近似手法などが使用されるが、近似性能が悪ければ、オーバーフィットやアンダーフィットを引き起こす
RVR作成の流れ
1.モデル構築
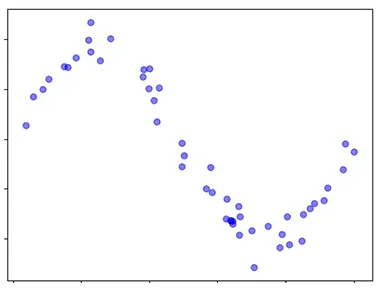
観測データ
- 観測データを再現するモデルを定義
- 事前分布、尤度関数を設定
2.学習
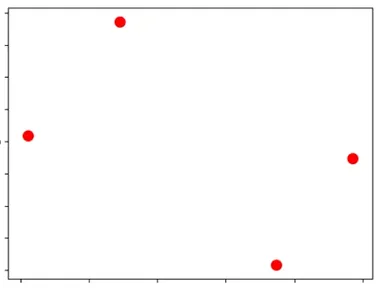
関連ベクトル
事後分布の更新 - 定義に使用したハイパーパラメータαβの最適化
α＊β＊ 最適化後のαβ
関連ベクトル：重みが0ではない入力ベクトルだけが残り、疎なモデルとなる
3.予測
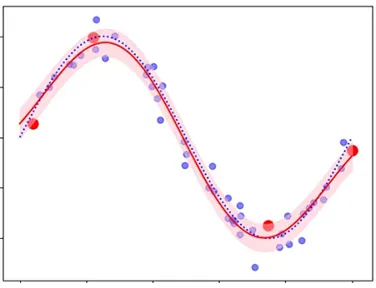
予測モデル（赤線）
最適化したハイパーパラメータを用いた事後分布から予測モデルを作成
RFR（Relevance Forest Regression - ランダムフォレスト回帰）
RFR (Relevance Forest Regression) とは、機械学習手法「Random Forest」をベースとした 応答曲面モデルを作成する手法です。
Random Forest とは
多くの木が集まると「森」になります。RFRモデルはランダムに作成されたサブモデル（決定木）の集合です。
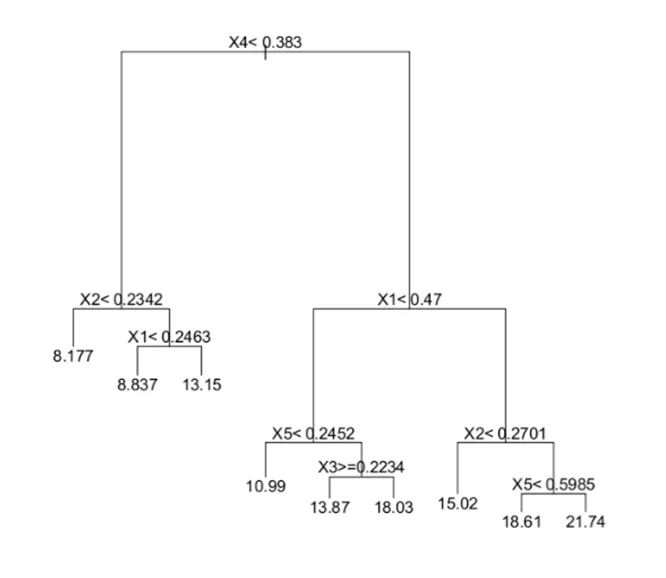
例）5つの変数を持つ決定木
RFRのメリット・デメリット
RFR には以下のようなメリットとデメリットがあります。
メリット
- 設計変数が多くてもモデル作成が高速
- データのランダム選択によりノイズの影響を抑制
デメリット
- 設定によってはオーバーフィッティング
- データ数が少ないと精度の良いモデルができない
RFRのアルゴリズム
① ベースとなるデータセットからランダムにサブセットを作成
② 各サブセットをトレーニングデータとして決定木を作成
③ 決定木の応答曲面モデルを作成しその平均をモデル出⼒
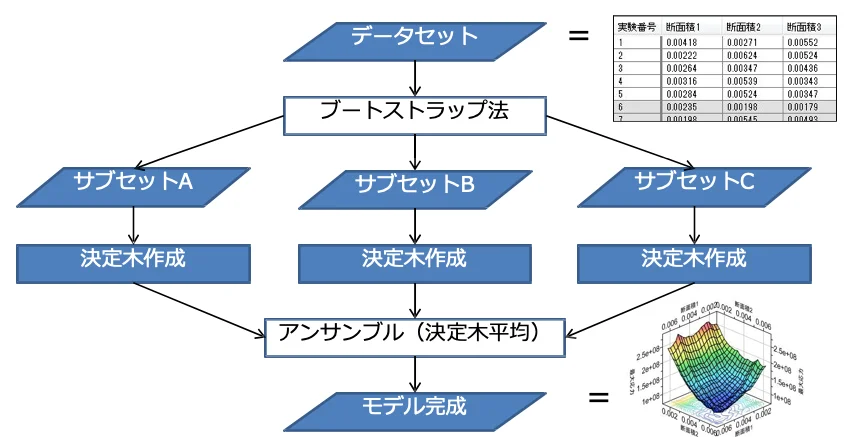
RFRのアルゴリズム
ベースとなるデータセットからランダムにサブセット
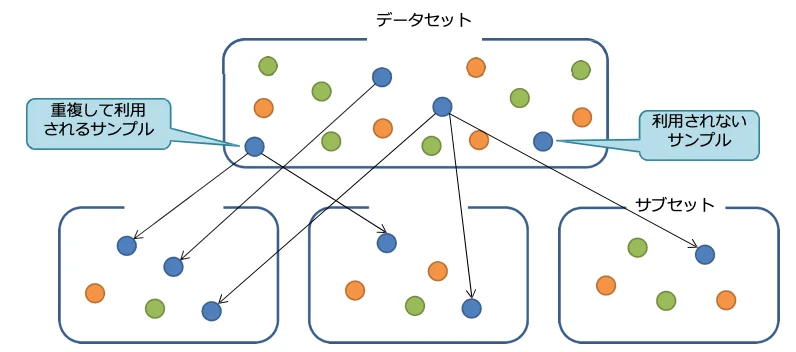
① ベースとなるデータセットからランダムにサブセットを作成
- 作成する木の数だけサブセットを生成します。
- データの選択は完全ランダムです。（ブートストラップ法）
- サブセット間のサンプルの重複を許容
- 学習に利⽤されないサンプルも許容
各サブセットをトレーニングデータとして決定木を作成
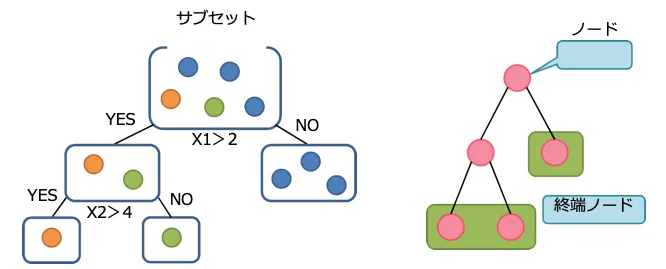
② 各サブセットをトレーニングデータとして決定木を作成
- サブセットを分割する設計変数を幾つかランダムに選択します。
（分割タイプは、ランダム、平均値、中央値、中点から選択可能） - 選択した設計変数毎にランダムに分割し、最適な分割を求めます。
（最適な分割の判断は、予測される平均2乗誤差を使用）
以下の終了判定を満たすまで分割します。- 指定した設計変数の数だけ分割を実施した場合
- 終端ノードのサンプル数が指定した数を下回った場合
③ 決定木のサブモデルを作成し、全サブモデルを平均して応答
曲⾯モデルとして出⼒
- 決定木ごとに、終端ノードで回帰分析しサブモデルを作成
- 全てのサブモデルを平均しモデルを作成
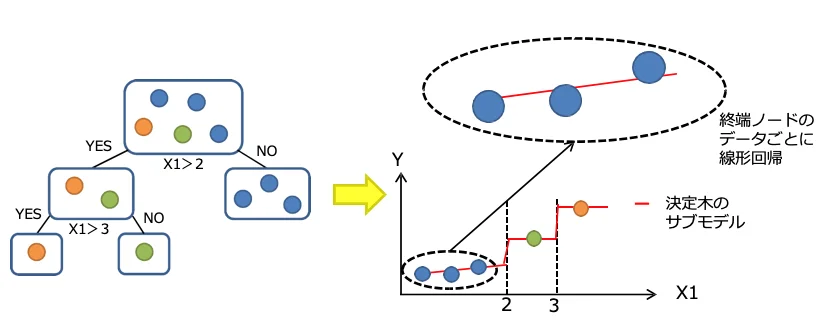
サブモデル作成イメージ
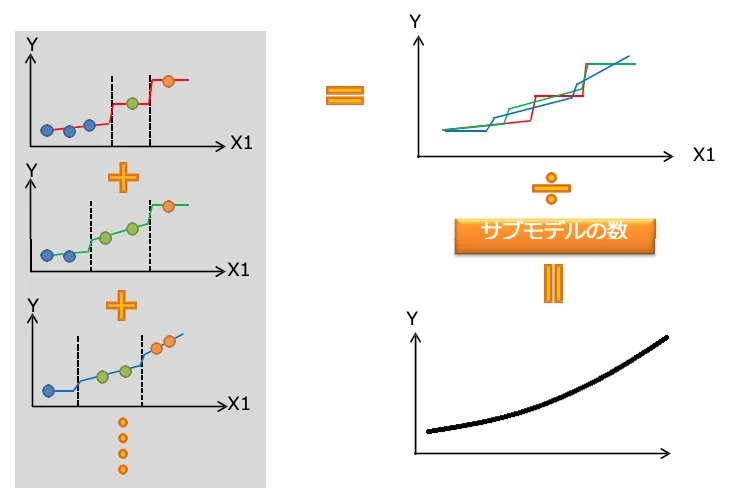
サブモデルを平均し、応答曲面モデルを作成するイメージ
上記の図に示すとおり、決定木（サブモデル）が多いほど応答曲⾯モデルは滑らかになります
Multi-Fidelityモデル
3D CAEや実験データなどは精度の良い結果が得られる反面、データを収集するまでに時間が掛かってしまいます。一方、1D CAEや近似モデルなどは限られた時間内で多くのデータを収集できますが、精度が劣ります。これらの精度が異なる複数のデータ群を基に精度の良い応答曲面モデルを作成する手法がMulti-Fidelityモデルです。「Multi-Fidelity Model」は異なる忠実度のデータを融合することで低コストでも精度を向上した応答曲面モデルを作成する手法です。
データ数は多いが 真の応答とは離れた位置にデータ点やモデル精度が低い「低忠実度データ(モデル)」と、データ数は少ないが真の応答と同じ位置にデータ点がある（ただし、範囲以外のモデル精度が低い）⾼忠実度データを融合して、低コストでも精度を向上した応答曲面モデルを作成します。すべてのデータを考慮するため、単一忠実度モデルよりも優れた精度になります。
実験計画法の関連情報
● 最適設計支援ツール Optimus における「実験計画法」の機能について
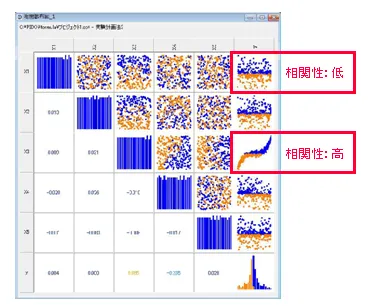
Optimusの実験計画・応答曲面手法は設計パラメータと出力の間で形成される解空間の分析に広く活用することが可能です。最適化を行う前にこれらの手法を通して多くの情報を把握することで、より「効率的な最適化」への指針が導き出されます。また、得られた結果はポスト処理を通してその相関性を視覚的に確認できます。
詳細はこちら>>
● 動画コンテンツ「はじめての最適化」
「CAEを活用した最適化に興味はあるが何から始めて良いかわからない」
「CAEの最適化を使用しているが良い最適解が得られない」とお考えの方を対象に作成した動画コンテンツです。最適化問題の特徴を分析するために実施されているサンプリング手法である実験計画法についてご紹介します。また、問題分析の必要性や、サンプリングについても解説します。
本ページは、応答曲面法の概要や応答曲面法のさまざまな手法についてご紹介しました。CAE 解析をご検討の際は、ぜひ弊社までお気軽にご相談ください。