動解析における加振法 Vol.4
「ラグランジェの未定乗数法」
これまで3回にわたって構造物の加振法について書いてきましたが、今回はそのシリーズの最後としてマニアックというか、ちょっと変わった加振力の定義方法を紹介します。
ラージマス（大質量要素）法は加振する構造物の質量に比べて何倍も大きな質量を定義し、それを加振する手法でした。重い部分を振れば軽い部分も一緒に振動するというイメージは、解析に慣れていない人でも取っ付き易いと思います。強制変位法も通常静解析で強制変位を使っていれば、それを振動させるだけなので、同様にイメージしやすいかと思います。しかし、今回述べる手法は、剛性マトリックスや質量マトリックスなどを直接操作して加振力を与える、極めて数学的な手法になります。FEMに慣れていない人はちょっと理解し難しいかもしれません。
まず簡単な例として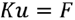
で表される静解析から考えてみましょう。この場合は静解析なので、強制変位を与える場合になります。
ここで(1)式に自由度を1つ加え以下のように定義します。
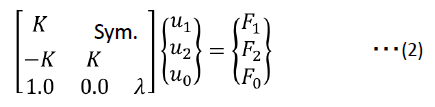
(2)式の第３項から以下の関係を得ます。
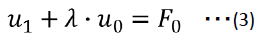
ここで※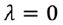
を与えれば、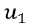
は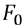
に与えた荷重と同じ値だけ強制変位することになります。すなわち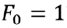
であれば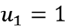
になります。
（※実際は1.0×10-8程度の極小さな値を入れるほうが安定すると言われます。）
こんどは同じことを一般形(n自由度)の運動方程式に当てはめてみましょう。
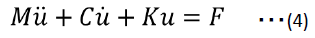
(2)式と同じように自由度を1つ追加します。ただし以下では質量項に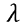
を入れています。
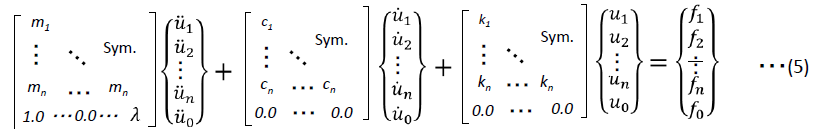
ここで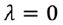を与えれば、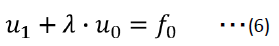
は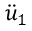
に与えた荷重と同じ値の加速度になります。すなわち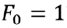を与えれば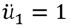
という加速度を定義したことになります。もし(節点1の1方向)ではなく違う方向に加速度を定義したいのであれば、その自由度に対応する項を1.0にすれば良いわけです。同様に質量項ではなく減衰項に上記を定義すれば強制速度を定義することができます。
なぜこのような面倒な手法があるのかと思うでしょうが、宙に浮いている構造物に対する多点加振入力に使えるということでした。ラージマス法や強制変位はベース加振の手法なので、多点で加振すると加振点の拘束の影響を受けます。とは言え、あまり使う人もいないでしょうから説明はこれくらいにします。