CAEコラム
動解析における加振法 Vol.5 「ラグランジェの未定乗数法・続」
前回、あまり使う人もいないでしょうからと、詳しい説明を省いたのですが、一部の方から、もう少し詳しい説明を見たいとのリクエストがありましたので、続編として入力データ例を掲載することにしました。ただしマトリックスの直接入力を行うのにMATRIX27というコマンドを使った入力操作を行うためANSYSのAPDLを使います。最近はWorkbench環境しか使ったことがないという方も増えているため、APDLは全然わからないという方もいらっしゃるかもしれませんが、今回はご容赦ください。またANSYS以外の解析ソフトをお使いの方もいらっしゃると思うのですが、その場合は、お使いのソフトの入力データに置き換えていただけますようお願いいたします。
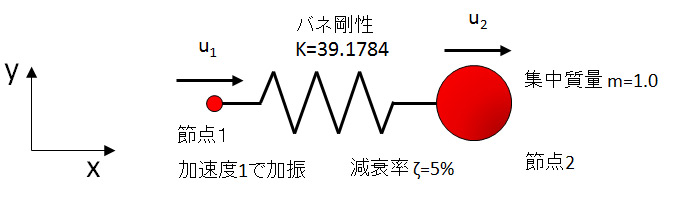
図1 解析モデル
モデルは図1に示す単純な1バネ1マスモデルです。固有振動数が1Hzになるようバネ剛性を定めているため、きりの悪い値になっています。減衰率は5%とするので、節点1を1Gで加振すると節点2はx方向に10Gの応答加速度を生じます。
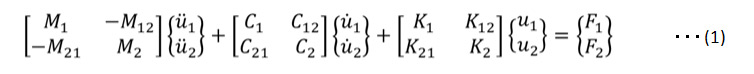
図1に示す系の運動方程式は(1)式です。この式の自由度を追加して(2)式の形にします。この場合節点1に強制加速度を加えたいので λ は質量マトリックスに定義します。
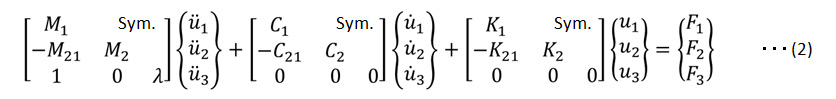
ここで(1)式に対し、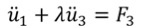
が追加されたことになります。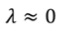
を定義すれば、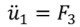
、すなわち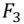
として定義した荷重と同じ値の加速度が節点1に定義されます。
具体的にはANSYSではMATRIX27というマトリックスを直接入力するコマンドを使います。これは任意の節点mと節点nの2節点に対し12×12のマトリックスを定義するもので、質量/減衰/剛性マトリックスのそれぞれに対して可能です。定義には2節点必要なためダミー節点として節点3を定義し、節点1と節点3に対しMATRIX27を定義します。
本例題の場合は加速度マトリックスの項を追加したいため、質量マトリックスの定義オプションを使います。そして節点1のX方向の自由度に対応する項に1.0を入力し、節点3のX方向自由度に対応する項には λの値(ここでは-1.0×10-10)を入れます。その他の項は全て0が入ります。これで節点3のX方向に1の力を加えると節点1のX方向に1(G)の加速度が生じることになります。
図2に入力ファイルのサンプル、および図3に結果出力を示します。
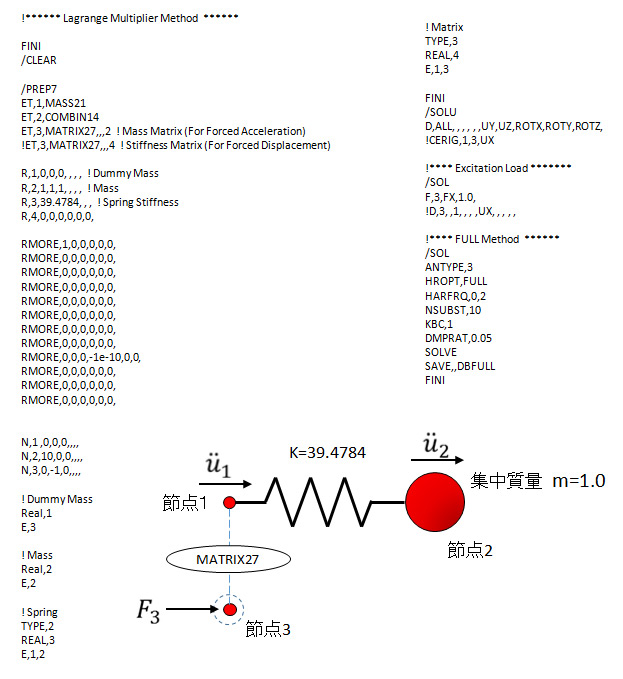
図2 Lagrangeの未定乗数法入力例
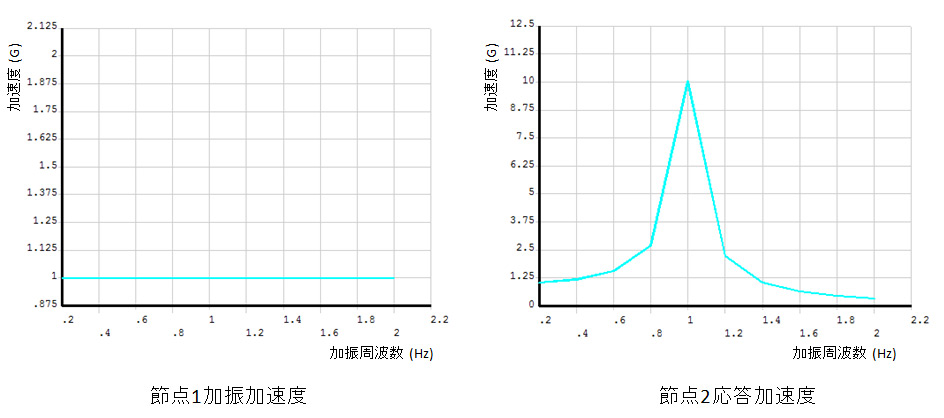
図3 解析結果プロット図





