CAEコラム
動解析における加振法 Vol.1 「ラージマス法」
通常、構造解析では変位/速度/加速度といった拘束条件を直接設定できますが、周波数応答解析では直接拘束が難しい場合があります。
ラージマス法は、周波数応答解析において構造物に加速度の拘束条件を直接設定できない場合の代替として考え出された手法です。
ラージマス法では加速度の拘束条件の代わりにF(ω)、つまり加振荷重を与えることによって構造物を振動させます。
F(ω)を加振荷重、Mを構造物の質量、aを生じる加速度とすると、Mもaも既知なのでF(ω)=Maの関係からF(ω)は決まるのではないか? この構造物が剛体なら良いですが、加振すると構造物は振動します。その影響が加振点へフィードバックされ加振力へ影響を与えてしまうので、結果として入力したはずの力で振れないことになります。
もっとも、一回やってみれば実際はどうなるかがわかるので、その影響を考慮して加振荷重を決め直し、再度解析すれば良いのですが、振動周波数を変えるたびにそんなことをするのは現実的ではありません。 そこでこれを解消すべく、いくつかの加振方法があります。まずはもっともポピュラーと思われる「ラージマス法」です。「大質量法」とも言われるこのやり方ですが、解析モデルはとても簡単で、名前の通り「大きな質量」を加振点に設定し、その質量と同じ値の加振力を定義するだけです。
例えば、ピンポン玉を針金に刺して、反対側を手で持って振ると、ピンポン球が振れる影響が手に伝わるのを感じます。そこでこんどは手で持った側をボウリングの玉にさし(ピンポン球とボウリングの玉が針金を介してつながった状態)、ボウリングの玉を持って振ります。ボウリングの玉につながったピンポン球は振動するのですが、ボウリングの玉が重いので、ピンポン球が振動する影響は手に感じなくなります。
これがピンポン球とゴムボールくらいの差であれば、まだ影響は感じられるかもしれません。しかしピンポン球とボウリングの玉のように相対的に質量の差がとても大きいのであれば、小さい方の質量の影響は無視できますよということです。
ではどれくらい差があれば良いのかということですが「これだ」と決まったものでもなく、106〜1010くらいと言われています。それってものすごい幅があるんじゃないの?ということになりますが、じゃあ1012ではできないのかというとたぶん大丈夫です。何てアバウトな!
あえて書くほどの事はないですが、モデリングイメージは下記です。
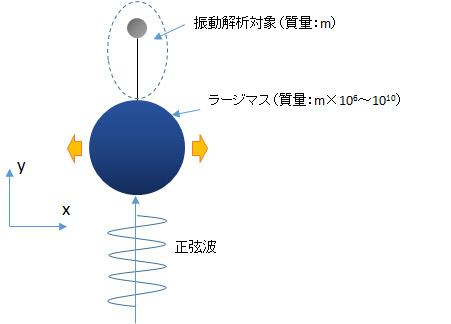
ラージマス法のモデリングイメージ
誰が最初に考えたのか知らないですが、この大雑把さがなんともアナログ的でレトロなイメージがしませんか。その昔CAEを始めた頃に、FEMやコンピュータというデジタルまみれなさっぱり訳のわからない知識に戸惑っている中で、「やたら大きなおもりをくっ付けて揺するだけ」というやり方を知った時に、その発想がなんだかとても面白かったことを思い出します。「細かいことは無視しておけばええんや!」みたいな。
さて、次回は加振点を止めて振動させる方法についてです。





