CAEコラム
「イナーシャリリーフ解析」 CASE2
サイバネットは、エンジニアのための理論教育講座「CAEユニバーシティ」を主催しています。このコーナーではその「特別講座」として、講師の方などに専門分野をわかりやすくご紹介いただきます。
目次
1. CASE 2:重心点以外の場所を拘束して解く方法
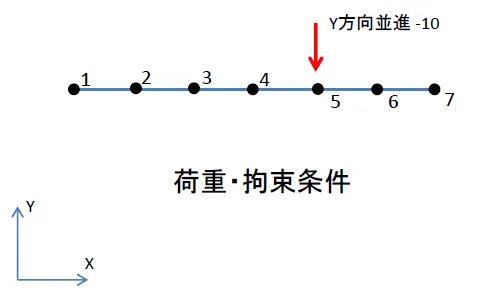
行いたいのは前題と同じ、棒が無重力中に浮いた状態で、節点5にY方向荷重をかけた場合の静解析です。節点4は重心点ですが何かの事情で拘束できないとします。とは言え、拘束がない状態での静解析はエラーになるので、ここでは節点1をピン支持、節点7をローラー支持とする静定構造としてStep1の静解析を行います。
後の考え方は前題とまったく同じで、Step2とStep3で回転加速度と並進加速度をかけ、拘束反力が0になるように荷重ケースの線形和を行えばよいです。
Step1
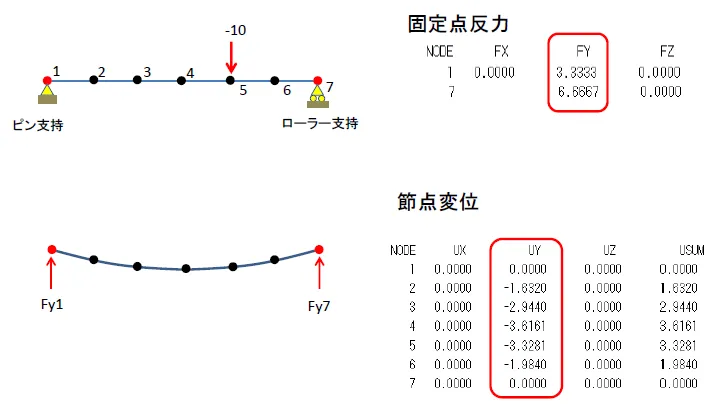
棒を2点で静定支持して静解析を行う。拘束点反力は節点1と7の2か所に生じる。
Step2
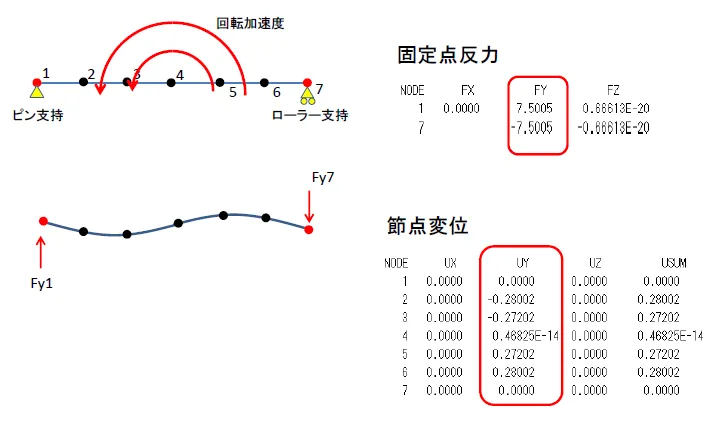
Case1と同様、重心点廻りに回転加速度をかけて拘束点反力を求める。
Step3
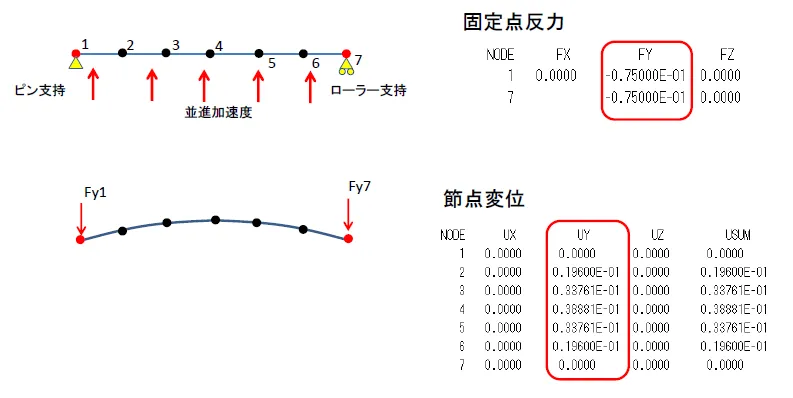
次に並進加速度をかけて拘束点反力を求めます。
2. まとめ
解析結果は以下になります。

これで後はStep1とα*Step2とβ*Step3の足し合わせにおいて拘束点反力が0になるようにαとβを決めれば良いわけです。そうすると以下を得ます。

変形図は以下です。

Case1と変位の値が違うじゃないかという方は傾きを補正して比べてみてください。
以上、2次元のモデルで解析を行いましたが、3次元モデルでも同様にできることがわかります。3次元の場合は3点で静定支持になるように仮の拘束点を定め最初の静解析を行います。次に重心と慣性主軸を求め、重心点において慣性主軸に沿った回転加速度や並進加速度をかけて静解析を行います。そして、最後に拘束点反力がキャンセルして0になるように各荷重ケースの倍率を定めて線形和を求めればよいです。
とは言え考えてみればわかりますが、3次元モデルでこれを手計算で行うのはほとんど不可能です。そこでこの手順をプログラム化して組み込んだものがイナーシャリリーフ機能になります。
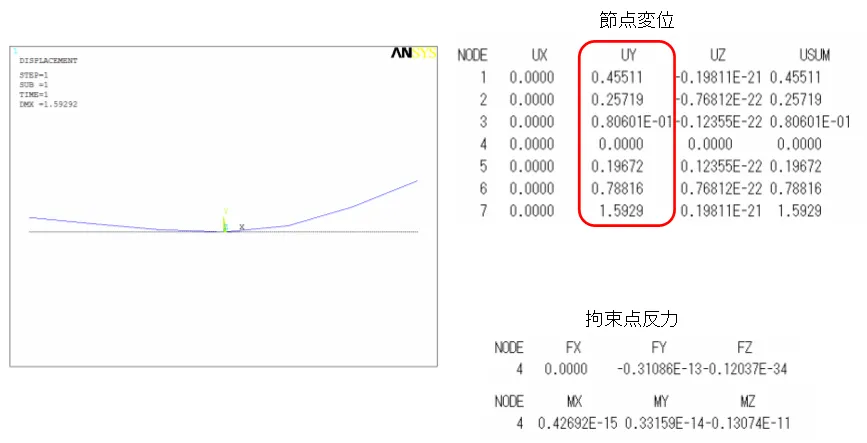
最後に、実際にANSYSでイナーシャリリーフ機能を使って解析した結果を示します。今回Case1で行った結果とよく合っています。