CAEコラム
エンジニア向け理論教育 「CAEユニバーシティ力学系講座が目指すもの」
筆者:東北大学大学院工学研究科 准教授 寺田 賢二郎 先生
目次
はじめに
CAEユニバーシティが開講したのは2007年の秋ですが、当初から「FEM原理」を担当し、サイバネットの担当者と一緒に実習や力学などFEM関連の各講座をコーディネートしてきました。 CAEユニバーシティの内容については、これまでこの「サイバネットニュース」でも何度か紙面が割かれてきたようですので、ここでは「計算力学に基礎を置くCAE」に特化して、大学でいえばカリキュラム策定委員としての立場から、CAEユニバーシティとはどのようなものなのか、どうあるべきなのか、について説明したいと思います。
CAE“ユニバーシティ”の語感
ユニバーシティ”の和訳は、言うまでもなく学術研究および教育の最高機関である“大学”ですが、「CAEユニバーシティ」は、サイバネットという一企業が提供し、研究を主眼としないので、厳密にいえば学校教育法の定める大学とは異なります。また、単独の講座だけ見ると、同社が提供している講習会やセミナーとの区別がつきにくいのも事実です。しかし、少なくとも教育機関としての大学に近い理念を掲げ、同等以上の知識レベルを提供する、新しいかたちのCAE教育システムとして設立されたものであり、(後述するように)“ユニバーシティ”としての語感が保たれるよう配慮されたカリキュラムが提供されています。
「CAEユニバーシティ」の特徴として第1に挙げられるのは、計算力学関連の講座を担当するすべての講師が大学の教員であることです。私たちは、もちろん研究もしますが、講義を通して学識を普及することを使命とする教育者でもあります。そして、私たちのCAEユニバーシティでの教育方針は、大学における学部生・大学院生に対する教育同様に社会人教育を目指しています。学校教育法(第九章 大学)的にいえば「(中略)広く知識を授け(中略)知的、道徳的及び応用的能力を展開させることを目的とし、(中略)その成果を広く社会に提供することにより、社会の発展に寄与する。」という意識で臨んでいます。
そのような教育は本来大学で行うべきではないか、との批判もあろうかと思います。しかし、残念ながら現在の大学の教育システムでは、“CAEによるものづくり”という観点は希薄で、CAEの中枢を担う計算力学・計算工学は学際領域として認識されているものの、従来型の大学教育にはなじみません。すなわち、大学の工学系の学部・大学院のほとんどが、機械・航空・造船・原子力・土木といった近代以降に成立した縦の分野割を堅固に守り続けており、CAEを基調として既存の学問体系を構成し直すことは不可能に近いといえます。ものづくりにおけるCAEが急速に重要度を増している現実がある一方で、大学ではCAEを基調として体系化された教育カリキュラムは提供されないという一種のねじれ現象は、しばらくの間は解消されることはないでしょう。だからこそ私たち講師は、研究・教育面でCAEに携わる大学人として、CAEを体系的に学習できる環境を作ることことに責任を感じており、NPOの活動や、CAEユニバーシティを通してこの分野に貢献したいと考えているのです。
シミュレーション・数値計算・解析
ここでいまさら「CAEとは何か」を述べるつもりはありませんが、CAEの定義に用いられる「シミュレーション」「計算」「解析」という用語の意味を確認しておきましょう。
「シミュレーション」は設計対象に関する物理現象を “模擬する”ことを意味しますが、CAEではその主体(すなわちユーザ)が必要なデータを揃えてソフトウェアを実行すれば、“もっともらしい”結果が出力され、これが正しいものと信じて設計支援を行っています。この際、ソフトウェアの中身は基本的に非公開の場合が多いので、ユーザがこれをブラックボックスとして扱えば、ソフトウェア内部で行われている「数値計算」を無視したことになります。一方、ソフトウェア内部での「計算」を意識することは、計算対象となる「数式」を意識したことと等価です。それによってはじめて物理現象がクリアになり、計算結果に対する分析、すなわち「解析」が可能になるのです。つまり、厳密には「シミュレーション≠解析」であり、「計算の内実=理論」を知らなければ“≠”は“=”になり得ないことになります。
図-1を参照下さい。まずCAEで解析対象とする物理現象は、数学的なモデルに置き換えられます。次にそれがコンピュータで扱うことのできる数値的手法に置き換えられてソフトウェアに実装されます。前者の物理現象の「数理モデル」の具体形は、ほとんどの場合が偏微分方程式であり、初期値と境界条件を合わせて「支配方程式」と呼ばれます。これに対して後者のソフトウェア内にプログラム実装されている数式は「離散化(支配)方程式」であり、その解は一般に厳密には偏微分方程式を満たさない近似解となります。すなわち、CAEソフトウェアの利用により得られる計算結果と実際に起こり得る現象との間には必ず差が生まれます。それらは総称的に誤差と呼ばれ、具体的には以下のようなものが含まれます[1]。
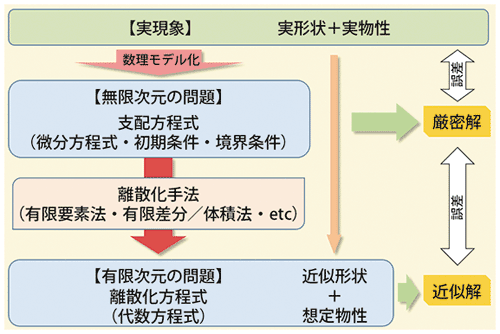
図-1:現象のモデル化・離散化と誤差
(a)物理現象を数理モデルで表すことによるモデル化誤差:支配方程式の正当性
(b)材料データの誤差:構成則のパラメータなど
(c)形状近似の誤差:CAD等の形状モデルから計算モデルへの変換時など
(d)境界条件の設定による誤差
(e)離散化誤差:要素、メッシュ分割方法等
(f)丸め誤差:コンピュータの浮動小数点の表現性能
(g)結果の可視化等の出力に際して介入する誤差
計算結果にはこれらの誤差が含まれることを認識し、以下のような意味での「数式の理解」がなければ、シミュレーションはできるかも知れませんが、解析はできたことになりません。
(1)元の支配方程式とその解の特性
各変数およびパラメータの物理的意味、初期・境界条件と微分方程式の型など。
(2)離散化支配方程式とその解の特性
元の支配方程式がどのような方法で離散化方程式に変換されているか。その離散化方程式の解はなぜ近似解なのか。それはどんな近似で、どの程度の誤差が含まれるのか、など。
CAEユニバーシティは、これらを学習するための講座群の総称であり、このような意味での「解析」ができる人材を育成するためのカリキュラムを編成しています。
CAE教育カリキュラム
前述のように、CAEユニバーシティでは大学教育のシステムに倣って「ある一定の基準に照らして策定されたカリキュラム」を提供しているという点で、通常の講習会やセミナーとは異なります。すなわち、各講座は互いに有機的に関連し合っており、学習する内容は、できる限り重なりのないよう、また不足のないよう吟味されています。実際、計算力学関連の講座を受け持つ講師は、不定期的ですがカリキュラムミーティングを開催して講座間の相互関係を確認・修正しています。
現在のところ、CAEユニバーシティにおける計算力学関連の講座は、図-2に示す基礎講座、専門講座および実習から構成されています。各講座は、開講に際して達成目標と受講要件が示され、かつ講座間の相関も明示されているので、受講者が自身の持っている知識と照らして、どの講座を受講すべきか、あるいはどのような順番で受講していくべきか判断しやすくなっているはずです。
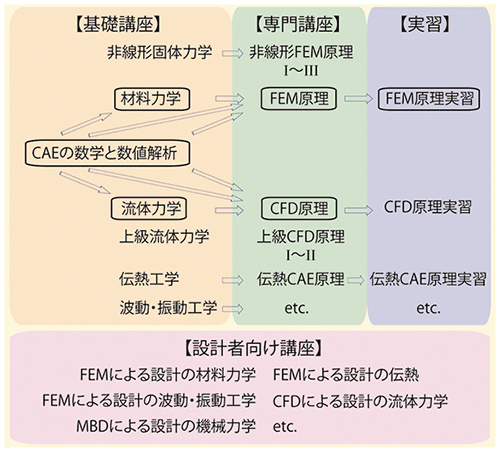
図-2:CAEユニバーシティの構成
(□で囲まれた講座・実習は既に開講中。その他は計画中あるいは開講予定)
計算力学・計算工学に関連したCAE教育のためのカリキュラムとしては、熱工学、波動・振動、各種非線形問題と、それぞれの問題に対する数値計算法などの講座が必要ですが、今のところはまだ計画の段階です。これらが整ってきたところで、以下のようなコースを設定して、よりシステマティックで柔軟なカリキュラムへの移行が望ましいと考えています。
(1)固体の解析者コース
(2)流体の解析者コース
(3)熱の解析者コース
(4)振動・波動の解析者コース
(5)設計者コース
ここで、(1)〜(4)のコースは、現象の支配方程式、離散化方程式、近似特性という順に学習するもので、現在開講されている講座を拡充する形になります。一方、(5)の「設計者コース」は設計者向けの教育プログラムとして新たに設置するもので、CAEソフトウェアを用いて現象を再現し、その現象とその数理モデル(支配方程式)に関する理解を深めることを第一目標とし、離散化や近似特性の細かい式展開については従属的に学べるような講座を考えています。例えば、「CAEで学ぶ設計の力学」では、設計評価に関連した力学問題に対して、数式から入るのではなく、まずCAEソフトで解いてみて、現象の把握に何が必要かを認識した上で、対応する数式の構造・意味を学び、力学的洞察力を培うといったものです。これは、CAEユニバーシティならではのコース設定であり、一部は試験的な開講を予定しています。
おわりに
CAEソフトウェアに内包されている数式と数値計算を理解することは、支配方程式そのものに加えて、離散化方程式とその特性を理解することです。数値シミュレーションの結果が“もっともらしい”だけでは設計者に対して責任を果たしたことにはならず、どんな式を、どのような方法で、どのようなデータで解いたのかを、しっかりと認識したうえで、計算結果の分析を行うことで始めてものづくりの現場、設計に役立つ「解析」ができたことになります。CAEユニバーシティでは、そのような意味での「解析」のための理論を学ぶ場です。未だ、発展途上ですが、CAEによるものづくり技術者の育成を通して産業界に貢献するという目標を達成するために、受講者と講師とが一緒になってCAE“ユニバーシティ”を形作っていくことができれば幸いです。


