「FEM実験室」

2．理論背景を理解したシミュレーションを実施するまでの道のり

「実際の現象」からCAEソフトウェアでの「解析モデル」に至るプロセスの詳細は前号のサイバネットニュース［1］で説明されているので、ここでは簡潔に以下のように大きく二つに分類します。

（1）物理モデルの構築（数理モデル化）：
実際の現象をうまく表現できる数理モデル（一般には偏微分方程式）を構築するプロセスで、主に物理的な知識が必要。

（2）解析モデルの構築（ソフトウェア）：
数理モデルをコンピュータで取り扱える離散的な方程式に置き換えるプロセスで、主に数学的な知識が必要。

実際のCAEのプロセスに置き換えると、前者は「どのような物理モデルを採用するか？」に対応し、例えば静的解析／動的解析、線形解析／非線形解析、材料モデルの選択などが該当します。これに対して後者は、「CAEソフトを使ってどのように現象を具現化するか？」に関する検討であり、要素選択やメッシュ分割に対応します。

これまでに開講してきたCAEユニバーシティにおける力学系講座、もしくは学協会などが開催するFEMの基礎理論に関する講習会では、理論解（厳密解）と呼ばれる微分方程式の解と比較して解析の精度を議論することが殆どでした。これはまさに後者のプロセスであり、一般に知られている「FEMのメッシュを細かくすると厳密解に収束する」、或いは、「応力集中部ではメッシュを細かくする」というのがその典型でしょう。しかしながら、これらを理解するためには微分方程式の近似解法としての有限要素法を学習しなければならず、シミュレーションの対象となる物理現象に対する「数式による理解」が必要となります。つまり、現象に対する物理的な理解はもちろんのこと、微分や積分更には行列演算などの数学の知識を、フル活用しなければなりません。ところが、このような内容は現役の大学生や大学院生でも難儀しているのが現実であり、日常業務でCAEに携わっているエンジニアが「勉強しよう」と腰を上げるだけでも、大変なモチベーションが必要になることは容易に想像できます。

「もう少し勉強すべき要点が絞り込めれば」或いは、「もっと明確な動機付けがあれば」、CAEの理論体系を勉強してみようと思って頂けるのではないか。そう考えて、実験からCAEの理論体系に興味を持てるような講座として、「FEM実験室」を企画しました。CAEソフトウェアをある程度ブラックボックスとして利用するのは仕方ないこととして、前述（1）のプロセス（物理モデルの構築）を中心に「現象を再現するためにはどのような物理モデルが必要か？」という点から説明を行っています。もちろん、CAEユニバーシティ力学系講座のスピン・オフとして企画したので、最終的にCAEの基礎理論に対する理解が必要だという点には変わりありません。ある現象を表現するためには、○○という物理モデルが必要だけど、その理論背景は？という流れで「勉強する」モチベーションを高めて頂こうと考えています。

3．解析結果に自信を持つために

ANSYSを始めとする現在市販されているCAEソフトウェアでは、入力データさえ用意できれば「もっともらしい」解析結果を簡単に出力することができます。自身の解析結果に自信を持ち、結果の「もっともらしさ」を客観的に説明するためには、どのような物理モデルのどのような方程式を、どのような方法で、どのようなデータを使って解いたのか、などをしっかりと認識して説明できなければなりません。CAEユニバーシティでも、このような疑問に答えられるような人材育成を目指していることは、既に説明した通りです。「FEM実験室」では、「ベリフィケーションとバリデーション」という視点を参考にして内容を構成しました。

近年、計算力学に関する研究分野では、「シミュレーションの正しさ・妥当性をどうやって検証するか？」という議論が行われており［2］、そこで提唱されている視点が以下の二つです。

（1）バリデーション（Validation）
主に物理的な観点から「正しい方程式を解いていますか？」という検証。

（2）ベリフィケーション（Verification）
主に数学的な観点から「方程式を正しく解いていますか？」という検証。

お気づきでしょうか？ 実は、冒頭で紹介した「実際の現象」からCAEソフトウェアでの「解析モデル」に至るプロセスは、この二つの視点を意識して分類しました。

既に説明した通り、後者はCAEソフトの「使い方」や有限要素法の基礎理論に対応し、「FEM原理講座」や「FEM原理実習」で詳しく取り扱っている内容です。これに対してバリデーションは、CAEソフトウェアの「使い道」に対応する観点で、現在の物理モデルが対象とする実現象のシミュレーションを行うために適切であるか、或いはどのような物理モデル（或いはそれに対応したCAEソフトウェアの機能）を利用すれば良いのかを議論します。バリデーションは常に現象とセットで考えなければならないため、実際に実験を行って、その結果と対比しながら妥当性を検討する「FEM実験室」で取り扱うテーマとして最適です。

シミュレーションの特徴は「モデル化の際に考慮していない現象は絶対に現れない」という点です。極端な例ですが、線形弾性体を仮定した物理モデルを使っている限りは、その応答が非線形になることはありません。何らかの弾塑性モデルを採用しなければ、金属の応力・ひずみ関係が非線形になる応答は表現できませんし、大変形のオプションをONにしなければ大変形や回転の効果は再現できないのです。当たり前のように感じるかもしれませんが、こうやって必要な物理現象（モデル・機能）を一つずつ追加する「足し算」のプロセスがまさにシミュレーションのバリデーションなのです。注意しなければならないのは、バリデーションはパラメータ・チューニングやキャリブレーションとは異なるという点です。新しい物理モデルやCAEソフトウェアの機能を追加するためには、そのモデルがどのような効果を表現するために構築されたものなのか、或いはその機能をソフトウェアに実装するためにどのようなアルゴリズムが採用されているのかを把握しなければ、狙った効果を正しく反映させることはできませんし、単なるパラメータ・チューニングに陥ってしまいます。

現在の「FEM実験室」（Ver.1, 2）では、図-1のような薄板に対する4点曲げ、および両端をクランプで完全に固定した曲げ実験を対象としています。4点曲げの実験を試験片物性値のキャリブレーション対象として解析モデルのベリフィケーションを行ったのち、ここで同定した物性値を使って両端を固定した曲げ試験のシミュレーションに挑戦します。現象が単純なだけに、簡単にごまかすことはできません。実験を行ってバリデーションの比較対象となるデータを取得するのも、その結果とシミュレーションを比較して「何が足りないのか？」を考えるのも参加者の皆さんです。実験結果がおかしいと感じれば条件を整えて再実験しても構いませんし、「何が起きているのか？」を把握するために条件を変えた実験を行って頂くことも可能です。

4．FEM“実験室”の語感

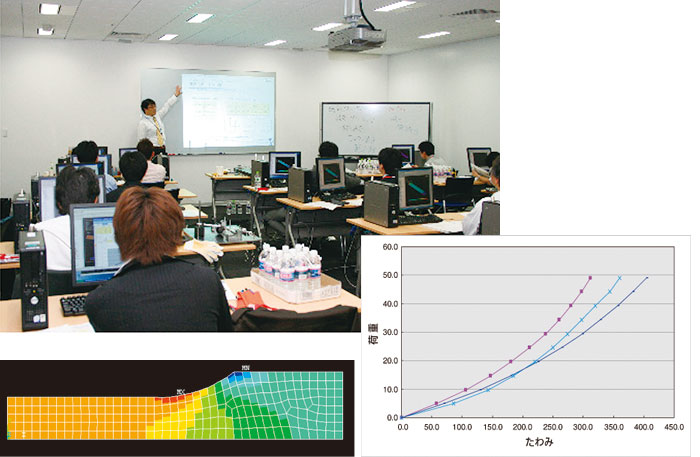
もともと、解析と実験の融合した講座であることを意識して「実験室」と名付けて開講し、ベリフィケーションとバリデーションという概念だけでなく、それを実現するためには実際の現象を手にして考えることが大切であることを伝えてきました。これまでに8回開催し、多くの参加者と議論させて頂くうちに、“実験室”の持つもう一つの可能性に気づきました。「FEM『の』実験室」です。

現在は講師が事前に用意したストーリーに沿って進めていますが、必ずしもそれが正解で、それが全てとは限りません。実際、「○○も考えられるのではないか？」というご提案を頂き、その場で議論が盛り上がった回もありました（議論が白熱して終了時刻までに予定していた内容全てが終わらなかったのは言うまでもありません）。バリデーションの第一歩が「物理現象を素直に見つめること」であるとすれば、参加者それぞれが、「どのような観点で現象を把握してシミュレーションを行ったのか？」という情報を持ち寄って、情報交換やディスカッションの場として「FEM『の』実験室」を企画しようと検討しています。

5．おわりに

いかがでしょうか？漠然とCAEの基礎理論を勉強しようとすることに比べれば、モチベーションや目的・範囲が明確になりませんか？

おそらくバリデーションにはゴールがなく、「FEM実験室」も発展途上ではありますが、受講者の皆さんと一緒に議論を重ねながら完成形に近づけていきたいと思っています。現在の「FEM実験室」では静的な曲げ問題だけを取り上げていますが、動的な問題や固有振動解析などに対するご要望が多いのも事実です。これらについても「FEM実験室」Ver.3或いはVer.4として取り上げていきたいと考えていますので、ご要望・ご意見などをCAEユニバーシティ事務局宛に頂ければ幸いです。