CAEコラム
CAEユニバーシティ特別講座 ナノスケールサーボ制御 第2回 「HDDベンチマーク問題で学ぶハードディスク装置のシーク制御」
筆者:宇都宮大学 大学院 工学研究科 准教授 平田 光男 先生
サイバネットは、エンジニアのための理論教育講座「CAEユニバーシティ」を主催しています。このコーナーではその「特別講座」として、講師の方などに専門分野をわかりやすくご紹介いただきます。
目次
はじめに
前回,ハードディスク装置(以下,HDD)のヘッド位置決め制御には,大きく分けて,トラック間を高速に移動するシーク制御と,トラック中心に精度良く追従するフォロイング制御があることを説明しました。シーク制御では,制御対象の機械共振を励起せずにいかに速く目標のトラックに到達させるかが特に重要で,フォロイング制御では,制御対象の変動に対して常に安定性を保ちつつ,トラックに高精度に追従することが特に重要になります。そして,それぞれに対して,さまざまな制御手法が提案され,性能の向上がはかられてきました。本稿では,シーク制御の一手法について,HDD ベンチマーク問題によるシミュレーション結果を示しながら具体的に解説したいと思います。
シーク制御の難しさ
ヘッドアームを駆動するボイスコイルモータ(VCM: voicecoil motor)の発生トルクからヘッド位置までの特性は図1に示すように数kHz付近に多数の共振モードを持ちますが,もし,ヘッドアームが完全に剛体として振る舞うならば,最大加速したあとに最大減速をする,いわゆる,bang-bang入力(以下,BB入力)が最短時間での位置決めを達成することが知られています。HDDの制御対象をHDDベンチマーク問題のパラメータを用いて次式で示す二重積分モデルで表現し

BB入力を求めたのが図2です。上段に時間応答,下段にその周波数成分(スペクトル)を示しています。この入力は,10trackの距離を,20ステップで移動するフィードフォワード入力になっています。HDDベンチマーク問題では,1trackは254nm,サンプリング周期は37.9μsと定義されていますので,2.54μmの距離を約0.75msで移動する位置決め制御問題を考えていることになります。
BB入力を図1の制御対象に加えると,図5のように,目標トラック付近で大きく振動してしまいます。通常,トラック幅の±10%以内に収まる必要がありますので,この場合,2msを過ぎてもシークが終わらないことになります。なお,図5は図1に示されている9個の変動モデルすべてに対するシーク応答を示しています。
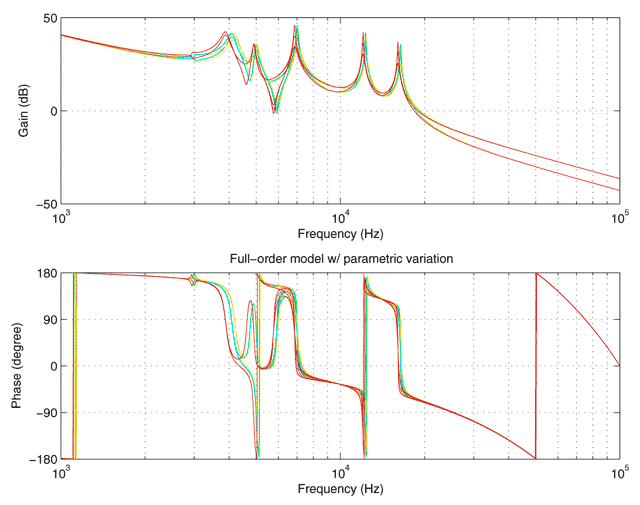
図1: 制御対象のボード線図(HDDベンチマーク問題)
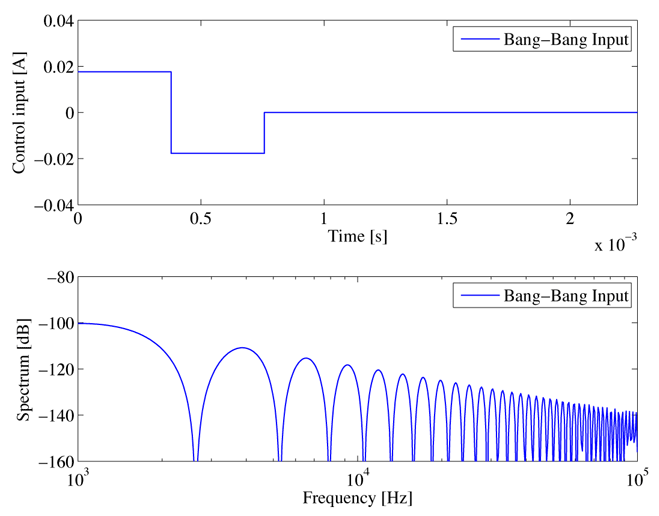
図2: Bang-bang入力とそのスペクトル
ジャーク最小入力
急激な加減速を持つBB入力では,目標トラックの近くには短時間で到達するものの,制御対象の共振モードによる残留振動が大きく,位置決め時間が長くなってしまいます。そこで,入力を滑らかにして残留振動を抑えるために,加速度の1階微分に相当するジャーク(jerk)の2乗積分値を最小としたジャーク最小入力が知られています。
ジャーク最小入力を求めるために,(1) 式をサンプリング周期τでゼロ次ホールド離散化して離散時間モデルPnd[z] を求めたあと,図4に示すように,離散時間の積分器1/(z−1)で拡大系を作ります。すると,拡大系への入力u[k] がジャークになります。次に,拡大系を状態方程式で表します。
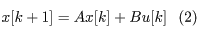
そして,初期状態x[0] を終端状態x[N] までN ステップで到達させる入力u[0], u[1], . . . , u[N −1] を求めることを考えましょう。(2) 式に対してu[k] をk = 0からN − 1まで順次代入してゆくことで,次式が得られます。

ただし
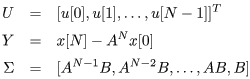
(3) 式はU に関する連立方程式になっており,拡大系が可制御で,ステップ数N が拡大系の次数よりも大きければ,無数解を持つことが簡単に示せます。
そこで,(3) 式を満たすU の中から,ジャーク最小入力を求めましょう。このような入力は,評価関数を

と定義して,(3) 式のもとでJ を最小化することで得られます。ここでは,(4) 式の評価関数をより一般化して,任意の正定行列Q に対して,U に関する2次形式で定義される次の評価関数J を考え,これを最小にする入力を求めてみましょう。

上式は,Q = I と選べば(4) 式に一致しますので,ジャーク最小入力のための評価関数を含みます。
(3) 式のもとでJ を最小化するために,ラグランジェの未定乗数ベクトル2λ を用いてラグランジェ関数を
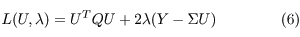
と定義します。そして,∂L/∂U = 0から
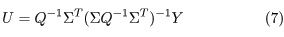
を得ます。このようにしてU を求める手法は,終端状態制御(FSC: final-state control)と呼ばれます。
それでは,図4の拡大系にFSCを適用し,Q = I とおいてジャーク最小入力を求めてみましょう。このとき,U から求まる入力u[k] はジャークですので,実際の入力uc[k]は,それを1/(z −1) で積分する必要があります。得られたジャーク最小入力とそのスペクトルを図3に示しますが,入力の時間変化が滑らかになり,図2にくらべて高周波域でスペクトルも小さくなっていることがわかります。ジャーク最小入力を用いたシーク応答を図6に示しますが,BB入力に比べて残留振動が低減しています。
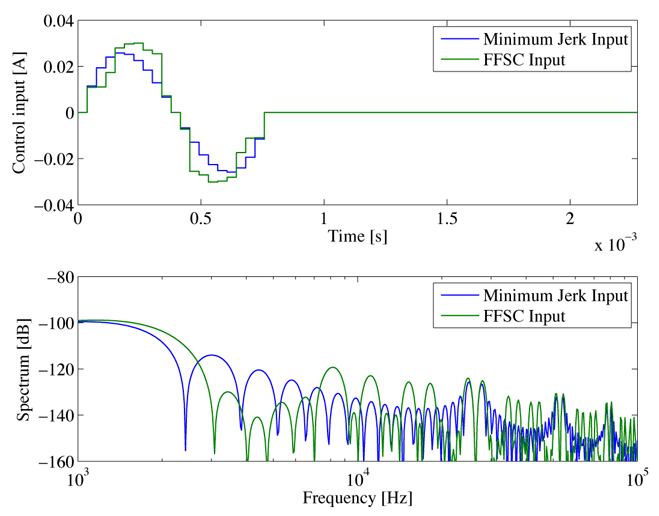
図3: ジャーク最小入力及びFFSC入力とそのスペクトル
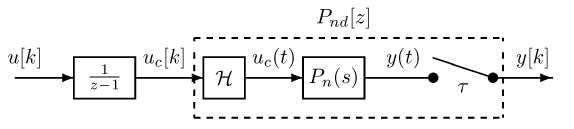
図4: 拡大システム
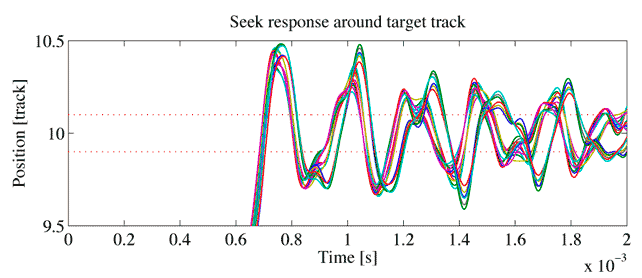
図5: Bang-bang入力によるシーク応答
周波数整形型終端状態制御
ジャーク最小入力により残留振動が低減できましたが,目標トラックの±10%の範囲で,まだ大きく振動しています。そこで,より直接的に残留振動を抑えることを考えましょう。
一般に,制御入力に共振モード付近の周波数成分が含まれなければ,共振モードは励起されません。そこで,制御入力の周波数成分を直接整形することを考えて次の評価関数を導入します。
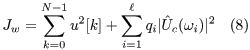
ただし,Uˆc(ωi) は,角周波数ωi における入力uc(t) のフーリエ変換を表し,次式で定義されます。
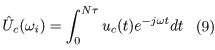
Jw の第1項はジャーク最小入力と同様に滑らかな入力を生成するための項で,第2項はuc(t) の周波数成分を評価する項です。uc(t) は図4の拡大系におけるゼロ次ホールドHの出力ですので,実際の制御対象に加わる連続時間入力の周波数成分を評価しています。第2項のωi を制御対象の共振周波数にあわせて選べば,その周波数成分が低減できます。なお,qi は正の重み定数であり,大きな値に選ぶほど,その周波数成分をより低減できます。
(8) 式は,時間領域と周波数領域の両方の評価を含んだ複雑な評価関数に見えますが,簡単な計算から,Jw = UTQwUのように,U の2次形式で表現することができます。したがって,Jw を最小にする入力は(7) 式から簡単に求まります。なお,(8) 式のもとでのFSCは,周波数整形型終端状態制御(FFSC: frequency-shaped final-state control)と呼ばれています。
図3に制御対象の共振周波数付近の周波数成分を低減するように求めたFFSC入力とそのスペクトルを示します。ジャーク最小入力に比べて,共振モードが存在する3kHz〜7kHz付近のスペクトルが低減されていることがわかります。また,時間応答を見ても,加速開始付近や減速終了付近の応答がより滑らかになっていることもわかります。図7にFFSC入力を用いたときのシーク応答を示しますが,図6に比べて,残留振動が大幅に低減しています。目標トラックの±10% に収まる時間から定義されるシーク時間も1.125msから0.667msと大幅に向上しています。
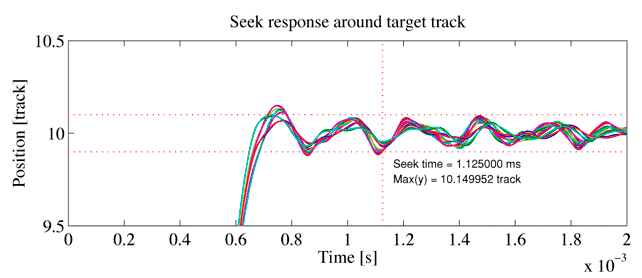
図6: ジャーク最小入力によるシーク応答
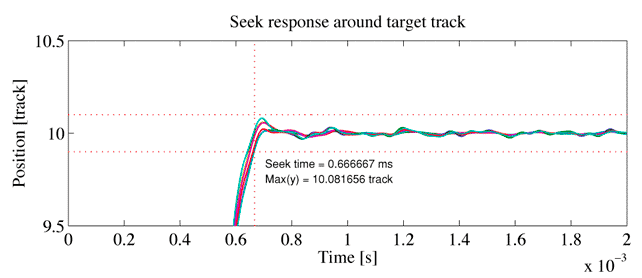
図7: FFSC入力によるシーク応答
おわりに
本稿ではHDDのシーク制御について解説しました。ここで紹介した手法は,入力が飽和しない短距離のシークに向いています。なお,フィードフォワード入力だけでは,外乱に対して脆弱であるため,実際には2自由度制御と共に用いられます。一方,長距離シークの場合は,入力の飽和を考慮する必要があり,また別の手法が用いられます。詳細については,文献1) をご覧下さい。FFSCの解説において,紙面の制約から紹介できなかったQw を求める公式についても詳しく述べられています。また,付録のCD-ROMには,FFSC入力を求めるためのMATLABプログラムが収められていますので,是非お試し下さい。





